Статические и динамические системы

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2

Тема: Системная характеристика объекта динамической системы

Продолжительность занятия 2 часа

1. Цель работы: Закрепить теоретические знания по системной методологии описания экономического объекта и самостоятельно научиться использовать системный подход при описании динамической системы.

2. Вопросы, рассматриваемые на занятии:

1. Рассмотрение теоретических понятий и определений: состояние системы, состояние системы и его оценка, процесс, статические и динамические системы, функция системы, функционирование системы, состояние функции системы, режимы динамической системы, пространство состояний, устойчивость динамических систем.

2. Задачи самостоятельной работы.

3. Оформление отчета по практическому занятию. Отчет выполняется в текстовом процессоре WORD. Обязательное оформление титульного листа отчета. Отчет сохраняется в каталоге «Мои документы» и файловом сервере по указанию преподавателя.

3. Контрольные вопросы:

Поясните, что такое:

a) состояние системы,

b) состояние системы и его оценка,

c) процесс,

d) статические и динамические системы,

e) функция системы,

f) функционирование системы,

g) состояние функции системы,

h) режимы динамической системы,

i) пространство состояний,

j) устойчивость динамических систем.

A. ТЕОРЕТИЧЕСКИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ [1]

Состояние системы

В общем случае значения выходов системы зависят от следующих факторов:

- значений (состояния) входных переменных;

- начального состояния системы;

- функции системы.

Отсюда вытекает одна из наиболее важных задач системного анализа – установление причинно-следственных связей выходов системы с ее входами и состоянием.

Состояние системы и его оценка.

Понятие состояние характеризует мгновенную «фотографию», временной «срез» системы. Состояние системы в определенный момент времени — это множество ее существенных свойств в этот момент времени. При этом можно говорить о состоянии входов, внутреннем состоянии и состоянии выходов системы.
Состояние входов системы представляется вектором значений входных параметров:
X = (x₁,…,x_n) и фактически является отражением состояния окружающей среды.
Внутреннее состояние системы представляется вектором значений ее внутренних параметров (параметров состояния): Z = (z₁,…,z_v) и зависит от состояния входов Х и начального состояния Z₀:

Z = F₁(X,Z₀).

Пример. Параметры состояния: температура двигателя автомобиля, психологическое состояние человека, изношенность оборудования, уровень квалификации исполнителей работы.

Внутреннее состояние практически не наблюдаемо, но его можно оценить по состоянию выходов (значениям выходных переменных) системы Y = (y₁…y_m) благодаря зависимости Y= F2(Z).

Выходные переменные в широком смысле рассматриваются как координаты, отражающие состояние системы и могут выступать не только сами выходные переменные, но и характеристики их изменения – скорость, ускорение и т. д.

Таким образом, внутреннее состояние системы S в момент времени t может характеризоваться множеством значений ее выходных координат и их производных в этот момент времени:

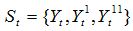
Пример. Состояние финансовой системы России можно характеризовать не только курсом рубля к доллару, но и скоростью изменения этого курса, а также ускорением (замедлением) этой скорости.

Однако необходимо заметить, что выходные переменные не полностью, неоднозначно и несвоевременно отражают состояние системы.

Примеры:

- У больного повышенная температура (у > 37 °С), но это характерно для различных внутренних состояний.

- Если у предприятия низкая прибыль, то это может быть при разных состояниях организации.

Процесс

Если система способна переходить из одного состояния в другое (например, S1→S2→S3…), то говорят, что она обладает поведением – в ней происходит процесс.

В случае непрерывной смены состояний, процесс Р можно описать функцией времени: P=S(t), а в дискретном случае — множеством: P = {St1 St2….}:

1) По отношению к системе можно рассматривать два вида процессов:
внешний процесс – последовательная смена, воздействий на систему, т. е. последовательная смена состояний окружающей среды;

2) внутренний процесс – последовательная смена состояний системы, которая наблюдается как процесс на выходе системы.

Дискретный процесс сам может рассматриваться как система, состоящая из совокупности состояний, связанных последовательностью их смены.

Статические и динамические системы

В зависимости от того, изменяется ли состояние системы со временем, ее можно отнести к классу статических или динамических систем.

Статическая система – это система, состояние которой практически не изменяется в течение определенного периода.

Динамическая система – это система, изменяющая свое состояние во времени.

Итак, динамическими будем называть такие системы, в которых происходят какие то изменения со временем. Имеется еще одно уточняющее определение: система, переход которой из одного состояния в другое совершается не мгновенно, а в результате некоторого процесса, называется динамической.

Примеры:

1. Панельный дом — система из множества взаимосвязанных панелей — статическая система.

2. Экономика любого предприятия — это динамическая система.

3. Учебная группа студентов — это динамическая система.

В дальнейшем нас будут интересовать только динамические системы.

Функция системы

Свойства системы проявляются не только значениями выходных переменных, но и ее функцией, поэтому определение функций системы является одной из первых задач ее анализа или проектирования.

Понятие «функция» имеет разные определения: от общефилософских до математических.

Функция как общефилософское понятие. Общее понятие функции включает в себя понятия «предназначение» (целевое назначение) и «способность» (служить каким-то целям). Функция — внешнее проявление свойств объекта.

Примеры:

1. Ручка двери имеет функцию помочь ее открыть.

2. Налоговая служба имеет функцию сбора налогов.

3 Функция информационной системы — обеспечение информацией лица, принимающего решения.

4. Функция картины в известном мультфильме — закрывать дырку в стене.

5. Функция ветра — разгонять смог в городе.

Система может быть одно- или многофункциональной. В зависимости от степени воздействия на внешнюю среду и характера взаимодействия с другими системами, функции можно распределить по возрастающим рангам:

- пассивное существование, материал для других систем (подставка для ног);

- обслуживание системы более высокого порядка (выключатель в компьютере);

- противостояние другим системам, среде (выживание, охранная система, система защиты);

- поглощение (экспансия) других систем и среды (уничтожение вредителей растений, осушение болот);

- преобразование других систем и среды (компьютерный вирус, пенитенциарная система).

Функция в математике. Функция — это одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Формально функцию можно определить так: Элемент множества Еy произвольной природы называется функцией элемента х, определенной на множестве Еx произвольной природы, если каждому элементу х из множества Еx соответствует единственный элемент у 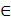Еy. Элемент х называется независимой переменной, или аргументом. Функция может задаваться: аналитическим выражением, словесным определением, таблицей, графиком и т. Д.

Функция как кибернетическое понятие. Философское определение отвечает на вопрос: «Что может делать система?». Этот вопрос правомерен как для статических, так и для динамических систем. Однако для динамических систем важен ответ на вопрос: «Как она это делает?». В этом случае, говоря о функции системы, будем иметь в виду следующее: Функция системы — это способ (правило, алгоритм) преобразование входной информации в выходную информацию.

Функцию динамической системы можно представить логико-математической моделью, связывающей входные (X) и выходные (Y) координаты системы, — моделью «вход-выход»:

Y = F(Х),

где F – оператор (в частном случае некоторая формула), называемый алгоритмом функционирования, — вся совокупность математических и логических действий, которые нужно произвести, чтобы по данным входам Х найти соответствующие выходы Y.

Удобно было бы представить оператор F в виде некоторых математических соотношений, однако это не всегда возможно.

В кибернетике широко используется понятие «черный ящик». «Черный ящик» является кибернетической моделью или моделью «вход-выход», в которой не рассматривается внутренняя структура объекта (либо о ней абсолютно ничего не известно, либо делается такое допущение). В этом случае о свойствах объекта судят только на основании анализа его входов и выходов. (Иногда употребляют термин «серый ящик», когда о внутренней структуре объекта все же что-либо известно.) Задачей системного анализа как раз и является «осветление» «ящика» — превращение черного в серый, а серого — в белый.

Условно можно считать, что функция F состоит из структуры St и параметров :

F={St,A},

что в какой-то мере отражает соответственно структуру системы (состав и взаимосвязь элементов) и ее внутренние параметры (свойства элементов и связей).

Функционирование системы

Функционирование рассматривается как процесс реализации системой своих функций. С кибернетической точки зрения:

Функционирование системы — это процесс переработки входной информации в выходную.

Математически функционирование можно записать так:

Y{t} = F(X(t)).

Функционирование описывает, как меняется состояние системы при изменении состояния ее входов.

Состояние функции системы

Функция системы является ее свойством, поэтому можно говорить о состоянии системы в заданный момент времени, указывая ее функцию, которая справедлива в этот момент времени. Таким образом, состояние системы можно рассматривать в двух разрезах: состояние ее параметров и состояние ее функции, которая, в свою очередь, зависит от состояния структуры и параметров:

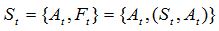
Знание состояния функции системы позволяет прогнозировать значения ее выходных переменных. Это успешно удается для стационарных систем.
Систему считают стационарной, если ее функция практически не изменяется в течение определенного периода ее существования. Для такой системы реакция на одно и то же воздействие не зависит от момента приложения этого воздействия.

Ситуация значительно осложняется, если функция системы меняется во времени, что характерно для нестационарных систем.

Систему считают нестационарной, если ее функция изменяется со временем.
Не стационарность системы проявляется различными ее реакциями на одни и те же возмущения, приложенные в разные периоды времени. Причины не стационарности системы лежат внутри нее и заключаются в изменении функции системы: структуры (St) и/или параметров (А).

Иногда стационарность системы рассматривают в узком смысле, когда обращают внимание на изменение только внутренних параметров (коэффициентов функции системы).

Стационарной называют систему, все внутренние параметры которой не изменяются во времени.

Нестационарная система — это система с переменными внутренними параметрами.

Пример. Рассмотрим зависимость прибыли от продажи некоторого товара (П) от цены на него (Ц).

Пусть сегодня эта зависимость выражается математической моделью:

П = -50+30Ц-3Ц²

Если через некоторое время изменится ситуация на рынке, то изменится и наша зависимость – она станет например такой:

П = -62 + 24Ц -4Ц²

Режимы динамической системы

Следует различать три характерных режима, в которых может находиться динамическая система: равновесный, переходной и периодический.

Равновесный режим (равновесное состояние, состояние равновесия) — это такое состояние системы, в котором она может находиться сколь угодно долго в отсутствие внешних возмущающих воздействий или при постоянных воздействиях. Однако надо понимать, что для экономических и организационных систем понятие «равновесие» применимо достаточно условно.

Пример. Простейший пример равновесия — шарик, лежащий на плоскости.

Под переходным режимом (процессом) будем понимать процесс движения динамической системы из некоторого начального состояния к какому-либо ее установившемуся режиму – равновесному или периодическому.

Периодическим режимом называется такой режим, когда система через равные промежутки времени приходит в одни и те же состояния.

Пространство состояний

Поскольку свойства системы выражаются значениями ее выходов, то состояние системы можно определить как вектор значений выходных переменных Y = (y₁,..,y_m). Выше говорилось, что среди составляющих вектора Y, кроме непосредственно выходных переменных появляются произвольные от них.

Поведение системы (ее процесс) можно изображать разными способами. Например, при m выходных переменных могут быть следующие формы изображения процесса:

- в виде таблицы значений выходных переменных для дискретных моментов времени t₁,t₂…t_k;

- в виде m графиков в координатах y_i – t, i = 1,…,m;

- в виде графика в m-мерной системе координат.

Остановимся на последнем случае. В m-мерной системе координат каждой точке соответствует определенное состояние системы.

Множество возможных состояний системы Y (у ∈ Y) рассматривают как пространство состояний (или фазовое пространство) системы, а координаты этого пространства называют фазовыми координатами.

В фазовом пространстве каждый его элемент полностью определяет состояние системы.
Точка, соответствующая текущему состоянию системы, называется фазовой, или изображающей, точкой.

Фазовая траектория — это кривая, которую описывает фазовая точка при изменении состояния невозмущенной системы (при неизменных внешних воздействиях).
Совокупность фазовых траекторий, соответствующих всевозможным начальным условиям, называется фазовым портретом.

Фазовый портрет фиксирует только направление скорости фазовой точки и, следовательно, отражает лишь качественную картину динамики.

Дата добавления: 2018-02-15; просмотров: 5740; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!