Особенности работы нормальных алгоритмов Маркова.
Нормальные алгоритмы Маркова.
В данном параграфе дается представление об еще одном подходе к уточнению понятия алгоритма, предложенном в 1947 году А.А. Марковым и называемом нормальные алгоритмы (в авторской транскрипции – алгорифмы). Данный подход связывает неформальное понятие эффективности с переработкой слов в некотором конечном алфавите в соответствии с определенными правилами. В качестве элементарного преобразования используется подстановка одного слова вместо другого. Множество таких подстановок определяет схему алгоритма. Правила, определяющие порядок применения подстановок, а также правила остановки являются общими для всех нормальных алгоритмов. Дадим формальные определения.
Определение 19:Нормальный алгоритм Маркова – это аппарат преобразования слов. Под словом подразумевается произвольная последовательность символов, входящих в конечный алфавит.
Обозначения:  – слово,
– слово, 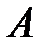 – алфавит.
– алфавит.
Алфавит символов зависит от конкретной задачи и может содержать буква, цифры, знаки препинания.
Определение 20: Каждый нормальный алгоритм Маркова представляет собой совокупность правил 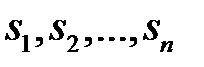 , которыеназываются правилами подстановки. Каждое правило подстановки
, которыеназываются правилами подстановки. Каждое правило подстановки 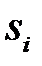 можно представить в виде преобразования:
можно представить в виде преобразования:  .
.
Преобразование произвольного слова 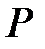 состоит в поиске в нем подслова, совпадающего с левой частью
состоит в поиске в нем подслова, совпадающего с левой частью 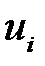 некоторого правила подстановки
некоторого правила подстановки 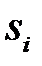 , и замене этого подслова правой частью
, и замене этого подслова правой частью 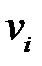 данного правила.
данного правила.
Для краткости в дальнейшем правила подстановки будем обозначать натуральными числами.
Приведем пример нормального алгоритма Маркова.
Пример 1. Алфавит символов  . Данный алгоритм содержит два правила подстановки:
. Данный алгоритм содержит два правила подстановки:
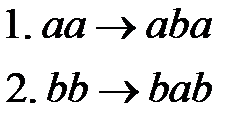
Применить этот алгоритм к слову 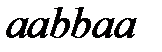 .
.
Решение.
Применяя данный алгоритм к данному слову, будут произведены следующие замены (преобразования):
1) 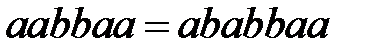 по правилу (1),
по правилу (1),
2) 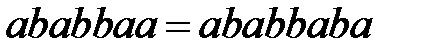 по правилу (1),
по правилу (1),
3) 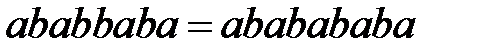 по правилу (2).
по правилу (2).
Ответ: на выходе получается слово 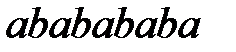 .
.
Дадим четкое описание алгоритма преобразования произвольного слова.
Согласно концепции нормальных алгоритмов Маркова, преобразование слова 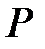 по правилам подстановки
по правилам подстановки 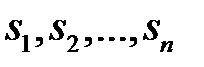 представляет собой последовательность однотипных шагов. Опишем один шаг преобразования.
представляет собой последовательность однотипных шагов. Опишем один шаг преобразования.
1) Последовательно просматриваются правила 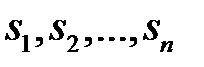 .
.
2) Если левая часть 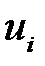 некоторого правила подстановки
некоторого правила подстановки 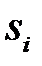 входит в слово, то вхождение
входит в слово, то вхождение 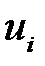 меняется на
меняется на 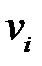 .
.
Эти шаги преобразования последовательно выполняются один за другим. Возникает вопрос: когда следует завершать преобразование слова? Согласно концепции нормальных алгоритмов Маркова, завершение преобразование слова происходит в двух случаях:
1) На некотором шаге преобразования ни одно из правил 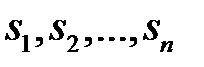 оказывается неприменимым к данному слову, т.е. ни одна из левых частей
оказывается неприменимым к данному слову, т.е. ни одна из левых частей 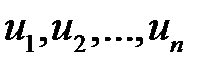 не содержится в слове.
не содержится в слове.
2) Существует два вида правил подстановки: терминальные и нетерминальные. Если на некотором шаге преобразования к слову было применено терминальное правило, то процесс преобразования считается завершенным, т.е. новый просмотр не производится.
В терминальных правилах вместо символа  используется символ
используется символ  .
.
Замечание 1. Если левая часть некоторого правила входит в слово более одного раза, то заменяется только самое левое вхождение в слово (на одном шаге преобразования).
Замечание 2. После каждого применения к слову некоторого правила 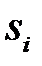 новый просмотр правил всегда начинается с правила
новый просмотр правил всегда начинается с правила 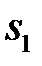 .
.
Замечание 3. Левая часть правила может быть пустой. Правило с пустой левой частью считается применимым к любому слову. Его действие состоит в том, что к началу слова добавляется правая часть правила.
Замечание 4. Правая часть правила тоже может быть пустой. Результатом применения такого правила является удаление из слова последовательности символов, совпадающих с левой частью данного правила.
Если вернуться к примеру 1, можно понять, что правило 1 применяется до тех пор, пока его можно применять. Правило 2 начинает применяться к слову только после того как правило 1 становится к нему неприменимым. После третьего шага оба правила неприменимы.
Пример 2. Алфавит символов  . Данный алгоритм содержит два правила подстановки:
. Данный алгоритм содержит два правила подстановки:
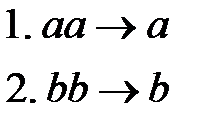
Применить этот алгоритм к словам 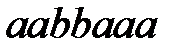 ,
, 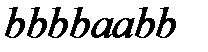 .
.
Решение.
1)  .
.
2) 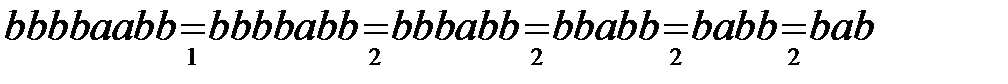 .
.
Этот алгоритм из нескольких одинаковых подряд стоящих букв оставляет только одну букву.
Пример 3. Алфавит символов  . Данный алгоритм содержит два правила подстановки:
. Данный алгоритм содержит два правила подстановки:
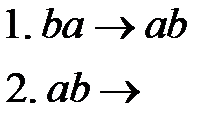
Применить этот алгоритм к слову 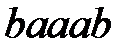 .
.
Решение.
Заметим, что правая часть второго правила пустая.
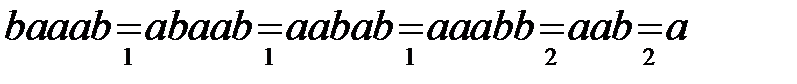 .
.
На двух последних шагах происходит удаление пары 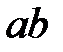 . Итоговое слово
. Итоговое слово 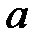 . Ни одно из правил подстановки к нему не применимо.
. Ни одно из правил подстановки к нему не применимо.
Вывод: Данный нормальный алгоритм Маркова сначала переставляет в слове буквы 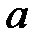 и
и 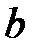 так, чтобы все буквы
так, чтобы все буквы 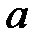 стояли раньше, чем
стояли раньше, чем 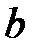 . Правило 1 применяется до тех пор, пока хотя бы одна буква
. Правило 1 применяется до тех пор, пока хотя бы одна буква 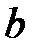 стоит перед
стоит перед 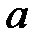 . После того, как пар
. После того, как пар 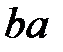 не останется, удаляются пары
не останется, удаляются пары 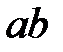 . На выходе в слове останутся те буквы, которых в исходном слове было больше. При одинаковом количестве букв результатом будет пустая строка.
. На выходе в слове останутся те буквы, которых в исходном слове было больше. При одинаковом количестве букв результатом будет пустая строка.
Пример 4. Алфавит символов  . Данный алгоритм содержит два правила подстановки:
. Данный алгоритм содержит два правила подстановки:
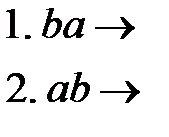
Применить этот алгоритм к слову 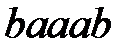 .
.
Решение.
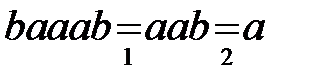 .
.
Данный алгоритм Маркова эквивалентен алгоритму, рассмотренному в предыдущем примере. Оба алгоритма дают один и тот же результат, происходит удаление пар символов. Однако, это алгоритм работает быстрее предыдущего. Для преобразования одного и того же слова потребовалось всего два шага вместо пяти. Значит, данный способ преобразования более эффективный.
Особенности работы нормальных алгоритмов Маркова.
1) Перестановка местами правил подстановки может влиять как на последовательность преобразований, так и на конечный результат.
Чтобы этот факт проиллюстрировать, рассмотрим пример 3, но правила подстановки поменяем местами.
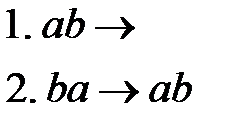
Преобразуем то же слово:  .
.
Видно, что меняется последовательность преобразований, но результат остается прежним.
Пример 5. Алфавит символов  . Данный алгоритм содержит два правила подстановки:
. Данный алгоритм содержит два правила подстановки:
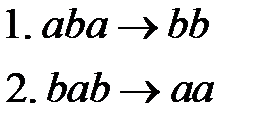
Применить этот алгоритм к словам 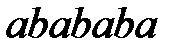 .
.
Решение.
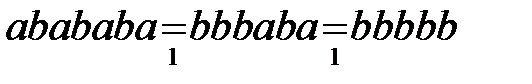 .
.
Изменим порядок следования правил подстановки и применим алгоритм к тому же слову:
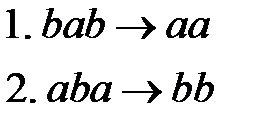
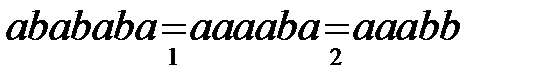 .
.
Видно, что меняется как результат, так и последовательность преобразований.
2) Правило подстановки с пустой левой частью применимо к любому слову. Это означает, что оно должно всегда быть последним в списке правил. Иначе оно блокирует все последующие правила.
Пример 6. Алфавит символов  . Данный алгоритм содержит три правила подстановки:
. Данный алгоритм содержит три правила подстановки:

Применить этот алгоритм к словам 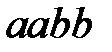 .
.
Решение.
 и т.д.
и т.д.
Третье правило заблокировано, оно недостижимо и никогда не выполнится.
3) Если в списке правил подстановки есть правило с пустой левой частью, то для завершения работы алгоритма Маркова в нем должно присутствовать хотя бы одно терминальное правило подстановки.
В самом деле, условие окончания преобразования слова – либо нет подходящего правила подстановки, либо применено терминальное правило. Так как правило с пустой левой частью применимо к любому слову, то единственным условием окончания преобразования является применение к нему терминального правила подстановки.
Пример 7. Алфавит символов  . В данном случае среди правил нет терминального правила подстановки, следовательно, процесс преобразования любого слова будет бесконечным.
. В данном случае среди правил нет терминального правила подстановки, следовательно, процесс преобразования любого слова будет бесконечным.
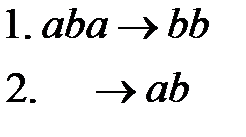
Второе правило всегда применимо и добавляет к началу слова буквы 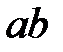 . Применим этот алгоритм к словам
. Применим этот алгоритм к словам  :
:
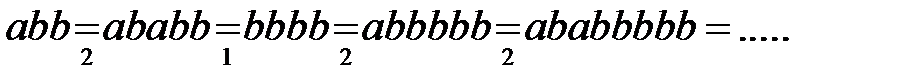
Если в первое правило будет терминальным, тогда процесс преобразования слова завершится сразу после его применения, в нашем случае на втором шаге:
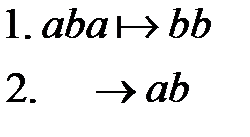
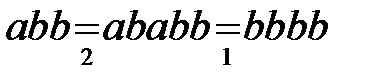 .
.
Возможны случаи, когда, не смотря на наличие терминального правила подстановки, процесс преобразования слова является бесконечным. Такие примеры будут приведены ниже.
4) Пусть имеется два правила подстановки 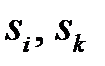 , такие, что левая часть одного правила
, такие, что левая часть одного правила  является подстрокой левой части
является подстрокой левой части 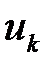 другого правила. Тогда правило
другого правила. Тогда правило 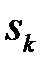 (более длинное слово) должно стоять в списке правил выше правила
(более длинное слово) должно стоять в списке правил выше правила 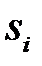 (короткое слово). В противном случае правило
(короткое слово). В противном случае правило 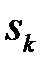 никогда не выполнится.
никогда не выполнится.
Пример 8. Алфавит символов  . Рассмотрим следующие правила подстановки:
. Рассмотрим следующие правила подстановки:
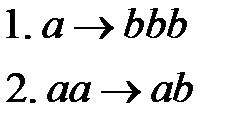
Видно, что левая часть первого правила 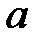 - это подстрока левой части
- это подстрока левой части 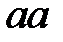 второго правила. Второе правило подстановки никогда не будет применено ни к какому слову. В самом деле, если в некоторое слово входит
второго правила. Второе правило подстановки никогда не будет применено ни к какому слову. В самом деле, если в некоторое слово входит 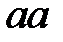 , то входит и одна буква
, то входит и одна буква 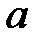 . Следовательно, к такому слову всегда будет применяться только первое правило подстановки. Можно сказать, что первое правило блокирует выполнение второго правила.
. Следовательно, к такому слову всегда будет применяться только первое правило подстановки. Можно сказать, что первое правило блокирует выполнение второго правила.
Рассмотрим применение этого алгоритма к слову 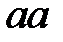 :
:
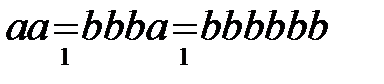 .
.
Поменяем правила местами:
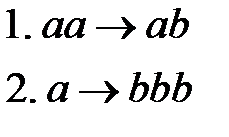
Тогда в процессе преобразования слова может быть применено как первое, так и второе правила подстановки:
 .
.
Задачи.
Рассмотрим примеры на составление нормальных алгоритмов Маркова.
Задача 1. Алфавит символов 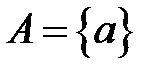 . Составить нормальный алгоритм Маркова, удваивающий в слове каждую букву
. Составить нормальный алгоритм Маркова, удваивающий в слове каждую букву 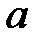 .
.
Решение.
Можно рассмотреть алгоритм Маркова, состоящий из одного правила подстановки:
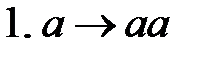 .
.
Сразу отметим, что этот алгоритм задачу удвоения не решает, так как он просто добавляет по одной букве 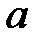 к слову на каждом шаге преобразования. Например, на входе слово
к слову на каждом шаге преобразования. Например, на входе слово 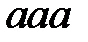 :
:
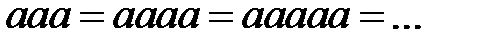 .
.
Удваивания символа не происходит. Значит, приведенный алгоритм не верный.
Для решения подобных задач составляется нормальный алгоритм Маркова, который выполняет следующие преобразования слова:
1) К началу слова добавляется дополнительный символ  . Этот символ не входит в алфавит.
. Этот символ не входит в алфавит.
2) Дополнительный символ "прогоняется" через слово с одновременной заменой каждого символа в слове согласно условию задачи.
3) В конце преобразований дополнительный символ удаляется.
Данные действия для нашей задачи удвоения символов будут реализованы следующим нормальным алгоритмом Маркова:
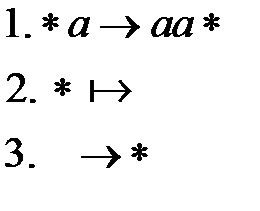
Имеется три правила подстановки. Третье правило добавляет к слову дополнительный символ  . Это правило состоит из пустой левой части, его можно применить всегда к любому слову. С помощью первого правила подстановки символ
. Это правило состоит из пустой левой части, его можно применить всегда к любому слову. С помощью первого правила подстановки символ  "прогоняется" через слово с одновременной заменой
"прогоняется" через слово с одновременной заменой 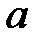 на
на 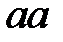 . В результате этого символ
. В результате этого символ  оказывается в конце слова. Второе правило удаляет символ
оказывается в конце слова. Второе правило удаляет символ  по окончании преобразования слова. Это правило является терминальным, поэтому его применение означает завершение преобразования слова. Новый просмотр правил не производится.
по окончании преобразования слова. Это правило является терминальным, поэтому его применение означает завершение преобразования слова. Новый просмотр правил не производится.
Посмотрим, как данный нормальный алгоритм Маркова преобразует входное слово 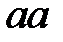 и
и 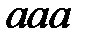 :
:
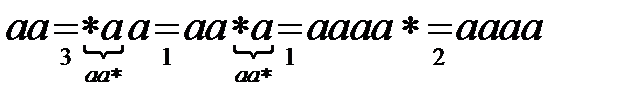 ;
;
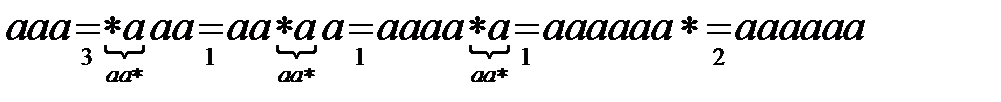 .
.
По опыту предыдущей задачи можно сделать следующие важные замечания.
Замечание 1. Правило с пустой левой частью всегда должно стоять в списке правил на последнем месте. Применяться же оно должно раньше остальных правил. То есть никакое другое правило не должно быть применено к слову до применения к нему последнего правила. А это в свою очередь означает, что все правила (кроме последнего) должны содержать в своей левой части дополнительный символ  .
.
Согласно концепции нормальных алгоритмов Маркова, дополнительные символы (символы, не входящие в алфавит) не могут содержаться в исходном слове. Они могут входить в слово в процессе его преобразования. Поэтому, любое правило, содержащее в своей левой части дополнительный символ, к исходному слову не применимо.
Замечание 2. Правило, удаляющее дополнительный символ, должно быть применено лишь после того, как будет завершен процесс преобразования слова согласно условию задачи, т.е. после "прохода" символа  через слово.
через слово.
В нашем примере это происходит только тогда, когда становится неприменимым первое правило.
Замечание 3. Правило, удаляющее дополнительный символ, должно быть терминальным. Иначе процесс преобразования слова станет бесконечным.
Задача 2. Алфавит символов  . Составить нормальный алгоритм Маркова, который выполняет инверсию (букву
. Составить нормальный алгоритм Маркова, который выполняет инверсию (букву 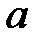 меняет на
меняет на 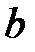 и наоборот).
и наоборот).
Решение.
Сразу заметим, что алгоритм Маркова, состоящий из двух правил:
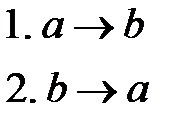 ,
,
задачу не решает.
Эта задача не решается и с помощью алгоритма Маркова, состоящего из трех правил (обмен значений двух переменных с использованием дополнительной третьей переменной):
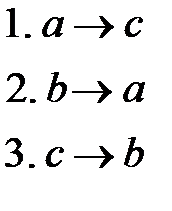
В случае алгоритмов Маркова этот метод не работает.
Для решения этой задачи необходимо действовать так же, как в предыдущей задаче (по пунктам 1-3 плана). Все эти действия реализуют нормальный алгоритм Маркова:
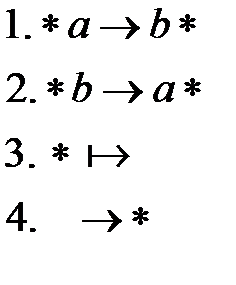
Посмотрим, как данный нормальный алгоритм Маркова преобразует входное слово 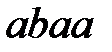 :
:
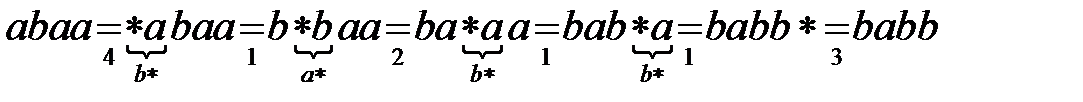 .
.
Задача 3. Алфавит символов  . Составить нормальный алгоритм Маркова, который удваивает последнюю букву в слове.
. Составить нормальный алгоритм Маркова, который удваивает последнюю букву в слове.
Решение.
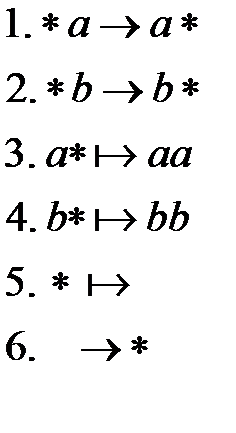
Идея построения алгоритма аналогична рассмотренному в предыдущих примерах. Сначала вводим дополнительный символ  (правило 6). "Прогоняем" его через слово без изменения слова (правила 1 и 2). После этого (справа от
(правило 6). "Прогоняем" его через слово без изменения слова (правила 1 и 2). После этого (справа от  не осталось символов) удваиваем символ слева от
не осталось символов) удваиваем символ слева от  (терминальные правила 3 и 4). Удаляем вспомогательный символ. Правило 5 необходимо для корректной обработки пустого слова. Согласно концепции нормальных алгоритмов Маркова, исходное слово может быть пустым, т.е. не содержать ни одного символа. В данном случае пустое слово нужно оставить без изменения.
(терминальные правила 3 и 4). Удаляем вспомогательный символ. Правило 5 необходимо для корректной обработки пустого слова. Согласно концепции нормальных алгоритмов Маркова, исходное слово может быть пустым, т.е. не содержать ни одного символа. В данном случае пустое слово нужно оставить без изменения.
Посмотрим, как данный нормальный алгоритм Маркова преобразует входные слова  ,
, 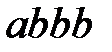 и пустое слово:
и пустое слово:
 ;
;
 ;
;
пустое слово: 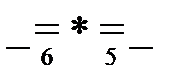
Задача 4. Алфавит символов  . Удвоить в слове все буквы, кроме последней.
. Удвоить в слове все буквы, кроме последней.
Решение.
Идея алгоритма состоит в том, что символ  "прогоняется" через слово с одновременным удваиванием в нем каждой буквы (правила 1 и 2). После этого
"прогоняется" через слово с одновременным удваиванием в нем каждой буквы (правила 1 и 2). После этого  удаляется вместе с последним символом строки (терминальные правила 3 и 4). Правило 5 необходимо для корректной обработки пустого слова. Эти этапы реализуются следующим нормальным алгоритмом Маркова:
удаляется вместе с последним символом строки (терминальные правила 3 и 4). Правило 5 необходимо для корректной обработки пустого слова. Эти этапы реализуются следующим нормальным алгоритмом Маркова:
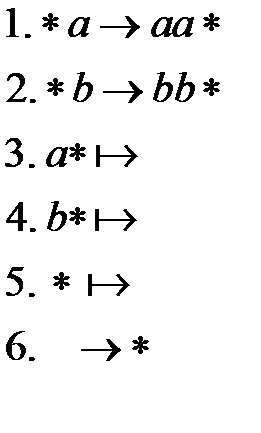
Исходное слово 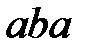 :
:
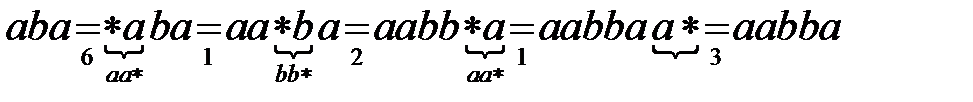 .
.
Задача 5. Алфавит символов 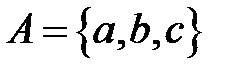 . Составить нормальный алгоритм Маркова, который удаляет из слова первую букву.
. Составить нормальный алгоритм Маркова, который удаляет из слова первую букву.
Решение.
В данном случае символ  не надо "прогонять" через слово. Он будет удален с первой буквой слова. Задачу решает алгоритм Маркова, содержащий пять правил подстановки:
не надо "прогонять" через слово. Он будет удален с первой буквой слова. Задачу решает алгоритм Маркова, содержащий пять правил подстановки:

Исходное слово 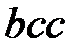 :
: 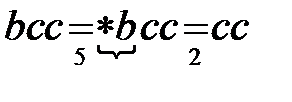 .
.
Исходное слово 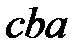 :
: 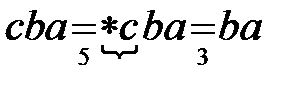 .
.
Задача 6. Алфавит символов  . Составить нормальный алгоритм Маркова, который оставляет в слове только первую букву.
. Составить нормальный алгоритм Маркова, который оставляет в слове только первую букву.
Решение.
Идея алгоритма состоит в том, чтобы удалить из слова вторую, третью и последующие буквы (правила 1-4). Эти правила удаляют второй символ после символа  . При этом, символ
. При этом, символ  находится слева от слова. Как только все буквы, кроме первой, будут удалены, преобразование слова завершается. Пятое терминальное правило удаляет вспомогательный символ.
находится слева от слова. Как только все буквы, кроме первой, будут удалены, преобразование слова завершается. Пятое терминальное правило удаляет вспомогательный символ.

Преобразуем с помощью алгоритма слова  и
и 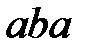 :
:
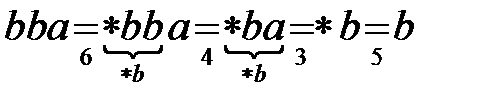 ;
;
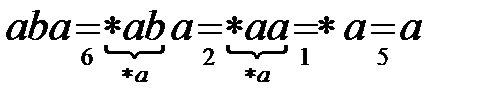 .
.
Для нормальных алгоритмов разработана техника программирования, позволяющая осуществлять операции композиции алгоритмов, реализовывать операторы «если Ф, то выполнить F1, иначе F2», «пока Ф, выполнять F1, иначе F2». Следовательно, класс функций достаточно широк.
Теорема. Класс функций М, вычислимых по Маркову, совпадает с классом функций Т, вычислимых по Тьюрингу, и, следовательно, с классом частично рекурсивных функций Ч и с классом вычислимых функций Е.
Дата добавления: 2018-02-15; просмотров: 9816; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
