Применимость нормальных алгоритмов Маркова к словам.
Определение 21. Нормальный алгоритм Маркова называется применимым к некоторому слову, если последовательность шагов преобразования этого слова является конечной. В противном случае (последовательность шагов преобразования слова бесконечная) нормальный алгоритм Маркова называется неприменимым к слову, т.е. алгоритм зацикливается на этом слове.
Замечание. Не стоит путать неприменимость правила подстановки к слову на шаге преобразования и неприменимость всего алгоритма Маркова.
Пример 1. Алфавит символов  . Данный алгоритм содержит два правила подстановки:
. Данный алгоритм содержит два правила подстановки:

Данный нормальный алгоритм Маркова применим к слову, содержащему хотя бы одну букву  , или к пустому слову. При этом он добавляет к непустому слову букву
, или к пустому слову. При этом он добавляет к непустому слову букву  , после чего останавливается. К словам, содержащим только буквы
, после чего останавливается. К словам, содержащим только буквы  , этот алгоритм неприменим.
, этот алгоритм неприменим.
Пример 2. Алфавит символов  . Данный алгоритм содержит два правила подстановки:
. Данный алгоритм содержит два правила подстановки:
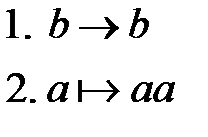
Поменяли местами правила подстановки. Полученный нормальный алгоритм Маркова применим к любому слову, не содержащему букв  , в том числе, к пустому слову. Он неприменим к любому слову, содержащему хотя бы одну букву
, в том числе, к пустому слову. Он неприменим к любому слову, содержащему хотя бы одну букву  .
.
Пример 3. Алгоритм содержит одно правило подстановки:  . Левая и правая части этого правила пустые. Данный алгоритм Маркова неприменим ни к одному слову, так как данное правило подстановки будет применено к любому слову бесконечное число раз.
. Левая и правая части этого правила пустые. Данный алгоритм Маркова неприменим ни к одному слову, так как данное правило подстановки будет применено к любому слову бесконечное число раз.
Пример 4. Алгоритм содержит одно правило подстановки:  . Это правило является терминальным с пустой левой и правой частями. Этот нормальный алгоритм применим к любому слову, так как после однократного применения правила подстановки работа алгоритма завершается.
. Это правило является терминальным с пустой левой и правой частями. Этот нормальный алгоритм применим к любому слову, так как после однократного применения правила подстановки работа алгоритма завершается.
|
|
|
Определение 22. Два нормальных алгоритма Маркова называются эквивалентными, если их области применимости совпадают и для любого слова из области применимости они выдают один и тот же результат.
Пример 5. Алфавит символов  . Данный алгоритм содержит два правила подстановки:
. Данный алгоритм содержит два правила подстановки:

Данный алгоритм применим к любому слову, не содержащему букв  . Он будет неприменим к слову, содержащему хотя бы одну букву
. Он будет неприменим к слову, содержащему хотя бы одну букву  . Рассмотрим преобразование слов
. Рассмотрим преобразование слов  и
и 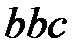 :
:
 (остановка);
(остановка);
 (зацикливание).
(зацикливание).
Пример 6. Алфавит символов  . Данный алгоритм содержит два правила подстановки:
. Данный алгоритм содержит два правила подстановки:

Данный алгоритм Маркова эквивалентен алгоритму из предыдущей задачи. Области применимости этих двух алгоритмов совпадают (слова, не содержащие букв  ). Слова, взятые из области применимости, преобразуются этими алгоритмами одинаково.
). Слова, взятые из области применимости, преобразуются этими алгоритмами одинаково.
 (остановка);
(остановка);
 (зацикливание).
(зацикливание).
Не важно, что зацикливание происходит по-разному, важен только результат на области применимости. Этого достаточно для эквивалентности алгоритмов.
|
|
|
Задачи.
Рассмотрим примеры на применимость нормальных алгоритмов Маркова.
Задача 1. Алфавит символов 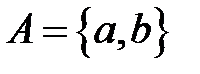 . Составить алгоритм Маркова, применимый к словам четной длины (к словам нечетной длины он неприменим соответственно).
. Составить алгоритм Маркова, применимый к словам четной длины (к словам нечетной длины он неприменим соответственно).
Решение.
Данную задачу решает нормальный алгоритм Маркова, состоящий из трех правил подстановки:

Для данной задачи имеет значение лишь количество букв в слове, поэтому меняем все буквы  на
на  (правило 1). Кроме того, имеет значение четность числа букв в слове, значит, удаляем все пары
(правило 1). Кроме того, имеет значение четность числа букв в слове, значит, удаляем все пары 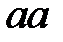 (правило 2). При этом четность не меняется. В результате первых двух преобразований остается либо пустое слово, если исходное слово имело четную длину, либо слово
(правило 2). При этом четность не меняется. В результате первых двух преобразований остается либо пустое слово, если исходное слово имело четную длину, либо слово  , если оно имело нечетную длину. Зацикливаем алгоритм на слове
, если оно имело нечетную длину. Зацикливаем алгоритм на слове  (правило 3). К пустому же слову ни одно из правил подстановки не применимо. Значит, алгоритм Маркова завершается (алгоритм применим).
(правило 3). К пустому же слову ни одно из правил подстановки не применимо. Значит, алгоритм Маркова завершается (алгоритм применим).
Применим рассмотренный алгоритм к словам  и
и  :
:
 (зацикливание);
(зацикливание);
 (остановка).
(остановка).
Задача 2. Алфавит символов 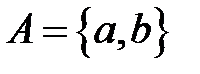 . Составить алгоритм Маркова, применимый к словам нечетной длины.
. Составить алгоритм Маркова, применимый к словам нечетной длины.
Решение.
Данную задачу решает нормальный алгоритм Маркова, состоящий из четырех правил подстановки:
|
|
|

В отличие от предыдущей задачи, нужно остановить работу алгоритма Маркова на любом слове нечетной длины и зациклить на любом слове четной длины. Поэтому первые два правила преобразование те же. В результате останется либо пустое слово, либо слово  . Остановка на этом слове происходит с помощью третьего правила. Зацикливание на пустом слове происходит при исполнении последнего правила.
. Остановка на этом слове происходит с помощью третьего правила. Зацикливание на пустом слове происходит при исполнении последнего правила.
Применим рассмотренный алгоритм к словам  и
и  :
:
 (остановка);
(остановка);
 (зацикливание).
(зацикливание).
Опишем наиболее часто используемый прием составления нормальных алгоритмов Маркова при решении задач на применимость:
1) Упрощаем исходное слово, не нарушая условия задачи.
2) Отдельно разбираем каждый случай, получившийся после упрощения.
Эти правила могут уточняться при решении конкретных задач.
Замечание. Если последнее правило по условию задачи должно быть терминальным, т.е. работа алгоритма завершается после его применения, то это правило можно не писать.
Это вытекает из того, что применение к слову на некотором шаге преобразования последнего правила подстановки означает неприменимость к нему всех остальных правил подстановки. Работа алгоритма все равно завершится.
|
|
|
Заметим, что данное утверждение справедливо только для задач на применимость, когда важен лишь факт остановки или зацикливания, а результирующее слово не имеет значения.
Задача 3. Алфавит символов 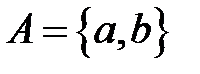 . Составить алгоритм Маркова, применимый к любому непустому слову четной длины.
. Составить алгоритм Маркова, применимый к любому непустому слову четной длины.
Решение.
Данную задачу решает нормальный алгоритм Маркова, состоящий из четырех правил подстановки:

Сначала происходит упрощение исходного слова (правило 1). Просто удалять пары  нельзя, так как в этом случае слово
нельзя, так как в этом случае слово  будет преобразовано в пустое слово, что нарушает условие задачи. Поэтому, удаляем пары
будет преобразовано в пустое слово, что нарушает условие задачи. Поэтому, удаляем пары  , но так, чтобы оставалась хотя бы одна буква
, но так, чтобы оставалась хотя бы одна буква  (правило 2). В результате применения первых двух правил остается либо слово
(правило 2). В результате применения первых двух правил остается либо слово  , либо слово
, либо слово  , либо пустое слово. Останавливаемся на слове
, либо пустое слово. Останавливаемся на слове  (правило 3), зацикливаем алгоритм на слове
(правило 3), зацикливаем алгоритм на слове  , либо на пустом слове (правило 4).
, либо на пустом слове (правило 4).
Применим рассмотренный алгоритм к словам  и
и  :
:
 (зацикливание);
(зацикливание);
 (остановка).
(остановка).
Для преобразования пустого слова:
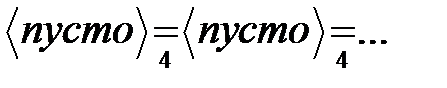 (зацикливание).
(зацикливание).
Утверждение. Если некоторое правило подстановки применимо к некоторому слову  , то оно применимо и к слову
, то оно применимо и к слову  , в которое слово
, в которое слово  входит как подслово.
входит как подслово.
Например, если правило подстановки применимо к слову  , тогда его левая часть либо
, тогда его левая часть либо  , либо
, либо  , либо пустое слово. Значит, данное правило применимо, например, к словам
, либо пустое слово. Значит, данное правило применимо, например, к словам  ,
,  ,
,  ,
,  , …
, …
Вывод: Если необходимо выполнить одинаковые действия (остановить или зациклить алгоритм), как для слова  , так и для слова
, так и для слова  , то достаточно написать только одно правило подстановки с левой частью, представляющей собой слово
, то достаточно написать только одно правило подстановки с левой частью, представляющей собой слово  (более короткое слово).
(более короткое слово).
Задача 4. Алфавит символов  . Составить нормальный алгоритм Маркова, применимый к словам длины 2, 8, 14 и т.д.
. Составить нормальный алгоритм Маркова, применимый к словам длины 2, 8, 14 и т.д.
Решение.
Данную задачу решает нормальный алгоритм Маркова, состоящий из четырех правил подстановки:

Дата добавления: 2018-02-15; просмотров: 4001; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
