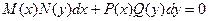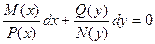Однородные ДУ первого порядка
Тема. Дифференциальные уравнения
Понятие дифференциального уравнения
Дифференциальным уравнением (ДУ) называется ____________________________________
____________________________________________________________________________________________________________________________________________________________________
Порядок ДУ задаётся______________________________________________________________
______________________________________________________________________
 |
Тогда, ДУ первого порядка в общем виде можно представить, как:
 |
ДУ второго порядка в общем виде можно представить, как:
Для того чтобы решить ДУ 1-го порядка его нужно ______________________________________
Общим решением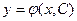 
ДУ 1-го порядка называется_______________________________
______________________________________________________________________
Частным решением 
ДУ 1-го порядка называется________________________________
______________________________________________________________________
Общим интегралом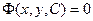 
ДУ 1-го порядка называется_____________________________
______________________________________________________________________
Частным интегралом 
ДУ1-го порядка называется____________________________
______________________________________________________________________
Геометрическое изображение решения дифференциального уравнения первого порядка. Задача Коши
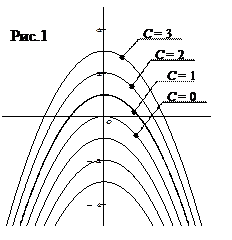Пусть - какое-нибудь решение некоторого ДУ первого порядка. Равенство можно считать уравнением, задающим график функции или линией. Эту линию называют интегральной кривой ДУ. Поскольку общее решение 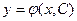ДУ является множеством бесконечного числа его частных решений, то геометрически оно представляет семейство интегральных кривых. Одна кривая этого семейства отличается от другой численным значением одного параметра – постоянной С. Поэтому общее решение (или общий интеграл) ДУ 1–го порядка геометрически представляет собой семейство интегральных кривых.
|
|
|
Пример 2.1. Рассмотрим дифференциальное уравнение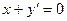 
. Его можно представить в виде 
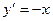. Тогда искомая неизвестная функция будет равна: 
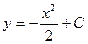. Мы получили семейство парабол, показанных на рис.1.
Каждая из этих парабол будет являться частным решением ДУ 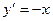при фиксированном значении С.
Пример 2.2. Найти частное решение дифференциального уравнения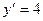 
при С = 2 и построить соответствующую интегральную кривую. (Самостоятельно)
Задача Коши
Начальным условием называется___________________________________________________
______________________________________________________________________
Начальное условие записывают в виде 
или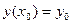 
.
Задачей Коши называется__________________________________________________________
______________________________________________________________________
Задача Коши отличается от решения примеров 2.1 и 2.2 тем, что мы, сначала, должны найти неизвестную C по некоторым начальным условиям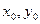 
. Геометрически это означает, что мы должны найти ту единственную кривую, которая проходит через точку 
.
|
|
|
Пример 2.3. Решить задачу Кош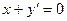и при 
.
Решение. Воспользуемся полученным ранее результатом (пример 2.1) и запишем общее решение ДУ: 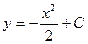. Подставляем в это равенство заданные начальные условия 
, 
:
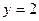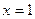. Используя найденное значение, записываем частное решение ДУ:
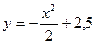. Задача Коши решена. Геометрически это решение представляет собой параболу, вершина которой имеет ординату 2,5 (см. рис.1).
Пример 2.4. Решить задачу Кош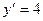и при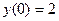 
. (Самостоятельно)
§ 3. ДУ первого порядка с разделяющимися переменными
Общий вид ДУ первого порядка с разделяющимися переменными
|
Чтобы решить такое уравнение нужно_________________________________________________
______________________________________________________________________
|
______________________________________________________________________
Пример 3.1. Решить ДУ: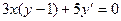 
.
Решение. Представим производную через отношение дифференциалов: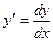 
. Тогда:
.
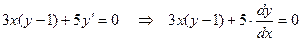Домножим левую и правую части полученного равенства на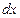 
:
.
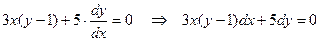Теперь разделим обе части на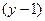 
:
.
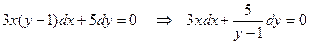Проинтегрируем результат и получим общее решение ДУ:
.
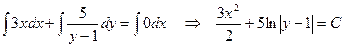Внимание! При решении данного уравнения мы «сбросили»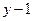 
в знаменатель, то есть ввели дополнительное условие 
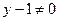. Но легко убедиться, что 
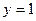тоже является корнем уравнения, так как подстановка этого значения обращает исходное ДУ в тождество: 
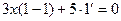. Следовательно, найденное решение ДУ необходимо дополнить и «выброшенным» частным случаем:
|
|
|
Ответ: решениями заданного ДУ являются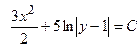 
и .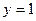
Пример 3.2. Решить ДУ: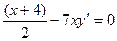 
. (Самостоятельно)
§ 4. Линейные ДУ первого порядка
Общий вид линейного ДУ первого порядка
|
где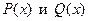 
__________________________________________________________________
Чтобы решить такое уравнение можно _________________________________________________
______________________________________________________________________
Пример 4.1. Решить ДУ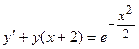 
.
Решение. Воспользуемся заменой Бернулли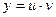 
. По правилу дифференцирования производной произведения, получим: 
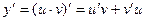. Подставляем y и 
в заданное уравнение:
.
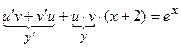Раскроем скобки и перегруппируем слагаемые следующим образом: первое оставляем в покое, а из второго и третьего вынесем одинаковый сомножитель.
.
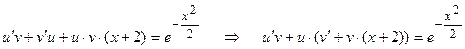Учитывая, что u и v – произвольные функции, их всегда можно подобрать так, чтобы выражение в скобках было равно «0»: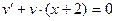 
. Решим это уравнение с разделяющимися переменными, приняв С = 0 !
.
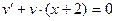
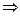
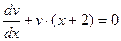
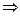
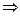
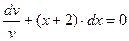
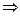
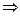
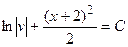
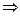
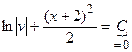
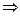
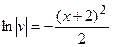Выразим из полученного равенства v, для этого проведём операцию потенцирования*:
|
|
|
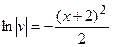
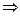
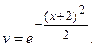
Неизвестную функцию v нашли. Найдём, теперь, функцию u. Для этого подставим найденную v в уравнение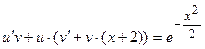 
:
.
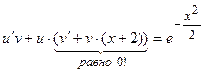
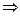
Разделяем переменные: 
.
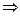
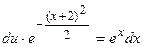
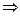
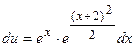Преобразуем степень экспоненты:
.
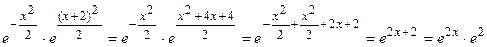*) Потенцирование - действие, заключающееся в нахождении числа по данному логарифму.
Тогда: 
.
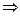
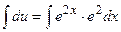
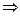
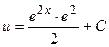Окончательно получаем общее решение заданного ДУ:
.
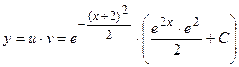Пример 4.2. Решить ДУ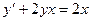 
. (Самостоятельно)
Однородные ДУ первого порядка
Определение 1. Функция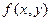 
называется однородной функцией ______________________________
_________________________________________________________________________________________
 |
Пример 5.1.
1. 
________________________________________________________________
2. 
___________________________________________________________________
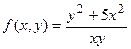Определение 2. Дифференциальное уравнение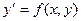 
называется однородным ДУ первого порядка, если ____________________________________________________________________________
_________________________________________________________________________________________
 |
Пример 5.2.
1. 
________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________
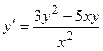2. 
_______________________________________________________________
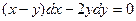Дата добавления: 2021-06-02; просмотров: 63; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!