А). Пусть последовательность задана формулой

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

у_n = 3n – 2.

Подставляя в формулу вместо n натуральные числа, находим члены последовательности:

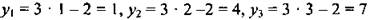и т. д.

Имеем последовательность: 1, 4, 7, ... .

Б). Пусть последовательность задана формулой

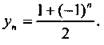
Подставляя в формулу вместо n натуральные числа, находим члены последовательности:

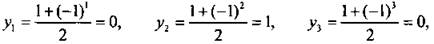
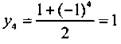и т. д.

Имеем последовательность: 0, 1, 0, 1,... .

в). Последовательность чётных чисел: y = 2n.

г).. Последовательность квадрата натуральных чисел:

y = n²: 1, 4, 9, 16, 25, ..., n², ... .

д). Стационарная последовательность: y = C; C, C, C, ...,C, ...

Частный случай: y = 5; 5, 5, 5, ..., 5, ... .

е). Последовательность y = 2ⁿ: 2, 2², 2³, 2⁴, ..., 2ⁿ, ... .

Пример последовательности, заданной аналитически

И график заданной последовательности

Построим график последовательности, заданной аналитически формулой .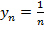

График любой последовательности – это множество всех пар значений ( n ; 1/ n ) , где n принадлежит множеству натуральных чисел.

Построим график функции 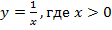(Рис. 1).

Линия графика данной функции – гипербола, и на этой ветви лежат все точки графика нашей последовательности, если n =1, то и 1/ n =1.

Из формулы получим координаты точек функции:

первая точка (1; 1); вторая точка (2; 1/2);…; и т. д.

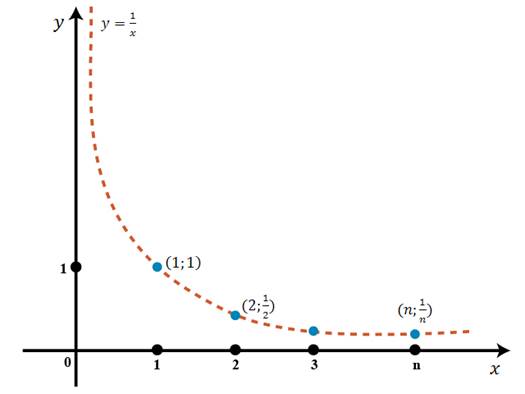Рис. 1

Так как функция y = 1/ x при х≥1 – является убывающей, следовательно, и последовательность, заданная формулой y =1/ n , также является убывающей.

2. Рекуррентный способ

Указывается правило (формула), позволяющее вычислить следующие члены последовательности , если известны её предыдущие элементы.

Пример :

А). Пусть последовательность задана формулой

у_n₊₁= 2у_n + 3 , где у₁ = 5 и n ≥ 1.

- Запишем рекуррентную формулу для n = 1:

y _n ₊₁ = 2у₁ + 3, то есть, у₂ = 2 ˟ 5 + 3 = 13.

- Запишем рекуррентную формулу для n = 2:

у₂₊₁ = 2у₂ + 3, то есть, у₃ = 2 ˟ 13 + 3 = 29.

- Запишем рекуррентную формулу для n = 3:

y ₃₊₁ = 2у₃ + 3, то есть y ₄ = 2 ˟ 29 + 3 = 61 и т. д.

Имеем последовательность: 5, 13, 29, 61, ... .

Б). Пусть последовательность задана формулой

у_n₊₂ = 2у_n₊₁ + 3у_n , где у₁ = 1, у₂ = 2 и n ≥ 1.

- Запишем рекуррентную формулу для n = 1:

у₁₊₂ = 2у₁₊₁ + 3у_1, то есть у₃ = 2у₂ + 3у_1, то есть у₃ = 2 ˟ 2 + 3 ˟ 1 = 7.

- Запишем рекуррентную формулу дляn = 2:

у₂₊₂ = 2у₂₊₁+ 3у₂ или у₄ = 2у₃ + 3у₂ = 2 ˟ 7 + 3 ˟ 2 = 20.

- Запишем рекуррентную формулу для n = 3:

у₃₊₂ = 2 y ₃₊₁ + 3 y ₃ , то есть у₅ = 2у₄ + 3у_3, то есть у₅ = 2 ˟ 20 + 3 ˟ 7 = 61 и т.д.

Имеем последовательность: 1, 2, 7, 20, 61, ... .

в). Арифметическая прогрессия: a₁=a, a_n+1=a_n+d, где a и d – заданные числа, d - разность арифметической прогрессии. Пусть a₁=5, d=0,7, тогда арифметическая прогрессия будет иметь вид:

5; 5,7; 6,4; 7,1; 7,8; 8,5; ... .

г). Геометрическая прогрессия: b₁= b, b_n+1= b_nq, где b и q – заданные числа, b 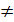0, q 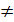0; q – знаменатель геометрической прогрессии. Пусть b₁=23, q=½, тогда геометрическая прогрессия будет иметь вид: 23; 11,5; 5,75; 2,875; ... .

3. Описательный способ

Правила задания последовательности описываются словами, без указания формул либо когда закономерность между элементами последовательности отсутствует.

Пример:

а). Рассмотрим последовательность натуральных четных чисел.

Из описания последовательности легко выписать ее члены:

2, 4, 6, 8, ...

б). Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, .... .

в). Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, ... .

г). Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16, ...

Вопрос 2. Основные свойства последовательностей

Рассмотрим два основных свойства последовательностей:

Первое свойство . Ограниченность последовательности

По виду ограниченности выделяются три вида последовательности:

А). Последовательность ( у _n ) называем ограниченной сверху, если все ее члены не больше некоторого числа М.

То есть последовательность ( у _n ) называем ограниченной сверху при у _n ≤ М.

Число М называем верхней границей последовательности.

Пример:

Последовательность у _n = 5 – n ограничена сверху.

При этом число М = 4.

Покажем, что при всех натуральных n должно выполняться неравенство у _n ≤ М.

В соответствии с условием, для любых n должны получить неравенство 5- n ≤ 4, из которого следует, что n ≥ 1 (то есть, неравенство справедливо при всех n ∈ N , где N –множество натуральных чисел).

Следовательно, при всех натуральных n неравенство выполняется.

Б). Последовательность (у _n ) называем ограниченной снизу, если все члены последовательности не меньше числа m.

То есть последовательность ( у _n ) называем ограниченной снизу при у _n ≥ m.

Число m называем нижней границей последовательности.

Пример:

Последовательность у _n = 3 + 2 n ограничена снизу.

При этом число m = 5 .

Покажем, что при всех натуральных n выполнено неравенство y_n ≥ m.

Получаем неравенство: 3 + 2 n ≥ 5, из которого следует, что n ≥1 (то есть неравенство справедливо при всех n ∈ N , где N –множество натуральных чисел).

В). Если последовательность (у _n ) ограничена и сверху, и снизу, то эту последовательность называем ограниченной последовательностью.

Или иначе: Последовательность (у _n ) называем ограниченной, если существуют два таких числа m и М , что для любого номера n выполняется неравенство m ≤ у _n ≤ М . (при n ∈ N , где N –множество натуральных чисел).

Пример :

Докажем ограниченность последовательности, которая выражена формулой: .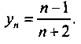

Найдем:

- первый (n =1) член последовательности у_1: 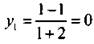и

- и член последовательности с очень большим номером n, например, у_100: .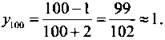

Возникает гипотеза, что последовательность ограничена, то есть m = 0 и М = 1.

Для этого необходимо доказать, что при всех натуральных значениях n выполняется неравенство .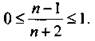

Очевидно, что левая часть неравенства выполняется.

Рассмотрим правую часть неравенства .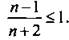

Так как выражение n + 2 положительно, то получим неравенство n - 1 ≤ n + 2 из которого следует, что -1 ≤ 2, что является верным.

Второе свойство . Монотонность последовательности

1. Последовательность (у _n ) называют возрастающей, если каждый член последовательности (начиная со второго) больше предыдущего, то есть у _n ₊₁ > у _n для n ≥ 1.

2. Последовательность (у _n ) называют убывающей, если каждый член последовательности (начиная со второго) меньше предыдущего, то есть y_n ₊₁ < у _n для n ≥ 1.

Пример:

Определим монотонность последовательности .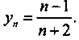

Запишем ( n +1)-й член последовательности:

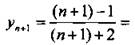
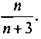Найдем разность двух соседних членов последовательности:

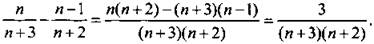Так как n – натуральное число, то при всех n полученная

дробь 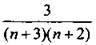положительна.

Поэтому у _n ₊₁ – у _n > 0, из чего следует, что

у _n ₊₁ > у _n при всех n (при n ∈ N , где N –множество натуральных чисел).

Из чего следует, что, по определению, данная последовательность (у _n ) – возрастающая.

Заметим, что возникает два случая:

1. Последовательность у _n = a_n при a >1 – возрастает;

2. Последовательность у _n = a_n при 0 < a < 1 – убывает.

Вопрос 3. Предел последовательности

Введем еще одно важнейшее понятие – предел последовательности.

Предел – это пространственная, временная или числовая граница чего-либо.

Число b называется пределом последовательности, если для всех достаточно больших n соответствующее значение y_n как угодно мало отличается от b .

или

Число b называем пределом последовательности (у _n ) , если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера N:

запишем с помощью условных обозначений: 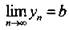, где значок lim – это значок предела;

прочитаем: предел последовательности, при стремлении n к бесконечности, равен b, при этом часто фразу «при стремлении n к бесконечности» опускаем.

Можно иначе: пишем: у _n → b,

читаем: у _n стремится к b, или у _n сходится к b.

Вспомним понятие «окрестность точки b». Под ним понимаем интервал ( b - r ; b + r ), где r – радиус окрестности (r >0).

Пример:

Покажем, что 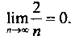(то есть, покажем, что предел числовой функции y_n = 2/ n – равняется нулю).

Прежде всего отметим, что понятие предела последовательности очень сложное и иногда воспринимается с трудом. Поэтому по пунктам разберем этот пример:

1). В данном случае число b = 0 (по определению, b – это значение предела последовательности: )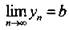

Выберем произвольный радиус r окрестности точки b (обычно r выбирают небольшим и r >0).

Поэтому будем рассматривать интервал (0- r ; 0+ r ) или (- r ; r ).

2). Нужно найти номер n, начиная с которого все члены последовательности у _n = 2/ n будут находиться в интервале (- r ; r ).

Чтобы найти этот номер n, надо относительно n решить неравенство

- r < 2/ n < r.

3). - Очевидно, что левая часть неравенства - r <2/ nвыполняется при всех натуральныхn.

- Решив правую часть неравенства 2/ n < r, получим 2< nr ,

откуда n > 2/ r .

Итак, при n > 2/ r все члены последовательности у _n отличаются от своего предела в менее чем на r.

4). Сделаем оценки. При r = 0,1 получаем n > 20 (то есть начиная с номера n = 21 все члены последовательности отличаются от предела не более чем на 0,1).

При r = 0,01 имеем n > 200 (то есть начиная с номера

n = 201 все члены последовательности отличаются от предела не более чем на 0,01) и т. д. На Рис. 2 приведена графическая иллюстрация для этого случая.

Рис.2

Видно, что в r-окрестности предела собирается (сгущается) бесконечное множество членов последовательности, вне этой окрестности находится только конечное число членов.

Итак,

- Если последовательность (у _n ) имеет предел, это означает что последовательность (у _n ) сходится и все члены этой последовательности сходятся к этому пределу. Последовательность называется сходящейся.

- Если последовательность (у _n ) не имеет предела, это означает что числовая последовательность (у _n ) расходится. Последовательность называется расходящейся.

Вопрос 4. Теоремы о пределах

Приведем формулировки теорем о пределах последовательностей.

Теорема 1. Если последовательность сходится, то только к одному пределу.

Теорема 2. Если последовательность сходится, то она ограничена.

Теорема 3. Если последовательность монотонна и ограничена, то она сходится.

Теорема 4. Если предел последовательности ( x_n ) равен b , а предел последовательности (у _n ) равен с, то есть то:

1) предел суммы этих последовательностей равен сумме пределов каждой из последовательностей: ;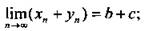

2) предел произведения последовательностей равен произведению пределов этих последовательностей: ;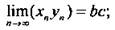

3) предел частного последовательностей равен частному пределов этих последовательностей: ;

4) постоянный множитель последовательности можно вынести за знак предела: .

Анализ

Дата добавления: 2021-06-02; просмотров: 114; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!