Методы статистической обработки данных

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Методами статистической обработки результатов называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе эксперимента, можно обобщать, приводить в систему, выявляя скрытые в них закономерности. Речь идет о таких закономерностях статистического характера, которые существуют между изучаемыми в эксперименте переменными величинами.

Данные – это основные элементы, подлежащие классифицированию или разбитые на категории с целью обработки.

Все методы математико-статистического анализа условно делятся на первичные и вторичные.

Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений.

Вторичными называются методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности.

К первичным методам статистической обработки относят, например:

– определение выборочной средней величины;

– выборочной дисперсии;

– выборочной моды;

– выборочной медианы.

В число вторичных методов обычно включают:

– корреляционный анализ;

– регрессионный анализ;

– методы сравнения первичных статистик у двух или нескольких выборок.

Методика обработки статистических данных в среде MathCAD

Рассмотрим регрессионный анализ, который относится ко вторичным методам статистической обработки данных.

Требуется произвести прогнозирование роста трафика по магистральным линиям связи на основе имеющихся статистических данных.

Суть регрессионного анализа заключается в нахождении наиболее важных факторов, которые влияют на зависимую переменную.

Создание регрессионной модели представляет собой итерационный процесс, направленный на поиск эффективных независимых переменных, чтобы объяснить зависимые переменные, которые мы пытаемся смоделировать или понять, запуская инструмент регрессии, чтобы определить, какие величины являются эффективными предсказателями.

Затем пошаговое удаление и/или добавление переменных до тех пор, пока не найдется наилучшим образом подходящая регрессионная модель. Так как процесс создания модели часто исследовательский, он никогда не должен становиться простым "подгоном" данных.

Процесс построения регрессионной модели должен учитывать теоретические аспекты, мнение экспертов в этой области и здравый смысл.

Линейная регрессия

Рассмотрим процесс построения регрессионной модели в среде MathCAD.

Статистические данные об объеме трафика по магистральным линиям связи за 9 лет для гипотетического участка приведены в таблице 1.

Таблица 1 – Исходные данные

год	квартал	Объем трафика	год	квартал	Объем трафика	год	квартал	Объем трафика
1	1	97,38	4	1	139,79	7	1	184,50
	2	89,45		2	114,67		2	188,04
	3	96,78		3	125,72		3	248,49
	4	100,31		4	144,23		4	198,16
2	1	106,36	5	1	78,91	8	1	277,48
	2	80,64		2	130,70		2	359,55
	3	110,93		3	164,91		3	286,03
	4	85,83		4	145,86		4	355,72
3	1	110,98	6	1	212,88	9	1	358,94
	2	137,98		2	102,17		2	400,24
	3	58,39		3	153,00		3	430,43
	4	94,69		4	168,44		4	523,52

В MathCAD по заданным векторам значений X и Y можно непосредственно найти коэффициенты регрессионной прямой Y=a 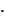X+b функциями intercept ("отрезок, отсекаемый с оси") и slope ("наклон").

Данные функции не предполагают, что данные отсортированы по возрастанию значений X, не предполагает этого и встроенный инструмент построения графиков, но без сортировки на больших размерностях пакет может тормозить, так что отсортируем пару векторов (X, Y) с помощью функции "csort".

Далее найдем коэффициенты a и b с помощью функций "intercept" и "slope".

Одним из показателей, описывающих качество построенной модели в статистике, является коэффициент детерминации (R^2), который ещё называют величиной достоверности аппроксимации. С его помощью можно определить уровень точности прогноза.

В зависимости от уровня коэффициента детерминации, принято разделять модели на три группы:

– 0,8 – 1 – модель хорошего качества;

– 0,5 – 0,8 – модель приемлемого качества;

– 0 – 0,5 – модель плохого качества.

В последнем случае качество модели говорит о невозможности её использования для прогноза.

Определим коэффициент детерминации с помощью функции: corr(f(X),Y1(X))².

В данном случае коэффициент детерминации при линейной регрессии равен kd=0,772, что характеризует выбранную модель, как модель приемлемого качества.

Листинг программы линейной регрессии приведен на рисунках 1, 2, 3.

Рисунок 1 – Листинг программы линейной регрессии

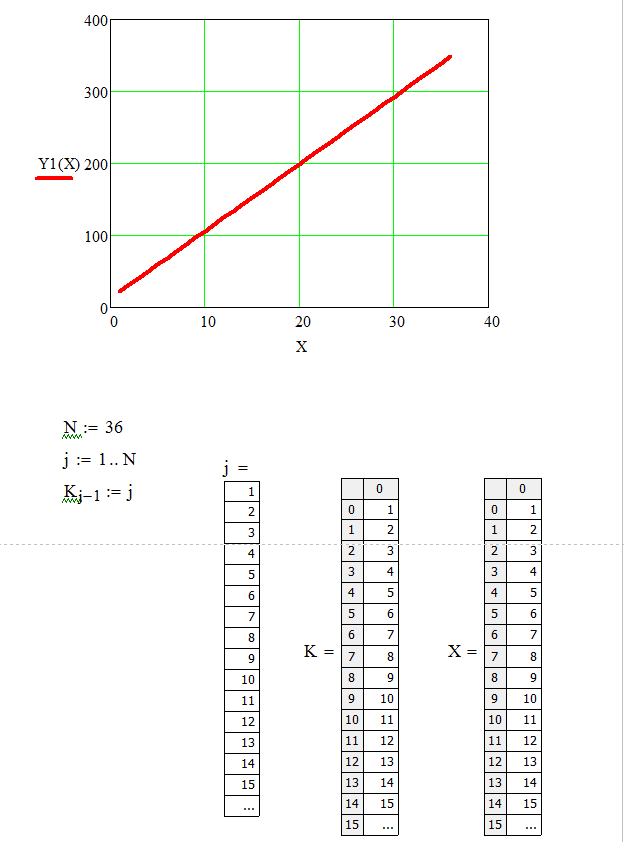
Рисунок 2 – Листинг программы линейной регрессии

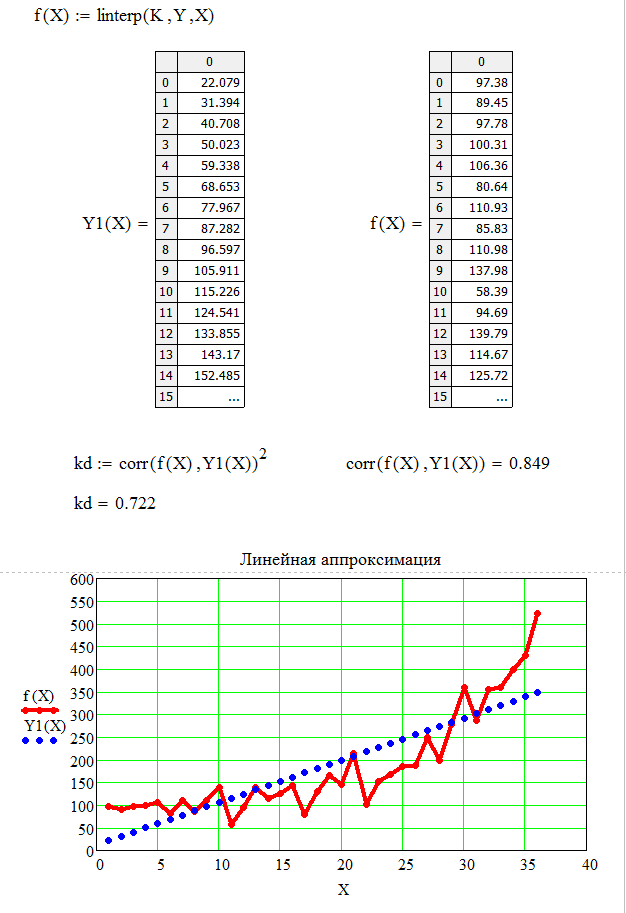
Рисунок 3 – Листинг программы линейной регрессии

Экспоненциальная регрессия

Для определения экспоненциальной функции решим систему (1) в MathCAD:

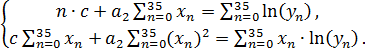(1)

Для этого с помощью значков суммирования векторов 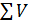и векторизации , находящихся на панели векторов и матриц, вычисляем: , , , .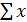

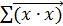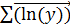Затем составляем матрицы А и B из соответствующих коэффициентов системы линейных уравнений (1) и находим решение системы с помощью встроенной функции "lsolve".

Решив систему (1), получим значения коэффициентов c и a₂.

Коэффициент a₁ вычисляем по формуле: a₁= .

Полученные значения коэффициентов используем в уравнение регрессии Y2(X)=a₁ .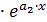

Вычислив параметры экспоненциальной регрессии, строим графики исходной функции и функции экспоненциальной регрессии Y2(X).

Определим коэффициент детерминации с помощью функции: corr(f(X),Y2(X))².

В данном случае коэффициент детерминации при экспоненциальной регрессии равен kd=0,859, что характеризует выбранную модель, как модель хорошего качества.

Листинг программы экспоненциальной регрессии приведен на рисунках 4, 5.

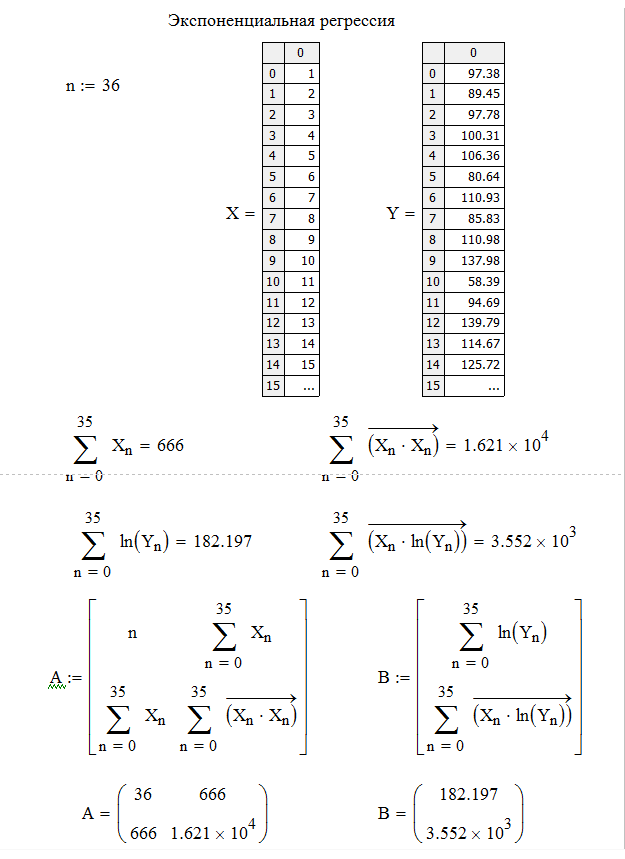
Рисунок 4 – Листинг программы экспоненциальной регрессии

Рисунок 5 – Листинг программы экспоненциальной регрессии

Логарифмическая регрессия

Для определения коэффициентов логарифмической функции воспользуемся встроенной функцией "lnfit(X, Y)".

Полученные значения коэффициентов используем в уравнение регрессии Y3(X)= .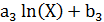

Вычислив параметры экспоненциальной регрессии, строим графики исходной функции f(x) и функции логарифмической регрессии Y3(X).

Определим коэффициент детерминации с помощью функции: corr(f(X),Y3(X))².

В данном случае коэффициент детерминации при логарифмической регрессии равен kd=0,423, что характеризует выбранную модель, как модель плохого качества и говорит о невозможности её использования для прогноза.

Листинг программы логарифмической регрессии приведен на рисунках 6, 7.

Рисунок 6 – Листинг программы логарифмической регрессии

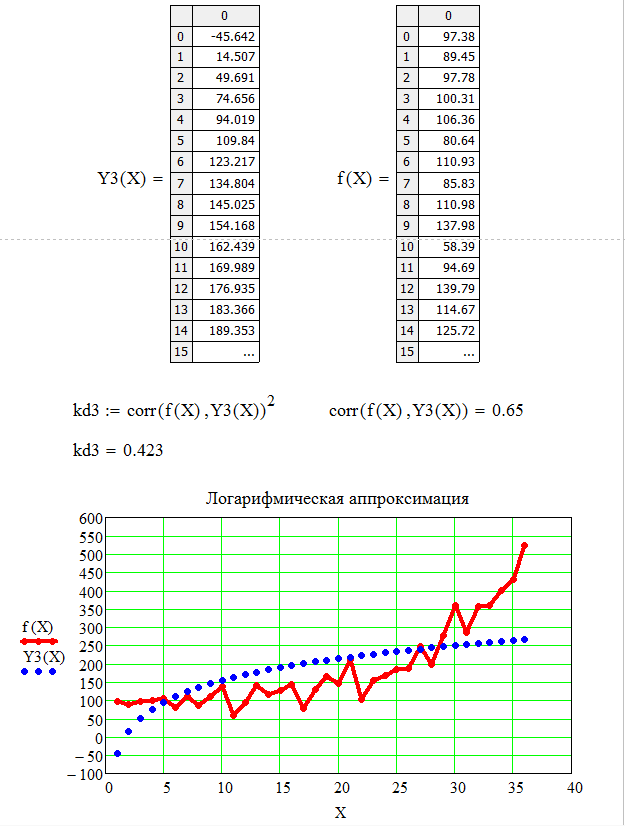
Рисунок 7 – Листинг программы логарифмической регрессии

Полиномиальная регрессия

Одномерная полиномиальная регрессия с произвольной степенью n полинома и с произвольными координатами отсчетов в MathCAD выполняется функцией "regress(X,Y,n)", которая вычисляет вектор S, в составе которого находятся коэффициенты полинома n-й степени. В нашем случае n=2.

Значения коэффициентов могут быть извлечены из вектора S функцией "submatrix(S, 3, длина(S)-1, 0, 0)".

Полученные значения коэффициентов используем в уравнении регрессии .

Вычислив параметры полиномиальной регрессии, строим графики исходной функции f(x) и функции логарифмической регрессии Y4(X).

Определим коэффициент детерминации с помощью функции: corr(f(X),Y4(X))².

В данном случае коэффициент детерминации при полиномиальной регрессии равен kd=0,916, что характеризует выбранную модель, как модель хорошего качества.

Листинг программы полиномиальной регрессии приведен на рисунках 8, 9.

Рисунок 8 – Листинг программы полиномиальной регрессии

Рисунок 9 – Листинг программы полиномиальной регрессии

Степенная регрессия

Для определения коэффициентов степенной функции воспользуемся встроенной функцией " pwfit(X, Y, g)", где g – вектор из трех элементов, задающий начальные значения коэффициентов С₀, С₁, С₂.

Полученные значения коэффициентов используем в уравнение регрессии .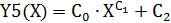

Вычислив параметры степенной регрессии, строим графики исходной функции f(x) и функции степенной регрессии Y5(X).

Определим коэффициент детерминации с помощью функции: corr(f(X),Y5(X))².

В данном случае коэффициент детерминации при степенной регрессии равен kd=0,94, что характеризует выбранную модель, как модель хорошего качества.

Листинг программы степенной регрессии приведен на рисунках 10, 11.

Рисунок 10 – Листинг программы степенной регрессии

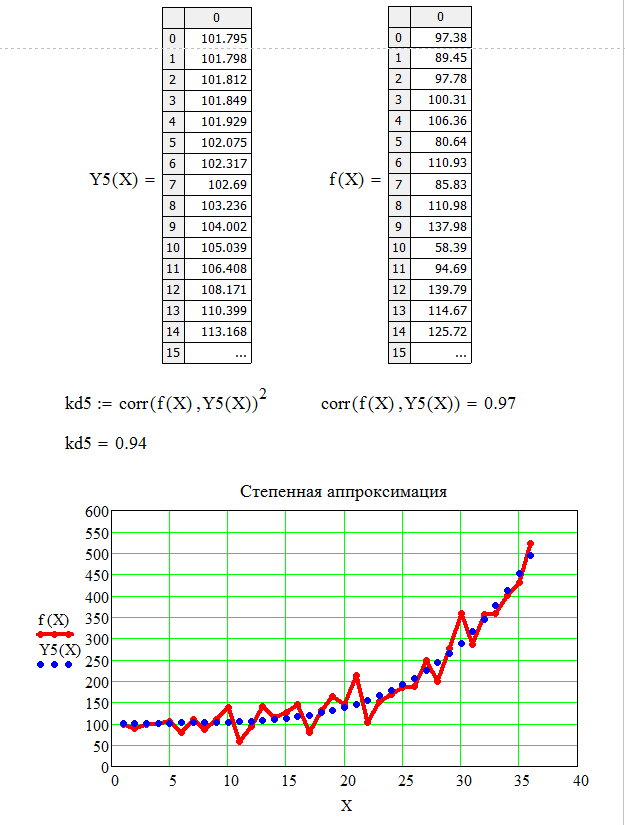
Рисунок 11 – Листинг программы степенной регрессии

График со всеми видами аппроксимации представлен на рисунке 12.

На оси X указывается число кварталов, а на оси Y – функции f(X), Y1(X), Y2(X), Y3(X), Y4(X), Y5(X).

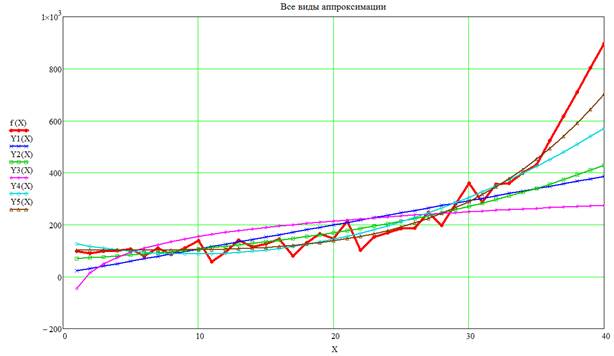
Рисунок 12 – График всех видов аппроксимации

На основе найденных статистических закономерностей определим ожидаемое значение объема трафика по магистральным линиям связи в период с 37 по 40 квартал т.е. на год вперед. Как видим на 40 квартале объем трафика составит 700 единиц, если использовать степенное уравнение регрессии.

График прогноза приведен на рисунке 13.

Рисунок 13 – График прогноза

Дата добавления: 2021-06-02; просмотров: 78; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!