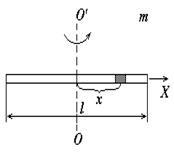
Гармонические колебательные движения и их характеристики
Колебания - процессы, обладающие той или иной степенью повторяемости во времени.
Гармоническими колебаниями называют такие периодически повторяющиеся движения материальной точки (тела), при которых ее смещение от положения равновесия изменяется по закону синуса или косинуса:
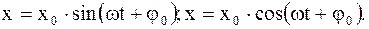 (1.19)
(1.19)
где x – смещение. Удаление материальной точки от положения равновесия в данный момент времени t;
x0- амплитуда колебаний. Наибольшее (максимальное) удаление материальной точки от положения равновесия;
(wt + j0) - фаза колебаний. Определяет положение материальной точки в данный момент времени t. Это периодически изменяющийся аргумент функции, описывающей колебательный или волновой процесс.
j0 - начальная фаза колебаний. Определяет положение материальной точки в начальный момент времени t = 0;
w = 2p/T = 2pn - круговая (циклическая) частота колебаний. Определяет число колебаний, совершаемых за время, t = 2p;
T - период колебаний. Время, за которое совершается одно полное колебание;
n - частота колебаний. Число колебаний, совершаемых в единицу времени.
Скорость материальной точки, совершающей гармоническое колебательное движение, - физическая величина, которая показывает, как изменяется смещение в единицу времени, численно равная первой производной от смещения по времени:
 (1.20)
(1.20)
Ускорение материальной точки, совершающей гармоническое колебание, - физическая величина, которая показывает, как изменяется скорость материальной точки в единицу времени, численно равная первой производной от скорости или второй производной от смещения по времени:
|
|
|
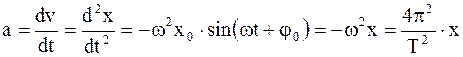 . (1.21)
. (1.21)
 Знак "минус" означает, что ускорение направлено в сторону, противоположную смещению.
Знак "минус" означает, что ускорение направлено в сторону, противоположную смещению.
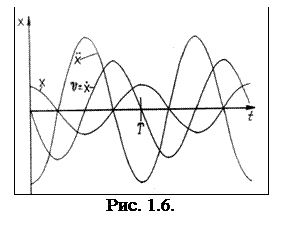
Из соотношений видно, что скорость имеет максимальное значение, когда точка проходит положение равновесия, а ускорение в крайних положениях.
Изменение смещения, скорости и ускорения с течением времени при гармонических колебательных движениях представлено на рис. 1.6
Динамика материальной точки и твёрдого тела
2.1. Основная задача динамики. Основные понятия и
определения. Классификация сил. Масса и импульс.
Динамика это раздел механики, в котором изучается движение тел и причины (силы), которые обусловливают тот или иной характер движения.
Первый закон Ньютон сформулировал так: "Всякое тело продолжается удерживаться в своем состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние".
Покой при этом рассматривается как частный случай равномерного прямолинейного движения со скоростью v = 0.
|
|
|
Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инерцией, а движение тела в этом случае - движением по инерции.
Изменение состояния движения означает, что тело приобретает ускорение. Воздействие одних тел на другие характеризуется физической величиной, называемойсилойF.
В общем случае сила определяется численным значением, направлением в пространстве и точкой приложения.
Сложение нескольких сил производится геометрически (по правилу параллелограмма, если силы направлены под углом друг к другу):
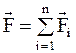 . (2.1)
. (2.1)
Все силы в механике можно разделить на:
а) фундаментальные, возникающие в отсутствие непосредственного контакта, которые обусловлены наличием полей у взаимодействующих тел (силы тяготения; силы электромагнитного взаимодействия и т.д.);
б) силы инерции, возникающие в неинерциальных системах отсчета;
в) молекулярные силы, силы взаимодействия молекул и атомов;
г) возникающие только при непосредственном взаимодействии тел (силы трения, упругие силы и т.д.);
В случае сил взаимного притяжения тел можно сказать, что любая масса 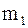 создает поле с напряженностью
создает поле с напряженностью  во всем окружающем пространстве и сила, притягивающая другую массу
во всем окружающем пространстве и сила, притягивающая другую массу  , равна
, равна
|
|
|
 . (2.2)
. (2.2)
По аналогии с электричеством можно записать
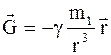 и
и 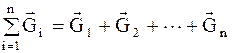 . (2.3
. (2.3
Существует несколько типов сил трения:
1) сила трения скольжения, обусловленная силами притяжения молекул двух тел, скользящих относительно друг друга;
2) сила вязкого трения, возникающая в результате медленного движения тела в жидкости или газе;
3) сила трения, вызванная быстрым движением тела в жидкости или газе.
Сила трения скольжения приводит к затратам энергии при перемещении тела по поверхности другого тела. Механизм потерь таков: неровности на поверхностях соприкасающихся тел при движении сминаются, возникают колебания и движения атомов, и тепло растекается по обоим телам.
Сила, нужная для того, чтобы преодолевать трение скольжения, пропорциональна нормальной силе с постоянным коэффициентом пропорциональности (коэффициентом трения):
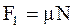 . (2.4)
. (2.4)
Сила вязкого трения оказывается пропорциональной 1-й степени скорости тела:
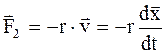 . (2.5)
. (2.5)
Сила трения, проявляющаяся при быстром движении тела в жидкости или газе, в отличие от простого вязкого трения обусловлена не только передачей импульса соседним слоям молекул жидкости или газа, но образованием в среде различных вихрей, звуковых и ультразвуковых волн, вибрациями самого тела. Однако приближенно эта сила пропорциональна квадрату скорости тела:
|
|
|
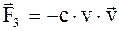 . (2.6)
. (2.6)
Физической величиной, характеризующей инертность материального тела, является его масса-m.
Одной из физических величин, описывающих свойства движущихся тел, является количество движения или импульс
p = mv. (2.7)
Обобщив опытные данные, Ньютон пришел к выводу: "Изменение количества движения пропорционально приложенной силе и направлено вдоль прямой, по которой действует данная сила".
Математически это можно записать так:
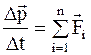 , (2.8)
, (2.8)
Выражение (2.9) называют основным уравнением движения материальной точки в динамике.
Из (2.9) следует, что при постоянной массе
a = F/m. (2.9)
Таким образом, ускорение всякого тела прямо пропорционально равнодействующей всех сил, приложенных к материальной точке и обратно пропорционально её массе.
Опыты показывают, что "всякое действие тел друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга взаимодействующие тела, всегда равны по величине и противоположны по направлению". Данное утверждение и носит название третьего закона Ньютона:
F12 = - F21. (2.10)
|
Рис.2.1 |
При этом силы действия и противодействия всегда приложены к разным телам и никогда не уравновешивают друг друга (рис.2.1).
Из основного уравнения динамики при v<<c
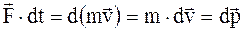 или
или  , (2.11)
, (2.11)
где 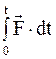 -импульс силы, мера действия силы за некоторый промежуток времени.
-импульс силы, мера действия силы за некоторый промежуток времени.
Импульс силы - векторная величина; он направлен, так же, как и действующая сила. При движении материальной точки (тела) под действием силы F ее количество движения получает приращение, равное импульсу силы. Понятие импульса широко используется в механике, в частности в теории удара, где величина, равная импульсу ударной силы за время удара, называется ударным импульсом.
Надо иметь в виду, что все законы динамики (классической механики) подтверждаются и проверяются опытным путем.
2.3. Элементы динамики материальной точки и твердого тела, совершающих вращательное движение
Основной задачей динамики вращательного движения является задача нахождения угловых ускорений, сообщаемых известными силами. Однако одна и та же сила, в зависимости от расстояния между ее направлением и осью вращения, сообщает различные угловые ускорения.
Для описания вращательного движения необходимо ввести новые физические величины: момент силы, момент инерции тела, момент импульсаМомент силы характеризует вращательный эффект силы при действии ее на твердое тело. Различают момент силы относительно центра (точки) и оси вращения.
Моментом силы относительно центра вращения называют векторную физическую величину, модуль которой равен произведению модуля силы на плечо:
çMç = çFç×l или M = F×ℓ, (2.11)
где l - плечо силы - кратчайшее расстояние от направления действия силы до центра вращения.
Вектор M направлен вдоль перпендикуляра к плоскости, на которой находится центр вращения и сила. Направление его определяется правилом правого винта. Так как
ℓ = r×sinα,
где r численное значение радиус-вектора r, который направлен из центра вращения в точку приложения силы;
α - угол между направлениями F и r,
то
M = F×r×sinα (2.12)
или в векторной форме
M = [r  F]. (2.13)
F]. (2.13)
Момент нескольких сил, имеющих одну точку приложения, равен алгебраической сумме моментов слагаемых сил:
 . (2.14)
. (2.14)
 Из третьего закона Ньютона следует, что моменты внутренних сил взаимодействия материальных точек системы относительно центра вращения попарно компенсируются. Следовательно, при вычислении главного момента сил необходимо учитывать только внешние силы, действующие на рассматриваемую механическую систему
Из третьего закона Ньютона следует, что моменты внутренних сил взаимодействия материальных точек системы относительно центра вращения попарно компенсируются. Следовательно, при вычислении главного момента сил необходимо учитывать только внешние силы, действующие на рассматриваемую механическую систему
|
 ,
,  .
. 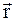 ,
, 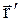 – радиус-вектора, проведенные из центра вращения в точку приложения силы.
– радиус-вектора, проведенные из центра вращения в точку приложения силы.
Разложим силу 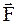 на плоскости на две составляющие – касательную и нормальную к окружности, по которой движется точка приложения силы:
на плоскости на две составляющие – касательную и нормальную к окружности, по которой движется точка приложения силы:
 . (2.15)
. (2.15)
Вращательное действие силы определяется только касательной составляющей силы и положением точки приложения силы по отношению к центру вращения, т.е. радиусом 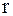 . Введем угол
. Введем угол  , образованный между направлениями векторов
, образованный между направлениями векторов 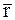 и
и 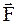 . Тогда получим
. Тогда получим
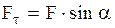 (2.16)
(2.16)
Вращательное действие любой силы будет пропорционально произведению:
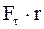 или
или  . (2.17)
. (2.17)
Выражение  представляет собой плечо силы, т.е. кратчайшее расстояние от линии действия силы до оси вращения.
представляет собой плечо силы, т.е. кратчайшее расстояние от линии действия силы до оси вращения.
По правилу "рычага" равновесие наступает при равенстве
 . (2.18)
. (2.18)
Произведение 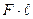 носит название момента силы относительно оси вращения
носит название момента силы относительно оси вращения 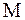 . Момент силы – это вектор, определяемый как векторное произведение:
. Момент силы – это вектор, определяемый как векторное произведение:
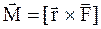 . (2.19)
. (2.19)
Модуль 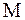 выражается следующим образом:
выражается следующим образом:
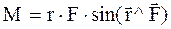 . (2.20)
. (2.20)
Этот вектор всегда перпендикулярен плоскости, образованной векторами 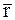 и
и 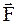 , т.е. направлен по оси вращения "по правилу правого винта".
, т.е. направлен по оси вращения "по правилу правого винта".
Для характеристики инертности тел (материальных точек) вращательному движению вводится в рассмотрение физическая величина, называемая моментом инерции материальной точки или тела (I относительно неподвижной оси (центра вращения). Чем больше 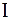 , тем меньше угловое ускорение e получит тело под действием данного момента силы
, тем меньше угловое ускорение e получит тело под действием данного момента силы 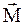 .
.
Моментом инерции материальной точки относительно какой-либо оси или центра вращения называется физическая величина, равная произведению массы материальной точки на квадрат расстояния от нее до оси или центра вращения:
DI = Dm×r2. (2.21)
Момент инерции тела - величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Прямой способ вычисления момента инерции тела состоит в следующем: мысленно тело разбивают на совокупность материальных точек, записывают момент инерции 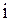 -й материальной точки, полный момент инерции получают суммированием элементарных моментов:
-й материальной точки, полный момент инерции получают суммированием элементарных моментов:
|
|
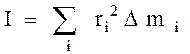 или
или 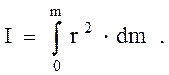 (2.22)
(2.22)
Рассмотрим несколько примеров:
|
Рис.2.4 |
1. Момент инерции обруча, вращающегося вокруг собственной оси (рис.2.3). Обруч считаем "тонким" и однородным по плотности. В данном случае все материальные точки (элементарные массы) расположены на одинаковом расстоянии от оси вращения. Поэтому
 . (2.23)
. (2.23)
2. Момент инерции стержня относительно оси, проходящей перпендикулярно к нему через его середину (рис.2.4). Стержень считаем "тонким", однородным по сечению и распределению плотности. Длина стержня – 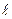 . Момент инерции материальной точки представим в виде дифференциала
. Момент инерции материальной точки представим в виде дифференциала
 (2.24)
(2.24)
где  – площадь сечения.
– площадь сечения.
|
Рис.2.5 |
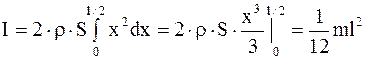 . (2.25)
. (2.25)
|
Рис.2.6 |
Таким образом, момент инерции тела существенно зависит от его геометрии (формы), а также от положения оси вращения.
Значительное упрощение в вычислениях момента инерции тела относительно оси, не проходящей через центр масс этого тела, можно получить, применяя теорему Штейнера, формулировку которой мы примем без доказательства (рис.2.6): «Момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс тела, I0 и произведения массы тела m0 на квадрат расстояния между осями», т.е.
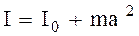 . (2.26)
. (2.26)
Дата добавления: 2021-05-18; просмотров: 115; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

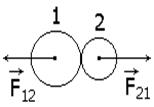
 Рис.2.3
Рис.2.3