Элементы кинематики материальной точки и тела, совершающих вращательное движение.
ЛЕКЦИЯ №1
ЭЛЕМЕНТЫ КИНЕМАТИКИ И ДИНАМИКИ
Пран лекции
1. Механика и ее разделы. Физические модели: материальная точка (частица), абсолютно твердое тело
2. Элементы кинематики тела, совершающего вращательное движение
3. Гармонические колебательные движения и их характеристики
Механика и ее разделы. Физические модели: материальная точка (частица), абсолютно твердое тело
Механика – раздел физики, в котором изучается простейшая форма движения - механическое движение, причины вызывающие это движение и происходящие при этом взаимодействия между телами.
Механическое движение - изменение с течением времени взаимного положения тел или их частей (частиц) в пространстве. В соответствии с характером решаемых задач механику подразделяют на следующие разделы: 1) кинематику; 2) динамику; 3) статику.
Кинематика изучает геометрические свойства движения и взаимодействия тел в не связи с порождающими их причинами.
1. Материальная точка - объект малых размеров (размерами, которого в условиях данной задачи можно пренебречь).
2. Абсолютно твердое тело - тело, расстояние между двумя любыми точками которого всегда остается неизменным. Применимо, когда можно пренебречь деформацией тела;
2. Системы отсчета и описание движений. Элементы кинематики материальной точки: перемещение, скорость и ускорение
Известно, что кинематика - это раздел механики, в котором изучаются движения и взаимодействия тел без указания порождающих их их причин. Произвольно выбранное, условно неподвижное тело, по отношению к которому рассматривается движение данного тела, называют телом отсчета.
|
|
|
Связанная с телом отсчета произвольная система координат, с устройством измерения времени называется системой отсчета.
|
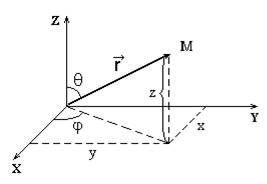
Рис.1.1 |
На рис. 1.1 показана прямоугольная (декартова) система координат.
Положение материальной точки (тела) в прямоугольной системе отсчета, в данный момент времени, может быть определено тремя способами: 1) с помощью координат x, y, z - M(x,y,z). В этом случае говорят, что материальная точка обладает тремя степенями свободы; 2) с помощью радиус - вектора r; 3) естественным (траекторным), который применяется обычно тогда, когда известна траектория движения точки по отношению к выбранной системе отсчета. В этом случае зависимость S = f(t) может быть задана графически либо в виде таблицы. При этом указанные способы равноправны.
Между координатами x, y, z и проекциями радиус-вектора r существует связь:
x = rx, y = ry, z = rz. 
(1.1)
С течением времени может произойти изменение положения материальной точки (тела) в пространстве (изменение ее координат), тогда можно записать:
|
|
|
x = f1(t); y = f2(t); z = f3(t); (1.2)
Записанные выражения являются уравнениями движения материальной точки (тела) в кинематике.
Положение материальной точки в полярной системе координат задается радиус-вектором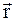 
, который имеет определенный модуль r, и углами q и j, которые он составляет с осями декартовой системы координат.
Простейшим видом механического движения тела является поступательное движение. Это такое движение, при котором прямая, проведённая через любые две точки тела перемещается параллельно самой себе.
При этом все точки тела описывают одинаковые траектории, смещенные относительно друг друга. Рассматривая движение отдельных точек, можно установить характер движения тела.
Для характеристики движения материальной точки вводятся следующие основные понятия и определения.
Перемещение - вектор, проведенный из начального положения материальной точки (тела) в ее положение в данный момент времени (отрезок, соединяющий последовательные положения материальной точки или тела) - приращение радиус-вектора r за рассматриваемый промежуток времени
Dr = r – rо. (1.4)
|
|
|
|
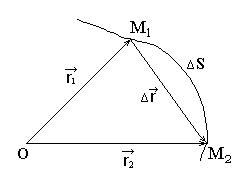
Рис.1.2 |
Перемещение характеризуется не только численным значением, но и направлением в пространстве. На рис.1.2 D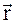 
– вектор перемещения точки за промежуток времени Dt: 
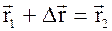или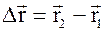 
; DS – пройденный за это время путь.
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения численно равен пройденному пути:
½Dr½ = DS (1.5)
Расстояние - модуль перемещения. Расстояние, пройденное телом при его движении по траектории, - путь. В частных случаях перемещение и путь могут совпадать.
За одни и те же промежутки времени перемещение точки может быть разным. Если положение точки в пространстве в какой-то момент времени t определить вектором r(t), а в момент времени t + Dt - (r + Dr), то за время (t2 – t1) = Dt она совершает перемещение Dr. При этом отношение Dr/Dt зависит от Dt. Однако при уменьшении Dt эта зависимость становится менее явной, и при Dt®0 оно стремится к некоторому пределу. Предел отношения Dr/Dt при Dt®0 называют мгновенной скоростью.
Таким образом, мгновенная линейная скорость - векторная физическая величина, характеризующая состояние движения, показывающая, как изменяется перемещение в единицу времени, численно равная первой производной от перемещения по времени:
|
|
|
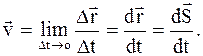(1.3)
Средняя скорость неравномерного движения - скалярная физическая величина, численно равная отношению всего пути, пройденного телом (материальной точкой), к тому промежутку времени, в течение которого совершалось движение:
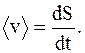(1.4)
Важной задачей кинематики является нахождение пройденного материальной точкой пути. Известно, что при прямолинейном равнопеременном движении
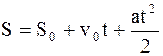. Согласно (2.6), 
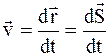, следовательно
dS = v ×dt. (1.5)
При небольших промежутках времени Dt можно считать, что элементарный путь dS численно равен ½dr½, причем при уменьшении промежутка времени точность совпадения числовых значений пути и перемещения возрастает.
|
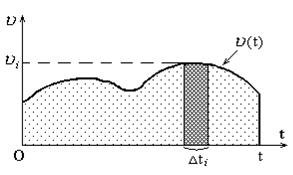
Рис.1.3 |
Поэтому путь, пройденный материальной точкой при неравномерном движении за промежуток времени от t1 до t2, можно определить по формуле
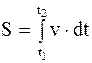. (1.6)
Таким образом, величина пути определяется криволинейным интегралом.
Путь численно равен площади фигуры, ограниченной кривой зависимости v = f(t) и прямыми t = t1,
t = t2 и осью времени на графике скорости (рис.1Отношение изменения скорости Dv к промежутку времени Dt, в течение которого оно происходит, зависит от величины Dt, однако при его уменьшении эта зависимость становится менее явной, и при Dt®0 оно стремится к пределу, который называют линейным ускорением:
. (1.7)
Следовательно, линейное ускорение - векторная физическая величина, характеризующая изменение скорости в единицу времени, численно равная первой производной от скорости или второй производной от перемещения по времени.
Можно разложить вектор линейного ускорения на две составляющие по направлению линейной скорости - вдоль касательной к траектории движения. Эту составляющую линейного ускорения называют тангенциальным ускорением – аt. Тангенциальное ускорение характеризует изменение линейной скорости по величине:
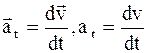. (1.8)
Составляющую линейного ускорения, направленную по нормали n к вектору линейной скорости, т.е. к касательной в данной точке, называют нормальным ускорением - an. Нормальное ускорение характеризует изменение линейной скорость по направлению:
, 
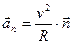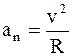(1.9
где R - радиус кривизны траектории движения;
n - единичный вектор нормали к траектории движения.
Полное ускорение a можно определить как
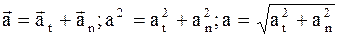. (1.10)
Таким образом, направление тангенциального ускорения направлено по касательной к траектории в данной точке, а направление нормального ускорения перпендикулярно направлению линейной скорости.
При неравномерном движении величину
(1.11)
Элементы кинематики материальной точки и тела, совершающих вращательное движение.
|
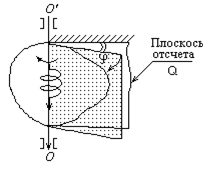
Рис.1.4 |
Вращательным движением твердого тела вокруг неподвижной оси называют такое движение, при котором какие-либо две его точки остаются неподвижнымив процессе движения. Прямая, проходящая через эти точки, называется осью вращения; все остальные точки твердого тела при вращательном движении описывают окружности в плоскостях, перпендикулярных к оси вращения, центры которых лежат на этой оси (рис.1.4).
Угол поворота j - угол между проведенными через ось вращения неподвижной полуплоскостью (плоскостью отсчета) и полуплоскостью, жестко связанной с телом и вращающейся вместе с ним. Угол поворота - псевдовектор - вектор, численно равный углу между двумя положениями радиуса R, направленный вдоль оси вращения и связанный с направлением вращения правилом векторного произведения (правилом правого винта).
Угловая скорость w - векторная физическая величина, показывающая, как изменяется угол поворота j в единицу времени, численно равная первой производной от угла поворота по времени:
. (1.12)
Вектор угловой скорости направлен вдоль оси вращения в сторону, определяемую правилом правого винта (векторного умножения).
При равномерном вращении ω = const, ω = φ/t. Равномерное вращательное движение характеризуется периодом, частотой вращения и циклической или круговой частотой.
Период (T) - время, в течение которого тело сделает один полный оборот.
Частота (n) - число оборотов, совершаемых в единицу времени.
Круговая (циклическая) частота ω - число оборотов, совершаемых за время, равное 2π. Между периодом, частотой и круговой частотой имеется связь:
ω = 2πn = 2π/T; n = 1/T. (1.13)
Угловая скорость может изменяться как по величине, так и по направлению.
Векторная физическая величина, характеризующая изменению угловой скорости в единицу времени, численно равная первой производной от угловой скорости по времени или второй производной от угла поворота по времени, называется угловым ускорением
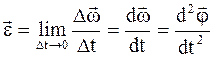. (1.14)
Точка, находящаяся на расстоянии r от оси вращения, двигаясь по траектории (окружности), проходит путь (рис.1.5):
|
Рис.1.5 |
DS = r×Dj. (1.15)
v = r×ω. (1.16)
v = r×ω sinα или v =[ω×r]. (1.17)
Известно, что a2 = at2 + an2, где at = dv/dt, an = v2/r. Следовательно, связь между полным линейным ускорением, тангенциальным и нормальным ускорениями имеет вид:
(1.18)
Дата добавления: 2021-05-18; просмотров: 136; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!