Свертка функций и ее свойства
Сверткой  двух функций
двух функций  и
и 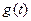 называется интеграл
называется интеграл
 . (25)
. (25)
Свертка не зависит от порядка, в котором расположены функции
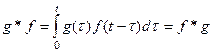 (26)
(26)
Доказательство.

Пример 11.
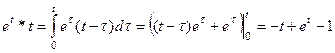 .
.
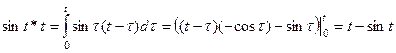
Если функции  и
и 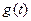 являются оригиналами, то их свертка также является оригиналом:
являются оригиналами, то их свертка также является оригиналом:
1) 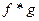 обращается в нуль при
обращается в нуль при  , так как
, так как 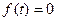 и
и 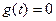 при
при  ;
;
2) 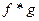 кусочно-непрерывна при
кусочно-непрерывна при 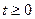 , так как
, так как  и
и 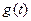 кусочно-непрерывны при
кусочно-непрерывны при 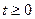 ;
;
3) 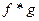 имеет конечную степень роста
имеет конечную степень роста
Пусть  ,
, 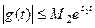 для
для  . Тогда
. Тогда 
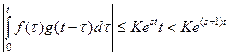 , так как
, так как 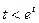 при всех значениях
при всех значениях 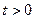 .
.
9. Теорема об умножении изображений.
Если 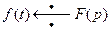 и
и 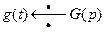 , то
, то
 . (27)
. (27)
Доказательство.
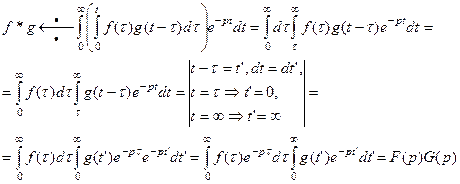
На рисунке заштрихована область интегрирования для двойного интеграла, для которой легко получить пределы интегрирования соответствующих повторных интегралов.

Интеграл Дюамеля.
Найдем оригинал, соответствующий произведению 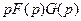 .
.

Здесь были использованы теорема умножения изображений и свойство линейности преобразования Лапласа.
Следовательно,
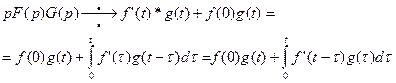 (28)
(28)
Аналогично
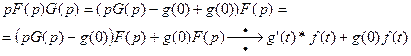 (29)
(29)
Тогда
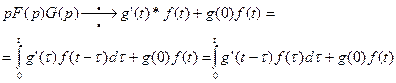 (30)
(30)
Правые части в равенствах (28) и (30), содержащие интегралы, называются интегралами Дюамеля.
Обращение преобразования Лапласа.
Теорема Меллина.
Если аналитическая в области 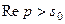 функция
функция  является изображением кусочно-гладкой на каждом конечном отрезке луча
является изображением кусочно-гладкой на каждом конечном отрезке луча 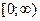 функции
функции  с показателем роста
с показателем роста 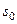 , то
, то
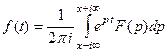 . (32)
. (32)
В этой формуле путь интегрирования – любая прямая  , параллельная мнимой оси, лежащая правее прямой
, параллельная мнимой оси, лежащая правее прямой 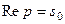 .
.
|
|
|
Непосредственное применение формулы (32) для отыскания оригинала по заданному изображению часто вызывает затруднения. Поэтому обычно пользуются теоремами разложения, которые являются следствиями из нее.
Первая теорема разложения. Если разложение функции  в ряд по степеням
в ряд по степеням 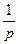 имеет вид
имеет вид 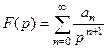 , то оригиналом является функция
, то оригиналом является функция 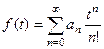 , где
, где 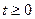 , (
, ( 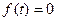 при
при  ).
).
Вторая теорема разложения. Если 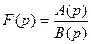 -рациональная функция, где
-рациональная функция, где 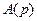 и
и 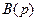 - многочлены, причем 1) степень многочлена
- многочлены, причем 1) степень многочлена 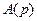 меньше степени многочлена
меньше степени многочлена 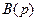 , 2)
, 2) 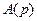 и
и 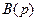 не имеют общих корней, т.е. дробь
не имеют общих корней, т.е. дробь  несократима, то оригинал
несократима, то оригинал  , соответствующий функции
, соответствующий функции  , имеет вид
, имеет вид
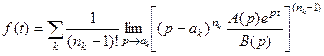 , (33)
, (33)
где  - нули знаменателя
- нули знаменателя  , а
, а  - их кратность. В правой части вычисляется предел от производной порядка
- их кратность. В правой части вычисляется предел от производной порядка  по комплексной переменной
по комплексной переменной  при постоянном
при постоянном  .
.
В том случае, когда знаменатель  – многочлен степени, который имеет только простые корни, формула (33) упрощается
– многочлен степени, который имеет только простые корни, формула (33) упрощается
 (34)
(34)
10. Теорема об умножении оригиналов: если  и
и 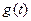 являются оригиналами с показателями роста
являются оригиналами с показателями роста 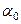 ,
, 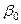 соответственно и
соответственно и 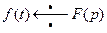 ,
, 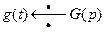 , то произведение
, то произведение 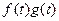 является оригиналом с показателем роста
является оригиналом с показателем роста 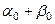 и справедливо соотношение
и справедливо соотношение
|
|
|
 (35)
(35)
где 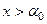 ,
, 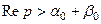 .
.
При восстановлении оригинала по заданному изображению часто приходится решать задачу представления правильной рациональной дроби в виде суммы простейших дробей.
Представление правильной рациональной дроби в виде суммы
Простейших дробей
Рациональной дробью  называется отношение двух многочленов
называется отношение двух многочленов
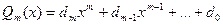 (36)
(36)
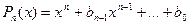 ( 37)
( 37)
Рациональная дробь  называется правильной, если степень
называется правильной, если степень 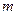 многочлена
многочлена 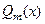 меньше степени
меньше степени 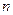 многочлена
многочлена 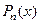 , т.е.
, т.е. 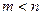 . Если дробь неправильная, то можно разделить числитель на знаменатель и выделить многочлен и правильную дробь.
. Если дробь неправильная, то можно разделить числитель на знаменатель и выделить многочлен и правильную дробь.
Любой многочлен степени 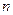 имеет
имеет 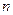 корней, среди которых могут быть вещественные корни и комплексные корни. Многочлен с вещественными коэффициентами наряду с каждым комплексным корнем вида
корней, среди которых могут быть вещественные корни и комплексные корни. Многочлен с вещественными коэффициентами наряду с каждым комплексным корнем вида 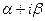 имеет комплексно сопряженный корень вида
имеет комплексно сопряженный корень вида 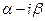 . Многочлен
. Многочлен 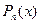 может быть представлен в виде линейных относительно
может быть представлен в виде линейных относительно 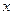 множителей вида
множителей вида 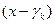 , где
, где 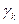 – вещественный или комплексный корень, т.е.
– вещественный или комплексный корень, т.е.
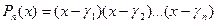 (38)
(38)
Объединим в произведении (38) множители, соответствующие комплексно сопряженным корням вида 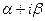 и
и 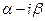 . Тогда получим
. Тогда получим
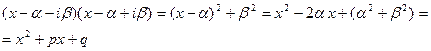 ,
,
где введены обозначения 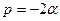 ,
, 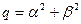 . При этом
. При этом 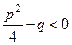 , что означает, что многочлен
, что означает, что многочлен 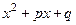 имеет комплексные корни.
имеет комплексные корни.
|
|
|
Среди корней многочлена могут быть одинаковые корни, т.е. некоторые корни могут иметь кратность, отличную от 1. Тогда разложение многочлена на множители будет иметь вид
 (39)
(39)
где 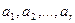 –-вещественные корни кратности
–-вещественные корни кратности 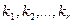 соответственно, остальные корни являются комплексными корнями кратности
соответственно, остальные корни являются комплексными корнями кратности 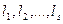 соответственно, при этом
соответственно, при этом  .
.
Простейшими дробями называются правильные рациональные дроби вида
 ;
; 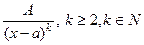 ;
; 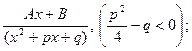
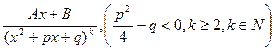 .
.
Любую правильную рациональную дробь вида  можно представить в виде суммы простейших дробей.
можно представить в виде суммы простейших дробей.
Если знаменатель дроби представлен в виде разложения
 (40)
(40)
где 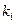 и
и 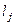 - кратности соответствующих вещественных и комплексных корней, то разложение правильной рациональной дроби на простейшие будет иметь вид
- кратности соответствующих вещественных и комплексных корней, то разложение правильной рациональной дроби на простейшие будет иметь вид
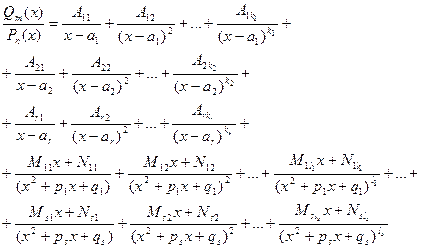 (41)
(41)
Для нахождения коэффициентов разложения 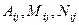 нужно умножить обе части равенства (41) на многочлен
нужно умножить обе части равенства (41) на многочлен 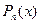 . В результате получится тождественное равенство двух многочленов, из которого значения
. В результате получится тождественное равенство двух многочленов, из которого значения 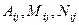 находят, приравнивая коэффициенты при одинаковых степенях
находят, приравнивая коэффициенты при одинаковых степенях 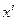 в левой и правой частях равенства, либо используют метод частных значений.
в левой и правой частях равенства, либо используют метод частных значений.
Таблица оригиналов и изображений
| № | Оригинал 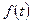
| Изображение 
|
| 1 | 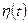
| 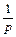
|
| 2 | 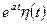
| 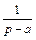
|
| 3 | 
| 
|
| 4 | 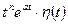
| 
|
| 5 | 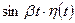
| 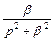
|
| 6 | 
| 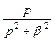
|
| 7 | 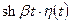
| 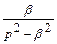
|
| 8 | 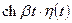
| 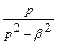
|
| 9 | 
| 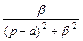
|
| 10 | 
| 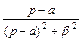
|
| 11 | 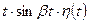
| 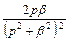
|
| 12 | 
| 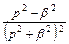
|
| 13 | 
| 
|
|
|
|
Дата добавления: 2021-05-18; просмотров: 79; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
