Свойства преобразований Лапласа
Основы операционного исчисления
Лекция 1
Преобразование Лапласа и его свойства
Операционное исчисление применяется при нахождении как частных, так и общих решений линейных дифференциальных уравнений любого порядка с постоянными коэффициентами, при этом правая часть уравнения на различных интервалах может быть задана различными аналитическими выражениями, а также может иметь точки разрыва. Операционный метод используется для решения однородных и неоднородных систем дифференциальных уравнений, причем правые части неоднородных систем также могут быть заданы на различных интервалах различными аналитическими выражениями и иметь точки разрыва первого рода.
Операционное исчисление широко применяется для решения задач электротехники и теории автоматического управления и регулирования, в частности позволяет найти установившийся ток в колебательном контуре при периодическом и непериодическом внешнем напряжении. Операционные методы позволяют рассчитывать процессы в сложных электрических цепях при произвольном внешнем напряжении. Операционные методы позволяют также находить решения уравнений в частных производных, которые появляются в задачах математической физики, например при решении задачи о колебательном движении струн и стержней, о распространении тепла в стержне, плоских пластинах и пространственных телах, о распространении электрических колебаний вдоль длинных цепей.
|
|
|
Операционное исчисление строится на основе преобразования Лапласа.
Преобразованием Лапласа или изображением по Лапласу функции  вещественной переменной
вещественной переменной  называется функция
называется функция  комплексной переменной
комплексной переменной 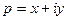 , определяемая несобственным интегралом
, определяемая несобственным интегралом
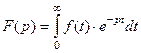 . (1)
. (1)
Интегралом Лапласа называется интеграл в правой части (1).
Оригиналом называется функция вещественной переменной  , которая удовлетворяет условиям:
, которая удовлетворяет условиям:
1) 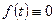 при
при  ,
,
2)  кусочно-непрерывна при
кусочно-непрерывна при 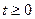 ; это означает, что функция
; это означает, что функция  может иметь на каждом отрезке при
может иметь на каждом отрезке при 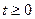 лишь конечное число точек разрыва первого рода;
лишь конечное число точек разрыва первого рода;
3)  имеет ограниченную степень роста:
имеет ограниченную степень роста:  при любом
при любом  , где
, где  некоторые постоянные числа. Число
некоторые постоянные числа. Число 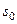 называется показателем роста функции
называется показателем роста функции  или абсциссой сходимости интеграла Лапласа.
или абсциссой сходимости интеграла Лапласа.
Иногда преобразованием Лапласа называется операция перехода от оригинала  к изображению
к изображению  . Соответствие между функциями
. Соответствие между функциями  и
и  записывается в виде
записывается в виде 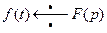 .
.
Если функция  является оригиналом, то интеграл Лапласа сходится абсолютно и равномерно на комплексной полуплоскости
является оригиналом, то интеграл Лапласа сходится абсолютно и равномерно на комплексной полуплоскости  .
.
Доказательство. Пусть 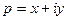 , и
, и 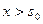 . Тогда
. Тогда 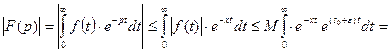
 . Отсюда следует, что интеграл Лапласа сходится абсолютно при
. Отсюда следует, что интеграл Лапласа сходится абсолютно при 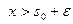 , так как он мажорируется абсолютно сходящимся интегралом. Если же
, так как он мажорируется абсолютно сходящимся интегралом. Если же 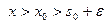 , то
, то  , где в правой части неравенства получено число. Следовательно, интеграл Лапласа сходится равномерно при
, где в правой части неравенства получено число. Следовательно, интеграл Лапласа сходится равномерно при 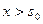 .
.
|
|
|

Преобразование Лапласа устанавливает связь между оригиналами  и их изображениями. Определенным действиям, производимым над оригиналами, соответствуют некоторые действия, производимые над их изображениями, причем действия над изображениями оказываются более простыми, чем над оригиналами. В частности, дифференциальному уравнению относительно оригинала соответствует алгебраическое уравнение относительно изображения. Если решить это алгебраическое уравнение и затем найти оригинал полученного решения, то тем самым будет получено решение исходного дифференциального уравнения.
и их изображениями. Определенным действиям, производимым над оригиналами, соответствуют некоторые действия, производимые над их изображениями, причем действия над изображениями оказываются более простыми, чем над оригиналами. В частности, дифференциальному уравнению относительно оригинала соответствует алгебраическое уравнение относительно изображения. Если решить это алгебраическое уравнение и затем найти оригинал полученного решения, то тем самым будет получено решение исходного дифференциального уравнения.
Единичной функцией Хевисайда называется функция  . График функции Хевисайда имеет вид
. График функции Хевисайда имеет вид

Для функции Хевисайда используются также следующие обозначения:  ,
, 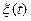 ,
, 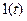 ,
,  ,
, 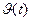 ,
,  .
.
Пример 1. Найти изображение единичной функции Хевисайда.
 ,
, 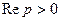
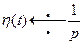
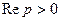 (3)
(3)
Условимся в дальнейшем под функцией  понимать функцию, которая равна нулю при
понимать функцию, которая равна нулю при  , т.е.
, т.е.  .
.
Пример 2. Найти изображение показательной функции 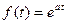 .
.
|
|
|
 для
для  .
.
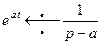
 (4)
(4)
Пример 3. Найти изображение степенной функции  ,
,  и
и 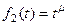 ,
, 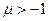 .
.
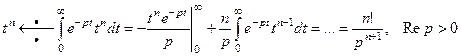
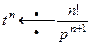
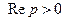 (5)
(5)
Свойства преобразований Лапласа
1. Свойство линейности: если 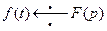 и
и  , то
, то
 . (6)
. (6)
Используя это свойство и соотношение (4), найдем изображение тригонометрических и гиперболических функций

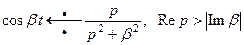 (7)
(7)

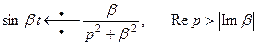 (8)
(8)
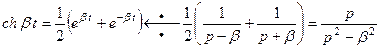
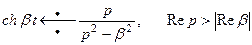 (9)
(9)
Аналогично
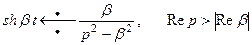 (10)
(10)
2. Теорема подобия. Для любого 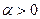
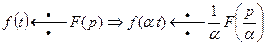
 . (11)
. (11)
Доказательство 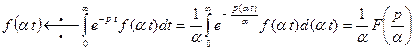
3. Теорема смещения: умножение оригинала на множитель 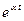 приводит к смещению аргумента изображения на
приводит к смещению аргумента изображения на 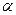 .
.
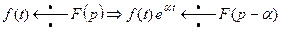 ,
,  .(12)
.(12)
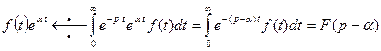
Пример 4.
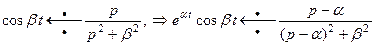 (13)
(13)
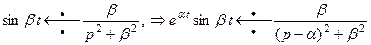 (14)
(14)
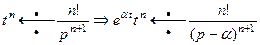 (15)
(15)
4. Теорема запаздывания: включению оригинала с запаздыванием на  соответствует умножение изображения на
соответствует умножение изображения на 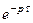 .
.
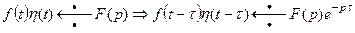
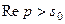 (16)
(16)
Доказательство. Рассмотрим функцию  , тогда
, тогда
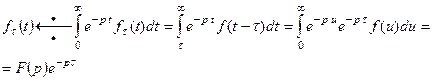
Функцию  можно представить в виде
можно представить в виде 
 и тогда
и тогда  .
.
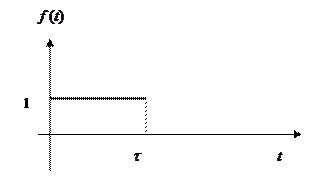
Пример 5. Найти изображение функции 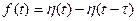 , которая представляет собой единичный импульс, действующий в течение промежутка времени
, которая представляет собой единичный импульс, действующий в течение промежутка времени 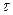 .
.
 На рисунке представлен график функции
На рисунке представлен график функции  .
.
|
|
|
Учитывая соотношение (3), в соответствии с теоремой запаздывания получим
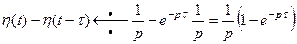 .
.
Пример 6. Найти изображение функции 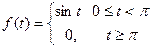
Представим эту функцию с помощью функции Хевисайда в виде 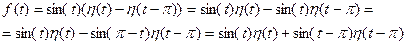
Здесь были использованы формулы приведения 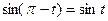 и нечетность функции синуса. В соответствии с формулой (8)
и нечетность функции синуса. В соответствии с формулой (8) 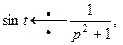 тогда по теореме запаздывания
тогда по теореме запаздывания 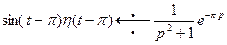 . Отсюда для исходной функции получим изображение
. Отсюда для исходной функции получим изображение 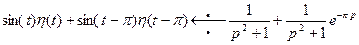 .
.
Пример 7. Найти изображение функции  .
.
Запишем функцию  с помощью функции Хевисайда в виде
с помощью функции Хевисайда в виде 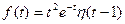 . Преобразуем эту функцию к функции аргумента
. Преобразуем эту функцию к функции аргумента 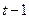 . Очевидно, что
. Очевидно, что  . Тогда
. Тогда 
Учитывая, что в соответствии с (5) 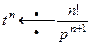 , получим
, получим 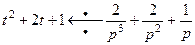 . Отсюда по теореме смещения
. Отсюда по теореме смещения
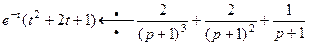 . Применяя теперь теорему запаздывания, получим
. Применяя теперь теорему запаздывания, получим
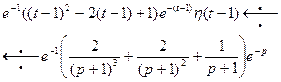
Пример 8. Найти оригинал для функции 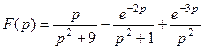 .
.
Учитывая, что в соответствии с формулами (7), (8), и (5) 
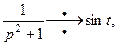
 , получим по теореме запаздывания
, получим по теореме запаздывания 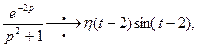 .
. 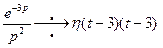 , Тогда
, Тогда
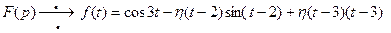 . Следовательно, функцию
. Следовательно, функцию  можно записать в виде
можно записать в виде
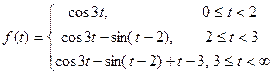
5. Теорема о дифференцировании оригинала:
Если 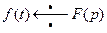 и функции
и функции 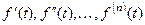 являются оригиналами, то
являются оригиналами, то
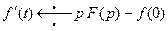 , (17)
, (17)
 (18)
(18)
………………………………………………..
 (19)
(19)
В частности, если  , то
, то
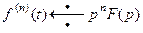 . (20)
. (20)
Доказательство. 
Здесь было использовано интегрирование по частям при обозначениях 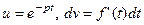 . Поскольку
. Поскольку 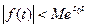 , то
, то 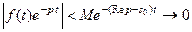 при
при 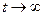 , если
, если 
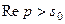 . Поэтому неинтегральный член дает вклад в результат
. Поэтому неинтегральный член дает вклад в результат 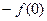 .
.
Применим соотношение (17) к (17) повторно, тогда получим
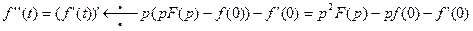 (21)
(21)
Применяя соотношение (17) к (21), получим
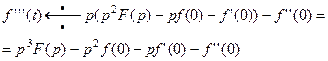
Продолжая этот процесс. получим

Замечание. Если функция  является оригиналом, то она является кусочно-непрерывной, т.е. может иметь на каждом отрезке при
является оригиналом, то она является кусочно-непрерывной, т.е. может иметь на каждом отрезке при 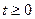 лишь конечное число точек разрыва первого рода. Если оригиналом является
лишь конечное число точек разрыва первого рода. Если оригиналом является 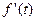 , то сама функция
, то сама функция  при всех
при всех 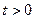 должна быть непрерывной. Если оригиналом является
должна быть непрерывной. Если оригиналом является 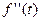 , то
, то 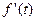 при всех
при всех 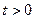 должна быть непрерывной и т.д.
должна быть непрерывной и т.д.
6. Теорема об интегрировании оригинала: интегрирование оригинала в пределах от 0 до  приводит к делению изображения на
приводит к делению изображения на  .Если
.Если 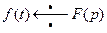 и
и  , то
, то 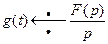 , т.е.
, т.е.
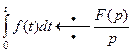 (22)
(22)
Доказательство. Обозначим 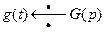 . Учитывая, что
. Учитывая, что 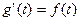 и
и 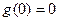 , получим в соответствии с теоремой дифференцирования оригинала
, получим в соответствии с теоремой дифференцирования оригинала
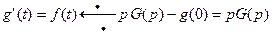 . Поскольку
. Поскольку  , то
, то 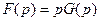 . Отсюда
. Отсюда 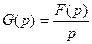 .
.
Из свойств (5) и (6) следует, что более сложным действиям над оригиналами (дифференцированию и интегрированию) соответствуют более простые действия над изображениями (умножение и деление на р).
7. Теорема о дифференцировании изображения: дифференцирование изображения сводится к умножению оригинала на  .
.
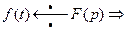 .
. 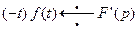 ,
,  ,
, 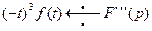 , ,
, ,
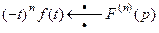 . (23)
. (23)
Доказательство. Учитывая, что  , найдем
, найдем 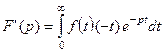 .
.
Следовательно,  . Применяя эту теорему несколько раз, последовательно найдем оригиналы для высших производных изображения.
. Применяя эту теорему несколько раз, последовательно найдем оригиналы для высших производных изображения.
8. Теорема об интегрировании изображения: если интеграл  сходится, то интегрирование изображения в пределах от
сходится, то интегрирование изображения в пределах от  до
до 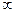 соответствует делению оригинала на
соответствует делению оригинала на  .
.
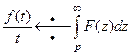 , (24)
, (24)
т.е. интегрирование изображения в пределах от  до
до 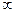 соответствует делению оригинала на
соответствует делению оригинала на  .
.
Пример 9. Найти изображение функции 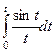 .
.
Учитывая, что 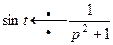 , получим по теореме об интегрировании изображения
, получим по теореме об интегрировании изображения 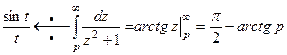 . Применяя теорему об интегрировании оригинала к полученному соотношению, найдем
. Применяя теорему об интегрировании оригинала к полученному соотношению, найдем 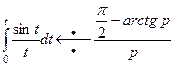 . Отметим, что интеграл
. Отметим, что интеграл 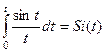 определяет неэлементарную функцию, которая называется интегральный синус.
определяет неэлементарную функцию, которая называется интегральный синус.
Пример 10. Найти изображение для функции  .
.
Учитывая, что 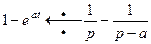 , с помощью теоремы об интегрировании изображения получим
, с помощью теоремы об интегрировании изображения получим 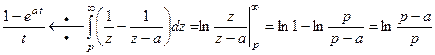 .
.
Следовательно,

Дата добавления: 2021-05-18; просмотров: 110; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
