Составляем канонические уравнения.

Выявляем степень статической неопределимости.

Л=3К - Ш = 3 -1 —2 = 1 (или Л = С_оп —3 = 4 —3= 1 ).

2. Выбираем основную систему и обращаем ее в нагруженную систему. Основ­ную систему получаем из заданной, устраняя нагрузку и горизонтальный опорный стержень левой опоры. Основная система, нагруженная заданной нагрузкой и горизонтальной неизвестной Х₁ возмещающей действие на раму устраненной связи.

3. Составляем каноническое уравнение:

Это уравнение в данном случае выражает условие равенства нулю горизонталь­ного перемещения точки А в системе совместного действия неиз­вестной Х₁ и заданной нагрузки.

4. Вычисляем перемещения  и  ; для этого предварительно строим эпюры 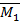и M_P .

а) Эпюра :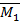

Нагрузим для этого основную систему только силой 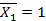 . Вертикальные опорные реакции от данного нагружения равны нулю (к та­кому заключению легко прийти, если составить уравнения

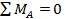   и 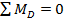. Горизонтальную реакцию найдем из уравнения :

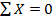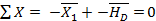, откуда

 

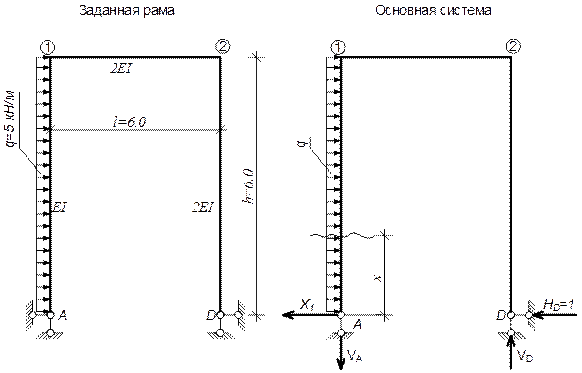
Изгибающие моменты в характерных сечениях элементов.

Элемент А1: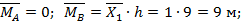

Элемент 12: ;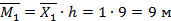  

Элемент CD: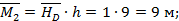

Б) Эпюра М _P

Нагрузив основную систему заданной нагрузкой, найдем сначала опорные реакции:

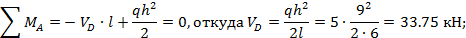
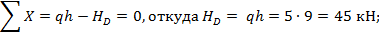
Теперь вычислим значения изгибающих моментов, необходимые для построе­ния эпюры М _P; эти же значения в дальнейшем используем при построении окон­чательной эпюры М:

Элемент A2: Здесь 0≤х ≤9м и 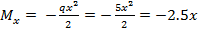 - уравнение квадратной параболы;

при х=0: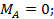

при x = 4,5 м: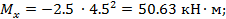

при х = 9м: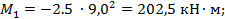

Элемент 1-2:

 

 

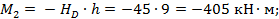
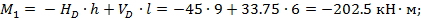
Элемент 2- D:

   

 

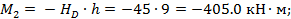
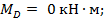
По данным построенных эпюр 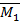и М _P находим:

Для получения  умножим площади ω, взятые из эпюры М _P на ординаты у, взятые из эпюры :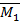

 

 

 

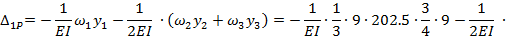
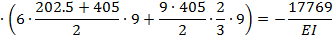
5. Находим из канонического уравнения значение Х₁:

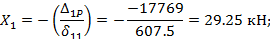
Знак плюс свидетельствует о правильности принятого направления найденной нами лишней неизвестной Х₁.

6. Строим окончательные эпюры Q, М и N.

 

а) Эпюра Q.

Вычислим опорные реакции, нагрузив основную систему заданной нагрузкой и известной теперь силой Х₁. Ввиду того что силы Х₁ и Н _D дей­ствуют по одной прямой, проходящей через центры опорных шарниров, относи­тельно которых следует составить уравнения моментов для определения реакций V_А и V _D и моментов относительно этих точек не дают, вертикальные опорные реак­ции в данном случае будут такими же, как и соответствующие реакции, вычис­ленные для построения эпюры М _P, т. е.

V_A = 33,75 кН; V_D = 33,75 кН.

Реакцию H_D найдем из уравнения ∑Х = 0:

—X₁ + qh — H_D = 0, откуда H_D = —X₁ + qh = — 29,25+5 · 9= 15,75 кН.

Вычисляем поперечные силы в характерных сечениях.

Элемент А1: 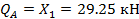 м;

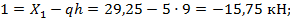
Элемент 1-2: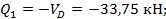  

Элементн 2 D:  

 

б) Эпюра М.

Произведем для характерных сечений сложение ординат эпюры М_P с соответ­ствующими ординатами эпюры 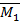 увеличенными в Х₁ = 29,25 раз.

Элемент А1: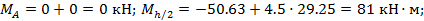  

 

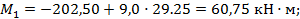
Найдем расстояние х₀ до сечения с максимальным изгибающим моментом, приравняв нулю поперечную силу в этом сечении:

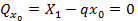, откуда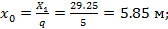

Тогда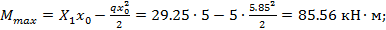

Элемент 1-2: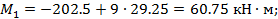  

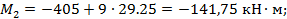
Элемент 2- D:  

 

в) Эпюра N.

Вычислим продольные силы в элементах рамы:

Элемент A1. Во всех сечениях рассматриваемого элемента продольная сила имеет постоянное значение: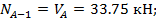

Элемент 1-2: В данном элементе продольная сила также постоянна:

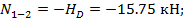
Элемент 2- D. И в данном элементе продольная сила постоянна:

 

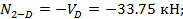
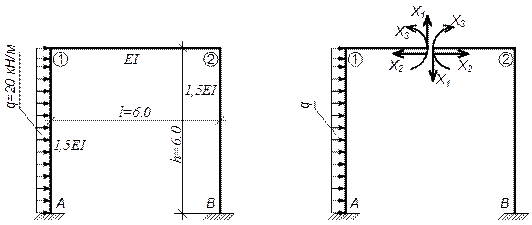
Пример 2. Построить эпюры Q , М и N для рамы. Жесткости элементов указаны на рисунке.

1. Устанавливаем степень статической неопределимости:

Л= 3К – Ш= 3·1 – 1=2 (или Л= С_оп -2=5-3 = 2) - рама дважды статически неопределима.

2. Выбираем основную систему и обращаем ее в нагруженную. Устранив заданную нагрузку, а также горизонтальный и вертикальный опорные стержни левой опоры (всю опору А), получим основную систему в виде ломаного бруса с одним свободным, другим защемленным концами. Основная система, нагружен­ная заданной нагрузкой и лишними неизвестными X₁ и Х₂, заменяющими соответ­ственно устраненные горизонтальный и вертикальный стержни опоры А.

Составляем канонические уравнения.

В данном случае будем иметь два канонических уравнения, что соответствует двум лишним неизвестным:

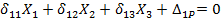
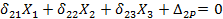
Первое из этих уравнений выражает условие равенства нулю горизонтального перемещения точки А в системе от совместного действия сил X₁ , Х₂ и заданной нагрузки, второе — условие равенства нулю вертикального перемеще­ния точки А от тех же сил.

4. Вычисляем перемещения , , 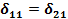, 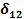∆_1Р и ∆_2Р; для этого предвари­тельно строим эпюры 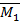и  от поочередного нагружения основной системы соот­ветственно силами ,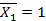

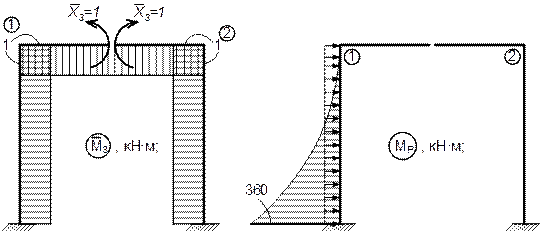
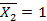 и эпюру М _P от нагружения основной системы заданной нагрузкой. Ввиду простоты построения указанных эпюр соответствую­щие вычисления здесь не приводим. Отметим только, что при определении момента в том или ином сечении следует рассматривать левую отсеченную часть рамы; в зтом случае не потребуется определять опорные реакции в заделке. Эпюры  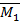, ,  и М _P показаны.

Теперь вычисляем перемещения, входящие в составленные выше каноничес­кие уравнения:

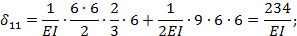
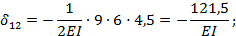
где 9·6 — площадь прямоугольной части эпюры 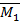 ; 4,5 — ордината, соответ­ствующая центру тяжести этой площади и взятая из эпюры

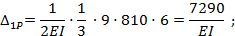
где  — площадь параболической части эпюры М _P; 6—ордината из эпюры 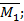 соответствующая центру тяжести указанной площади;

 

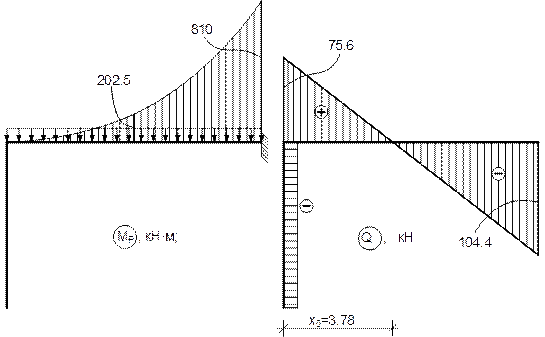
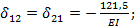 (на основании теоремы Максвелла);

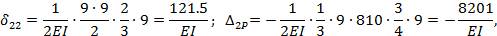
где 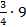 — ордината из зпюры , соответствующая центру тяжести площади пара­болической части эпюры М _P.

5. Подставляем найденные значения перемещений в канонические уравнения и решаем полученную систему уравнений:

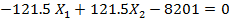
откуда Подставив найденное значение Х₁ в любое из уравнений, получим

Х₂ =75,6 кН.

Положительные значения Х₁ и Х₂ свидетельствуют о правильности выбора направлений обоих лишних неизвестных.

Проверим правильность решения системы канонических уравнений, подста­вив в каждое из них найденные значения Х₁ и Х₂:

234·8,1 — 121,5·75,6 + 7290 = 9185,4 — 9185,4 = 0;

— 121,5·8,1 + 121,5·75,6 — 8201 = — 9185,15 + 9185,4 = 0,25.

Погрешность во втором уравнении составляет всего (0,25/9185,15) 100 = 0,0027 %, поэтому практически в этом уравнении результат можно принять также равным нулю. Итак, система канонических уравнений решена правильно.

 

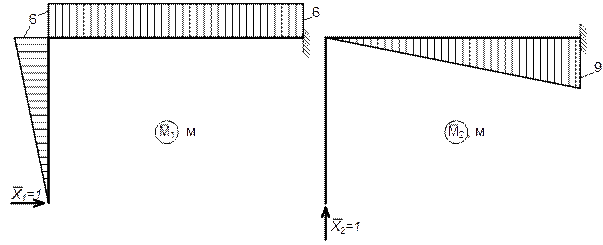
6. Строим окончательные эпюры Q, М и N.

а) Эпюра Q.

Вычислим значения поперечных сил для характерных сечений:

Элемент А-1: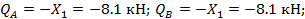

Элемент 1-С:

 

б) Суммарная (окончательная) эпюра М.

Сложим для характерных сечений системы ординаты эпюры М _P с соответствующими ординатами эпюры 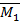 умноженными на Х₁ = 8,1 кН, и ор­динатами эпюры , умноженными на Х₂ = 75,6 кН.

Элемент А-1: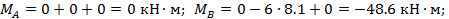

Элемент 1- C: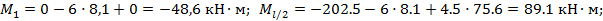

 

Найдем расстояние до сечения с максимальным изгибающим моментом, со­ставив выражение поперечной силы в этом сечении и приравняв его нулю:

 откуда

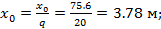
Тогда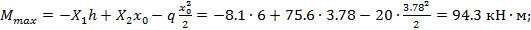

в) Эпюра N.

В каждом из элементов рамы продольная сила имеет свое постоянное значе­ние:

 

 

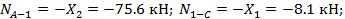
Пример 3. Построить эпюры Q , М и N для рамы. Жесткости элементов указаны на рисунке.

 

 

---

Дата добавления: 2021-05-18; просмотров: 69; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!