Хх.6 Свойства стрелки Пирса и штриха Шеффера
Основные свойства стрелки Пирса и штриха Шеффера приведены в таблице хх.6.
Таблица хх.6 Свойства функций «¯» и «/»
| N | Название | Формулировка |
| 1 | Определение функции «¯» | 
|
| 2 | Определение функции «/» |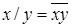 
|
| 3 | Коммутативности |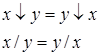 
|
| 4 | «Закон де Моргана» |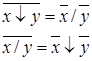 
|
| 5 | Соотношения для 
| 
|
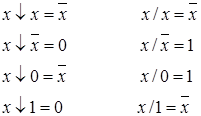
Следует отметить, что для обеих функций не справедливы законы ассоциативности и дистрибутивности.
Хх.7 Способы определения равносильности БФ
Существует три метода определения равносильности БФ:
– при помощь ТИ;
– при помощи законов алгебры логики;
– приведением к СДНФ или СКНФ.
Пусть даны три функции: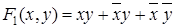 
;
;
.
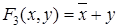Определим равносильность данных функций.
Хх.7.1 Определение равносильности БФ с помощью ТИ
Таблица хх.7 ТИ для определения равносильности F1, F2, F3
| x | y | 
| 
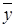
| xy | 
| 
| 
| 
| 
|
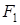
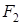
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если несколько функций принимают на всех наборах одни и те же значения, то эти функции равносильны. Получаем, что F1= F2= F3.
Хх.7.2 Определение равносильности БФ при помощи логических преобразований
.
.
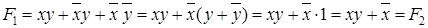Получили, что F1= F2= F3.
Доказательство равносильности нескольких функций данным методом является самым сложным и требует очень хорошего знания свойств и законов БФ.
|
|
|
Хх.7.3 Определение равносильности БФ при помощи СДНФ
Сразу можно сделать вывод, что F1 является СДНФ.
Любую БФ, равно как и ее ДНФ можно представить в виде СДНФ.
.
.
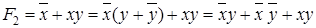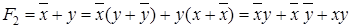Получаем, что F1= F2= F3.
Хх.8 Выражение одних БФ через другие
Логическим элементом (ЛЭ) будем называть вентиль, описываемый какой либо простой БФ. Логической схемой (цепью, структурой) будем называть совокупность ЛЭ, соединенных между собой так, что выполняется заданный закон функционирования.
Задача синтеза сложных логических схем эквивалентна представлению сложных логических функций простыми функциями, описывающими работу ЛЭ. Одна из проблем синтеза заключается в выборе типов ЛЭ, из которых должны собираться логические схемы. Набор элементов должен допускать построение любой сколь угодно сложной структуры, т.е. представлять функционально полную систему операций.
Однако ясно, что построение одной логической схемы из множества ЛЭ разных типов бывает нецелесообразно. В некоторых случаях гораздо эффективнее логическая структура, составленная из однотипных элементов.
БФ, при помощи которых можно выразить любую другую БФ носят название функционально полных. При проектировании их еще называют базисом.
|
|
|
Из определений бинарных функций (таких как «®», «Å», «/» и т.д.) можно заметить, что свойствами базиса обладают наборы «И – НЕ», «ИЛИ – НЕ», «И – ИЛИ – НЕ». Так мы их и будем называть: базис «И – НЕ», базис «ИЛИ – НЕ», базис «И – ИЛИ – НЕ». Но этими наборами не исчерпываются все возможные функционально полные системы. Существует также базис «¯», базис «/», базис «Å – И – 1» и другие.
Попытаемся выразить через стрелку Пирса и штрих Шеффера основные операции БА.
Дизъюнкция выражается следующим образом:
;
.
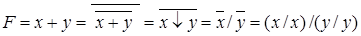Конъюнкция выражается как:
;
.
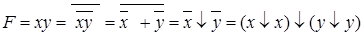Хх.9 Закон двойственности
Двойственной формой БФ называется такая форма, которая получается из заданной формы путем замены дизъюнкции на конъюнкцию и конъюнкции на дизъюнкцию. Двойственная форма функции F обозначается F*. Например, для булевой функции трех переменных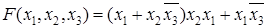 
двойственная форма запишется в виде 
.
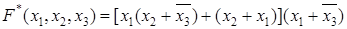Закон двойственности: если две БФ тождественны между собой, то и их двойственные формы тоже тождественны.
Следует заметить, что двойственную форму необходимо отличать от инверсной.
Дата добавления: 2021-05-18; просмотров: 183; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!