Хх.5 Свойства функции сложения по модулю два
Хх.1 Основные понятия и определения
Булева алгебра (БА) – раздел математической логики.
Основным понятием БА является высказывание (В). Под высказыванием понимают любое предложение, про которое можно однозначно сказать, истинно оно или ложно. Высказывания подразделяются на простые и сложные.
Под простым В понимают одно единственное предложение, про которое можно сказать истинно оно или ложно. Например: «Дважды два – пять», «Курица – не птица», «Путин – президент РФ».
Сложным В является предложение, состоящее из нескольких простых предложений (простых В), связанных между собой какими либо логическими связями. Под логическими связями понимаются грамматические союзы типа «НЕ», «И», «ИЛИ», «ЕСЛИ …, ТО …», и т.д.
Под булевой функцией (БФ) понимают сложное высказывание. Это такая функция, которая принимает лишь два значения (0 или 1). БФ всегда конечна и обозначается f, F. Простые высказывания, входящие в БФ, называются переменными или аргументами и обозначаются x, y, z, … В БА нет линейных коэффициентов, нет деления, корня, логарифма и т.д. В БА, как правило, используется двоичная арифметика, да и то не в полном объеме.
Есть два типа реализации БФ: положительная логика и отрицательная логика. В положительной логике 0 (ложь) соответствует низкому уровню сигнала, а 1 (истина) – высокому. Соответственно в отрицательной логике – наоборот.
|
|
|
БФ одной переменной называется симвилярной функцией. Существуют четыре симвилярные функции. Они приведены в таблице ХХ.1.
Таблица ХХ.1 Симвилярные БФ
| N | 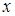
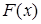
| 0 | 1 | Обозначение | Название |
| 0 | 
| 0 | 0 | 0 | Константа нуль |
| 1 | 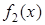
| 0 | 1 | 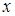
| Повторение |
| 2 | 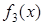
| 1 | 0 | 
| Отрицание (инверсия) |
| 3 | 
| 1 | 1 | 1 | Константа единица |
Хх.2 БФ двух переменных
БФ двух переменных называются бинарными.
Существует шестнадцать бинарных функций. Они приведены в таблице хх.2.
Таблица хх.2 БФ двух переменных
| x | y | F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
F0=0; F1=  ;
;
F2=  ; F3=
; F3=  ;
;
F4= 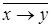 ; F5=
; F5= 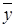 ;
;
F6= 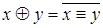 ; F7=
; F7= 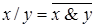 ;
;
F8=  ; F9=
; F9= 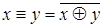 ;
;
F10= 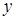 ; F11=
; F11=  ;
;
F12= 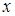 ; F13=
; F13= 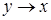 ;
;
F14= 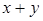 ; F15=1.
; F15=1.
Из всех возможных бинарных БФ выделяются нижеследующие основные.
Константа 0 – F0.
Константа 1 – F15.
|
|
|
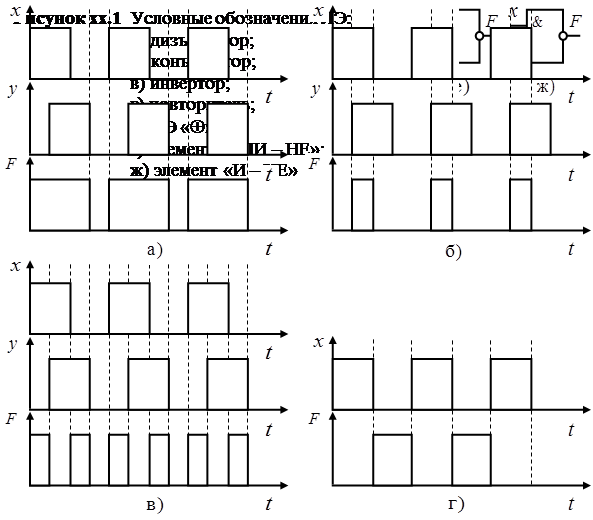
Дизъюнкция (функция «ИЛИ», операция «ИЛИ», «ИЛИ», включающее «ИЛИ», соединение, логическое сложение) – БФ, таблица истинности (ТИ) которой соответствует F14 в таблице хх.2. Обозначается с помощью знака «+» или «Ú», например F=x+y (F=xÚy). Условное обозначение логического элемента (ЛЭ), реализующего дизъюнкцию (дизъюнктора), изображено на рисунке хх.1.а, а его временные диаграммы на рисунке хх.2.а.
Конъюнкция (функция «И», операция «И», «И», логическое умножение) – БФ, ТИ которой соответствует F8 в таблице хх.2. Обозначается так же, как произведение в обычной алгебре или с помощью знака «&» («Ù»), например F=x&y (F=xy). Условное обозначение ЛЭ, реализующего конъюнкцию (конъюнктора), изображено на рисунке хх.1.б, а его временные диаграммы на рисунке хх.2.б.

 |
Отрицание (инверсия) и повторение – БФ, ТИ которых были приведены в таблице хх.1. Отрицание обозначается чертой, которая ставится над переменной. Например, отрицание переменной х, читаемое «НЕ х», записывается в виде
 . Условное обозначение ЛЭ, реализующего отрицание (инвертора), изображено на рисунке хх.1.в, а его временные диаграммы на рисунке хх.2.г. Условное обозначение ЛЭ, реализующего повторение (повторителя), изображено на рисунке хх.1.г.
. Условное обозначение ЛЭ, реализующего отрицание (инвертора), изображено на рисунке хх.1.в, а его временные диаграммы на рисунке хх.2.г. Условное обозначение ЛЭ, реализующего повторение (повторителя), изображено на рисунке хх.1.г. |
|
|
Сложение по модулю два (исключающее «ИЛИ») – БФ, ТИ которой соответствует F6 в таблице хх.2. Обозначается с помощью знака «Å», например F=xÅy. Условное обозначение ЛЭ, реализующего сложение по модулю два, изображено на рисунке хх.1.д, а его временные диаграммы на рисунке хх.2.в.
Стрелка Пирса (функция «ИЛИ – НЕ») – БФ, ТИ которой соответствует F1 в таблице хх.2. Обозначается с помощью знака «¯». Условное обозначение ЛЭ, изображено на рисунке хх.1.е.
Штрих Шеффера (функция «И – НЕ») – БФ, ТИ которой соответствует F7 в таблице хх.2. Обозначается с помощью знака «/». Условное обозначение ЛЭ, изображено на рисунке хх.1.ж.
Равнозначность (эквивалентность) – БФ, ТИ которой соответствует F9 в таблице хх.2. Обозначается с помощью знака «º» или «~».
Импликация от х к у – БФ, ТИ которой соответствует F11 в таблице хх.2. Обозначается с помощью знака «®».
Хх.3 Понятие о СДНФ и СКНФ
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Под элементарной конъюнкцией понимаются конъюнкции одной, двух, трех и т.д. переменных с отрицанием или без.
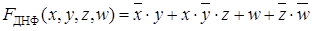 .
.
ДНФ заданной БФ можно записать несколькими способами, причем одна запись будет отличаться от другой.
|
|
|
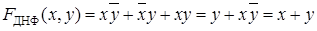 .
.
Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций.
 .
.
Совершенной ДНФ (КНФ) называется такая ДНФ (КНФ), в состав каждой элементарной конъюнкции (дизъюнкции) которой входят все переменные, входящие в БФ.
Для нахождения СДНФ и СКНФ любой БФ существуют следующие алгоритмы.
Пусть БФ трех переменных F задана таблицей истинности (таблица хх.3).
Таблица хх.3 ТИ для F.
| x | y | z | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Составим СДНФ для F:
– выделяем наборы переменных, на которых функция равна 1;
– записываем для этих наборов конъюнкции, при этом если переменная равна 1, то эта переменная записывается без отрицания, если же переменная равна 0, то такая переменная записывается с отрицанием;
– объединяем элементарные конъюнкции знаками дизъюнкций;
– полученное выражение будет являться совершенной ДНФ.
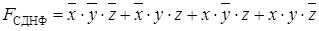 .
.
Алгоритм нахождения СКНФ:
– выделяем те наборы переменных, на которых функция равна 0;
– из этих наборов переменных составляем дизъюнкции, учитывая то, что если переменная равна 0, то она записывается без отрицания, а если 1 – с отрицанием;
– объединяем элементарные дизъюнкции знаками конъюнкций;
– полученное выражение является совершенной КНФ.
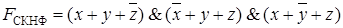 .
.
Рангом функции называется наибольшее число переменных, входящих в ДНФ.
Длиной функции называется число элементарных конъюнкций (дизъюнкций) входящих в эту функцию.
Универсальными БФ называются такие БФ, при помощи которых можно описать (представить) любое логическое выражение.
Кратчайшей называется функция, имеющая наименьший ранг и наименьшую длину.
Хх.4 Основные законы (аксиомы) БА
Булеву алгебру можно применять, зная три основные операции: «И», «ИЛИ», «НЕ». Однако полезно знать некоторые основные тождества (тавтологии), приведенные в таблице хх.4.
Таблица хх.4 Основные тождества БА
| N | Название | Формулировка |
| 1 | Коммутативности (переместительный) | 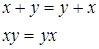
|
| 2 | Ассоциативности (сочетательный) | 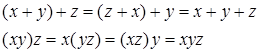
|
| 3 | Дистрибутивности | 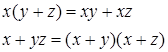
|
| 4 | Соотношения абсорбции | 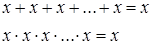
|
| 5 | Теорема де Моргана | 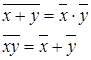
|
| 6 | Двойного отрицания | 
|
| 7 | Двойственности | 
|
| 8 | Пустого множества | 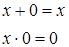
|
| 9 | Универсального множества | 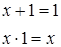
|
| 10 | Склеивания | 
|
| 11 | Поглощения | 
|
| 12 | Следствие из 3 | 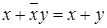
|
| 13 | Обобщенный закон Клода- Шеннона | 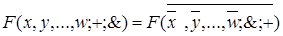
|
Хх.5 Свойства функции сложения по модулю два
В таблице хх.5 приведены основные свойства функции сложения по модулю два.
Таблица хх.5 Свойства функции «Å»
| N | Название | Формулировка |
| 1 | Определение операции | 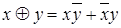
|
| 2 | Коммутативности | 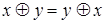
|
| 3 | Ассоциативности | 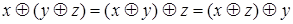
|
| 4 | Дистрибутивности | 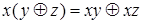
|
| 5 | «Закон де Моргана» | 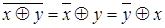
|
| 6 | Соотношения для 
| 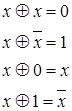
|
Дата добавления: 2021-05-18; просмотров: 220; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
