Производные тригонометрических функций
Министерство образования и науки Республики Казахстан
ВОСТОЧНО КАЗАХСТАНСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА ИМЕНИ С.АМАНЖОЛОВА
ВЫСШИЙ КОЛЛЕДЖ
Дисциплина: «Основы высшей математики»
Специальность: «Информационные системы» ИС 1-Б
Подготовила Курманова А.Б.
Лекция 03.04.20 г.
Тема: Правила дифференцирования и производные элементарных функции
- Постоянный множитель c можно выносить за знак производной:
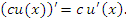
Правило 1 непосредственно вытекает из определения производной функции и свойства пределов функций, согласно которому постоянный множитель можно выносить за знак предела.
- Если существуют производные
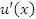 и
и 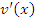 , то производная от суммы (разности) функций
, то производная от суммы (разности) функций  и
и 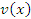 равна сумме (разности) производных:
равна сумме (разности) производных:
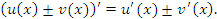
Правило дифференцирования суммы или разности функций также следует из определения производной функции и свойства пределов функций, согласно которому предел суммы (или разности) функций равен сумме (или разности) соответствующих пределов.
- Если существуют производные
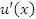 и
и 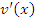 , то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
, то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
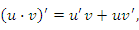

Правила дифференцирования функций
Правило 3. Если существуют производные 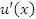 и и 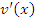 , то выполняется следующее правило дифференцирования произведения функций: , то выполняется следующее правило дифференцирования произведения функций:
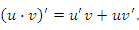 Доказательство. По определению производной
Доказательство. По определению производной
 Преобразуем выражение в числителе, вычитая и прибавляя произведение
Преобразуем выражение в числителе, вычитая и прибавляя произведение 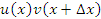 ; затем сгруппируем слагаемые: ; затем сгруппируем слагаемые:
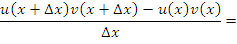 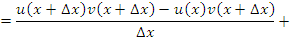 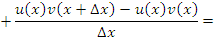  Выполняя предельный переход и учитывая, что
Выполняя предельный переход и учитывая, что
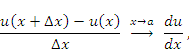  получим требуемое утверждение.
получим требуемое утверждение.
|
|
|
|
***
Правило 4. Если существуют производные 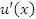 и и 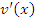 , то выполняется следующее правило дифференцирования частного от деления функций: , то выполняется следующее правило дифференцирования частного от деления функций:
 Доказательство этого правила по своей сути не отличается от предыдущего:
Доказательство этого правила по своей сути не отличается от предыдущего:
 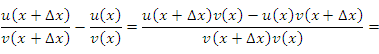 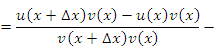 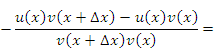 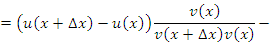 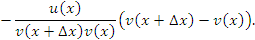 Учитывая свойства пределов функций, получим требуемый результат:
Учитывая свойства пределов функций, получим требуемый результат:
 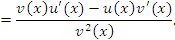
|
Дифференцирование параметрический заданных функций (пример)
Пусть функция 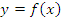 задана параметрическими уравнениями
задана параметрическими уравнениями

где t – параметр.
Тогда производная этой функции по переменной x равна отношению производных 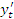 и
и  по параметру t:
по параметру t:
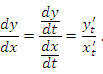
Пример 1. Найти производную функции 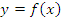 , заданной уравнениями в параметрической форме:
, заданной уравнениями в параметрической форме:
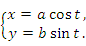
Решение. Очевидно, что

Следовательно,

Производная степенной, логарифмической и показательной функций
Пусть n – произвольное вещественное число. Тогда

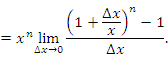
Используя соотношение эквивалентности
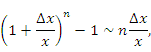
получим, что
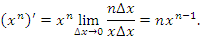
Пусть 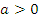 и
и  . Тогда
. Тогда


Используя соотношение эквивалентности
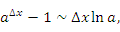
получим правило дифференцирования показательной функции:
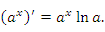
Эта формула принимает особенно простой вид, если основанием является число e:
|
|
|

Функция 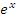 является уникальной, ибо это единственная функция, производная от которой совпадает с самой функцией.
является уникальной, ибо это единственная функция, производная от которой совпадает с самой функцией.
Покажем, что для любого x > 0 выполняется следующее правило дифференцирования логарифмической функции:
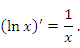
Действительно, приращение этой функции можно представить в виде
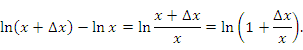
Если ∆x → 0, то бесконечно малая в правой части этого равенства удовлетворяет соотношению эквивалентности
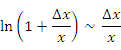
и, следовательно,
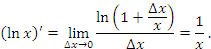
Примеры:

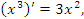

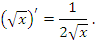
Производные тригонометрических функций
- По определению производной функции

Учитывая тригонометрическое тождество

и первый замечательный предел, получим

- Вывод правила дифференцирования функции
 основывается на тригонометрическом тождестве
основывается на тригонометрическом тождестве
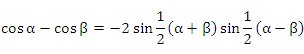
и первом замечательном пределе:
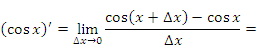
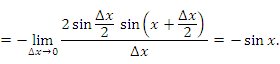
- Для вывода правила дифференцирования функции
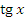 представим эту функцию в виде отношения синуса к косинусу и воспользуемся правилом дифференцирования частного от деления двух функций:
представим эту функцию в виде отношения синуса к косинусу и воспользуемся правилом дифференцирования частного от деления двух функций:
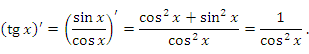
- Аналогично обосновывается правило дифференцирования функции
 :
:
Дата добавления: 2021-04-23; просмотров: 90; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
