Решение задач на выполнение теоретико-множественных операций и на подсчет количества элементов множеств.
Повторить теорию из 1 части.
2. Выполнить практическую 1 и результаты выслать мне по эл. почте.
I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.
Раздел 1. Элементы т еории множеств.
1. Понятие множества. Пустое множество. Подмножество.
2. Какими способами можно задать множество?
3. Конечное множество. Изображение множеств кругами Эйлера.
4. Как различаются множества по числу элементов?
5. Какое свойство называется характеристическим свойством?
6. Что называется объединением множеств А и В?
7. Что называется пересечением множеств А и В?
8. Разность множеств. Симметрическая разность множеств.
9. Дополнение к множеству.
10. Соответствие между множествами.
11. Взаимно-однозначное соответствие.
12. Декартово произведение множеств.
13. Декартова степень множества.
14. Мощность конечного множества.
Раздел 2. Элементы алгебры высказывания.
1. Предмет математической логики.
2. Понятие высказывания.
3. Понятие сложного высказывания.
4. Логические операции над высказываниями, примеры.
5. Перечислить логические операции.
6. Таблица истинности для формул алгебры высказываний и методика её построения.
7. Дизъюнкция двух высказываний.
8. Конъюнкция двух высказываний.
9. Импликация двух высказываний.
10. Эквиваленция двух высказываний.
11. Операция двоичного сложения двух высказываний.
12. Отрицание высказывания.
13. Смысл инверсии.
14. Определение формулы. Истинностные значения формул. Определение функции. Представления истинностных функций формулами.
|
|
|
15. Определения тавтологии и противоречия. Закон контрапозиции, исключенного третьего, двойного отрицания.
16. Равносильность. Равносильные преобразования формул. Связь равносильности с тавтологиями.
17. Определения ДН-формы и КН-формы, приводимость всякой формулы к нормальной форме, примеры.
18. Логическое следствие
19. Закон двойственности.
Раздел 3. Булевы функции.
1. Булева функция.
2. Способы задания булевых функций.
3. Равносильные булевы функции.
4. Операция двоичного сложения.
5. Совершенная дизъюнктивная нормальная форма и методика ее построения. Определения СДН-формы и СКН-формы, алгоритм нахождения.
6. Что понимается под минимизацией логических функций?
7. Перечислить методы минимизации логических функций
8. Полином Жегалкина (общая формула).
9. Функция, сохраняющая константу 0 (определение).
10. Функция, сохраняющая константу 1 (определение).
11. Самодвойственная функция (определение).
12. Линейная функция.
13. Монотонная функция .
14. Теорема Поста (критерий функциональной полноты системы функций).
15. Понятие логического элемента компьютера.
Раздел 4. Основы алгебры предикатов.
|
|
|
1. Что называется предикатом?
2. Что называется областью истинности предиката?
3. Что называется конъюнкцией предиката?
4. Что называется отрицанием предиката? Приведите примеры предикатов.
5. Понятие квантора существования.
6. Понятие квантора общности.
7. Область действия квантора (определение).
Раздел 5. Основы теории алгоритмов.
1. Понятие алгоритма.
2. Основные свойства алгоритмов.
3. Исполнитель алгоритма и его характеристики.
4. Алгоритмизация.
II. ПРАКТИЧЕСКАЯ ЧАСТЬ.
Раздел 1. Элементы т еории множеств.
Решение задач на определение видов множеств, вычисление количества подмножеств конечных множеств, отыскание элементов множеств.
1.Запишите множество всех натуральных делителей числа 21, определите его вид и найдите мощность.
2. Заданы множества A=  и B=
и B=  .
.
а) Является ли одно из них подмножеством другого?
б) Найдите мощности множеств А и В.
в) Определите количество подмножеств множества А.
3. Найдите множество В, заданное характеристическим свойством
 .
.
4. Укажите множество действительных чисел, соответствующее записи
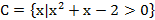 .
.
5. Найдите множество A, заданное характеристическим свойством
 .
.
6. Для множества  .
.
|
|
|
а)Вычислить количество всех подмножеств.
б ) Найти их.
в) Вычислить их мощность.
Решение задач на выполнение теоретико-множественных операций и на подсчет количества элементов множеств.
1. Даны числовые промежутки 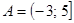 ,
, 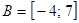 и
и 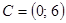 . Найдите множества и изобразите с помощью кругов Эйлера:
. Найдите множества и изобразите с помощью кругов Эйлера:
а)  ; б)
; б) 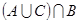 ; в)
; в)  ; г)
; г)  .
.
2. Результаты статистических исследований занесены в таблицу:
| Социологические группы | Одобряют безоговорочно | Одобряют с некоторыми сомнениями | Сомневаются | Негативная реакция |
| Мужчины - преподаватели | 3 | 4 | 5 | 10 |
| Женщины - преподаватели | 8 | 9 | 7 | 11 |
| Юноши - студенты | 5 | 4 | 4 | 9 |
| Девушки - студенты | 6 | 6 | 8 | 9 |
Обозначим М – множество опрошенных лиц мужского пола, С – сомневающиеся, П – множество преподавателей, О множество тех, кто одобряет. Изобразите множества кругами Эйлера и найдите число их элементов:
а)  ; б)
; б)  .
.
3. Выполните действие  и определите мощность полученного множества.
и определите мощность полученного множества.
4.Найдите декартово произведение множеств А и В: А=(-1,0,1,2), В=(-2,0,2)
5. Решить задачу, используя круги Эйлера. Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?
|
|
|
Дата добавления: 2021-04-15; просмотров: 423; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
