Геометрические приложения кратных интегралов
Тема 4.5. Интегральное исчисление функций
Нескольких переменных
Двойные интегралы
Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой f( x, y) = 0.
y
0 x
Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью D. Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область D.
С геометрической точки зрения D - площадь фигуры, ограниченной контуром.
Разобьем область D на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние Dх i, а по оси у – на Dу i. Вообще говоря, такой порядок разбиения необязателен, возможно разбиение области на частичные участки произвольной формы и размера.
Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны Si = D xi × D yi .
В каждой частичной области возьмем произвольную точку Р(х i, yi) и составим интегральную сумму
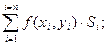
где f – функция непрерывная и однозначная для всех точек области D.
Если бесконечно увеличивать количество частичных областей Di, тогда, очевидно, площадь каждого частичного участка Si стремится к нулю.
Если при стремлении к нулю шага разбиения области D интегральные суммы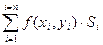 
имеют конечный предел, то этот предел называется двойным интегралом от функции f( x, y) по области D.
|
|
|
С учетом того, что Si = D xi × D yi получаем:
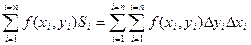
В приведенной выше записи имеются два знака S, т.к. суммирование производится по двум переменным х и у.
Т.к. деление области интегрирования произвольно, также произволен и выбор точек Р i, то, считая все площади Si одинаковыми, получаем формулу:
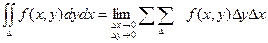
Условия существования двойного интеграла
Сформулируем достаточные условия существования двойного интеграла.
Теорема. Если функция f( x, y) непрерывна в замкнутой области D, то двойной интеграл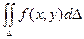 
существует.
Теорема. Если функция f( x, y) ограничена в замкнутой области D и непрерывна в ней всюду, кроме конечного числа кусочно – гладких линий, то двойной интеграл 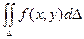существует.
Свойства двойного интеграла
1) 
2) 
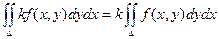
3) Если D = D1 + D2, то
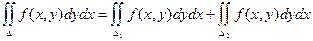
4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.
5) Если f(x, y) ³ 0 в области D, то 
.
6) Если f1(x, y) £ f2(x, y), то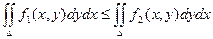 
.
7) 
.
Вычисление двойного интеграла
Теорема. Если функция f( x, y) непрерывна в замкнутой области D, ограниченной линиями х = a, x = b, ( a < b), y = j( x), y = y( x), где j и y - непрерывные функции и j £ y, тогда
|
|
|
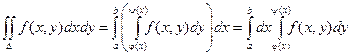
y y = y( x)
 |
D
y = j( x)
a b x
Пример. Вычислить интеграл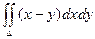 
, если область D ограничена линиями: y = 0, y = x2, x = 2.
y
4
D
0 2 x
= 
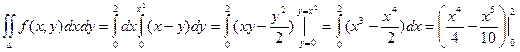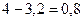
Теорема. Если функция f( x, y) непрерывна в замкнутой области D, ограниченной линиями y = c, y = d ( c < d), x = F( y), x = Y( y) ( F( y) £ Y( y)), то
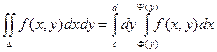
Пример. Вычислить интеграл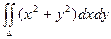 
, если область D ограничена линиями
y = x, x = 0, y = 1, y = 2.
y
 |
y = x
2
|
|
|
D
1
0 x
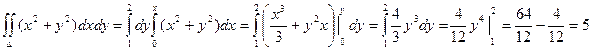
Пример. Вычислить интеграл 
, если область интегрирования D ограничена линиями х = 0, х = у2, у = 2.
= 
= 
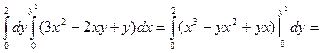
Геометрические приложения кратных интегралов
Дата добавления: 2021-04-15; просмотров: 75; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!