Найти значения величин используемых ресурсов (х,у), при которых фирма-производитель получит максимальную прибыль, если заданы производственная функция
Функции нескольких переменных
Найти область определения функции 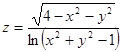 .
.
Решение. Область определения представляет собой решение системы неравенств:
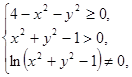
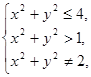

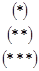
Множество значений х, у, удовлетворяющих (*), представляет собой внутренность круга с центром (0; 0) и радиусом, равным 2. Решения (**) – внешность круга радиуса 1 с центром (0; 0). Условие (***) означает, что в область определения не входит окружность с центром в начале координат и радиусом, равным 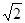 . Таким образом, область определения представляет собой два кольца (см. рис. 15.1).
. Таким образом, область определения представляет собой два кольца (см. рис. 15.1).
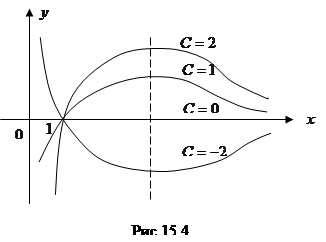 Построить линии уровня функции
Построить линии уровня функции 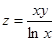 .
.
Решение. Линии уровня имеют вид 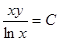 , т.е. представляют собой график функции
, т.е. представляют собой график функции 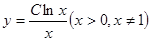 . Функция определена при
. Функция определена при  , имеет правостороннюю асимптоту, ось абсцисс, вертикальную асимптоту – ось ординат. Единственная критическая точка
, имеет правостороннюю асимптоту, ось абсцисс, вертикальную асимптоту – ось ординат. Единственная критическая точка  - это точка максимума. Значение функции при этом
- это точка максимума. Значение функции при этом 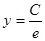 . Таким образом, линии уровня имеют вид, показанный на рис. 15.4.
. Таким образом, линии уровня имеют вид, показанный на рис. 15.4.
Найти предел 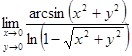
Решение. Обозначим 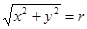 . Тогда условие
. Тогда условие  равносильно тому, что
равносильно тому, что 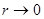 и искомый предел примет вид:
и искомый предел примет вид:
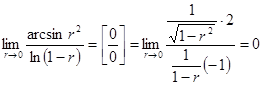 (применили правило Лопиталя).
(применили правило Лопиталя).
Исследовать на непрерывность в точке (0;0) функцию 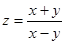 .
.
Решение. Будем приближаться к точке (0;0) по направлению прямых 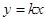 . Тогда будем иметь
. Тогда будем иметь 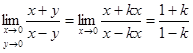 .
.
Значения пределов различны при различных 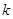 , следовательно, предела функции двух переменных не существует, и функция не является непрерывной в точке (0;0).
, следовательно, предела функции двух переменных не существует, и функция не является непрерывной в точке (0;0).
|
|
|
Задания по теме 1.
Найти области определения функций:
1. 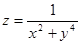 4.
4. 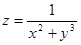 7.
7. 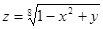
2. 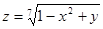 5.
5. 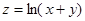 8.
8. 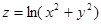
3. 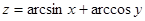 6.
6. 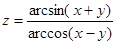 .7.
.7. 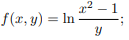
8. 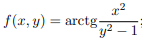 9.
9. 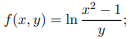 10.
10. 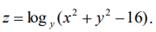
Найти линии уровня функции в явном виде y = g(x,C):
11. 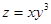 12.
12. 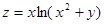 13.
13. 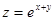
14. 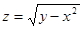 15.
15. 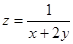 16.
16. 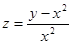
17. 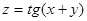 18.
18. 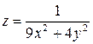 19.
19. 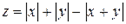 20.
20. 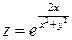
Найти пределы:
21.
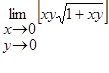
| 22. 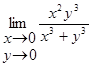
| 23. 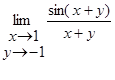
|
24.
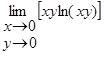 27.
27. 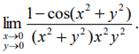
| 25. 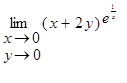 28.
28. 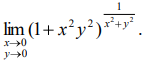
| 26. 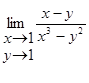 29.
29. 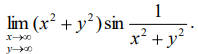
|
30. 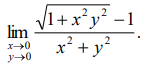
|
2. Частные производные, градиент, дифференциал
Найти частные производные функции 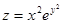 .
.
Решение. При дифференцировании по 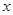 считаем постоянной величину
считаем постоянной величину  .Таким образом,
.Таким образом, 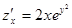 . При дифференцировании по
. При дифференцировании по  считаем постоянной величину
считаем постоянной величину 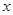 , следовательно,
, следовательно, 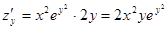 .
.
Найти частные производные второго порядка функции двух переменных 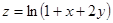 .
.
Решение. Частные производные 1 – го порядка имеют вид:
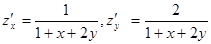 .
.
Считая их новыми функциями двух переменных, найдем их частные производные. Получаем:
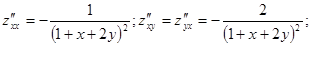
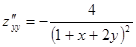 .
.
Найти длину вектора 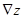 градиента функции
градиента функции 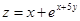 в точке (0;0).
в точке (0;0).
|
|
|
Решение. Компонентами вектора 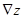 (15.7) являются частные производные функции, т.е.
(15.7) являются частные производные функции, т.е. 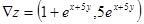 . В точке (0;0) получаем
. В точке (0;0) получаем 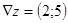 . Соответственно длина вектора
. Соответственно длина вектора 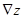 равна
равна 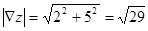 .
.
Найти производную функции 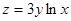 в точке (2;0) по направлению, параллельному биссектрисе первого координатного угла.
в точке (2;0) по направлению, параллельному биссектрисе первого координатного угла.
Решение. Прямая, проходящая через точку (2,0) параллельно биссектрисе первого координатного угла, задается уравнением 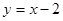 (см. (4.7)). Ее углы с осями координат (как и у биссектрисы) равны
(см. (4.7)). Ее углы с осями координат (как и у биссектрисы) равны 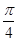 . Следовательно. По формуле (15.6):
. Следовательно. По формуле (15.6):
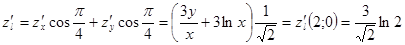 .
.
Задания по теме 2
Найти частные производные функций:
1. 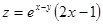 . .
| 2. 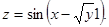
| 3. 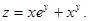
|
4. 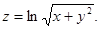
| 5. 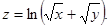
| 6. 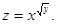
|
7. 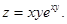 10.
10. 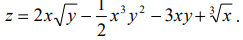
| 8. 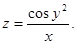
| 9. 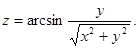
|
Найти полные дифференциалы функций:
11. 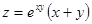 . 12.
. 12. 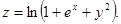 13.
13. 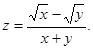
14. 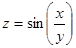 . 15.
. 15. 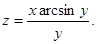 16.
16. 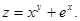
17. 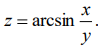 18.
18. 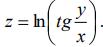 19.
19. 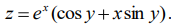
20. 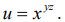
Найти производные функций по заданным направлениям l:
21. 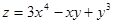 ; l составляет с осью Ох угол
; l составляет с осью Ох угол 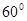 .
.
22. 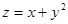 ; l – биссектриса 1-го координатного угла.
; l – биссектриса 1-го координатного угла.
23. Вычислить производную функции 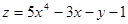 в точке М(2;1)
в точке М(2;1)
по направлению l – прямой МN, где N (5,5).
24. Вычислить производную функции 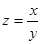 в точке М(1;1) по направлению l – перпендикуляра к прямой y = 2х – 1.
в точке М(1;1) по направлению l – перпендикуляра к прямой y = 2х – 1.
25. Найти производную функции z =arctg(xy) в точке (1;1) в направлении биссектрисы первого координатного угла
|
|
|
26. Найти производную функции z= 3x4 -xy+y3 в точке (1;2) в направлении, составляющем с осью Ox угол 60˚.
27. Найти производную функции u =xyz в точке (5,1,2) в направлении, идущем от этой точки к точке (9,4,14).
28. Найти производную функции ln( ) 2 2 z x y в точке (3,4) в направлении градиента функции
29. Найти точки, в которых производные функции z= x2-2xy+ y2 по любому направлению равны нулю.
Найти градиент функции z = f(x,y) и его модуль для функций в указанных точках М:
30. 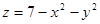 ; М(1;2). 32.
; М(1;2). 32. 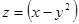 ; М(0;3).
; М(0;3).
31. 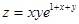 ; М(0;-1). 33.
; М(0;-1). 33. 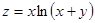 ; М(-1;2).
; М(-1;2).
34. 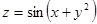 ; М
; М 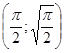 . 35
. 35 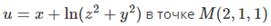
36 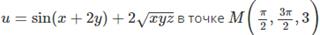 37
37 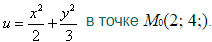
38  39 z=7-5x2-10y2 в точке M(-5;7)
39 z=7-5x2-10y2 в точке M(-5;7)
40 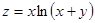 ; М(-1;2).
; М(-1;2).
3. Экстремум функции нескольких переменных. Условный экстремум
Краткая теория.
1. Точка 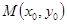 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции 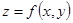 если существует окрестность точки М, такая, что для всех точек
если существует окрестность точки М, такая, что для всех точек 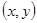 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство
 .
.
2.Если в точке максимума или минимума обе частные производные существуют и непрерывны, то они равны нулю в этой точке (необходимое условие экстремума).
3.Если в точке 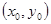 обе частные производные обращаются в нуль, то характер этой точки определяется величиной
обе частные производные обращаются в нуль, то характер этой точки определяется величиной 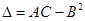 , где
, где 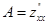 ,
, 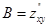 ,
, 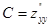 .
.
При 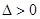 имеется экстремум (максимум при
имеется экстремум (максимум при 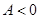 и минимум при
и минимум при 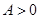 ).
).
|
|
|
При 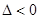 функция в данной точке не имеет экстремума.
функция в данной точке не имеет экстремума.
При 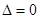 вопрос о наличии экстремума остается открытым (достаточное условие экстремума).
вопрос о наличии экстремума остается открытым (достаточное условие экстремума).
4.Наибольшее (наименьшее) значение функции (глобальный максимум (минимум)) 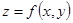 определяется как наибольшее (наименьшее) значение функции в замкнутой области из ее значений в критических точках внутри области и на ее границе.
определяется как наибольшее (наименьшее) значение функции в замкнутой области из ее значений в критических точках внутри области и на ее границе.
5. Точка 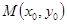 называется точкой условного максимума (минимума) функции
называется точкой условного максимума (минимума) функции 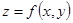 при условии
при условии 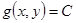 если, существует такая окрестность этой точки, что во всех точках (х, у) из этой окрестности, удовлетворяющих условию g(x, у) = С, выполняется неравенство
если, существует такая окрестность этой точки, что во всех точках (х, у) из этой окрестности, удовлетворяющих условию g(x, у) = С, выполняется неравенство  .
.
Уравнение 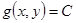 называется уравнением связи. Точка условного экстремума является точкой экстремума функции
называется уравнением связи. Точка условного экстремума является точкой экстремума функции 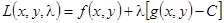 . Функция L называется функцией Лагранжа, а
. Функция L называется функцией Лагранжа, а 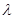 , – множителем Лагранжа.
, – множителем Лагранжа. 
6.При исследовании функции на экстремум рекомендуется пользоваться следующей схемой:
1. Найти частные производные 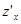 и
и 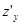
2. Решить систему уравнений 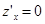 и
и 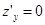 и найти критические точки функции.
и найти критические точки функции.
3. Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
4. Найти экстремумы (экстремальные значения) функции.
Найти экстремумы функции 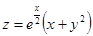 .
.
Решение.
1. Находим частные производные:
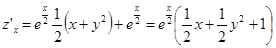 ;
; 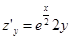 .
.
2. Находим критические точки функции из системы
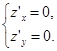
Получаем 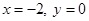 , т.е.
, т.е. 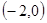 – единственная критическая точка.
– единственная критическая точка.
3. Находим частные производные второго порядка:
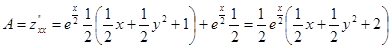 ;
;
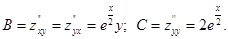
Имеем 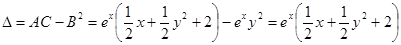 .
.
В точке (–2; 0) имеем 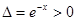 ,
, 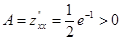 . Таким образом, (– 2; 0) – точка минимума.
. Таким образом, (– 2; 0) – точка минимума.
4. Находим минимум функции 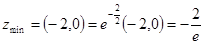 .
.
Найти экстремумы функции 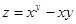 .
.
Решение. 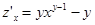 ;
; 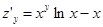 . Легко проверить, что равенство
. Легко проверить, что равенство 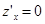 выполняется в трех случаях: при х = 1, при у = 0ипри
выполняется в трех случаях: при х = 1, при у = 0ипри 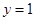 . В первых двух случаях уравнение
. В первых двух случаях уравнение 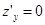 не имеет решений, так что единственное решение системы
не имеет решений, так что единственное решение системы
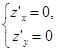
есть 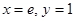 , т.е.критическая точка (е; 1) – единственная. Имеем
, т.е.критическая точка (е; 1) – единственная. Имеем
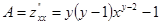 ;
; 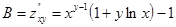 ;
; 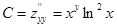 .
.
В точке 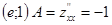 ;
; 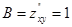 ;
; 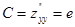 .
.
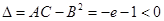 , так что функция экстремумов не имеет. Такая точка (е; 1) есть седловая точка.
, так что функция экстремумов не имеет. Такая точка (е; 1) есть седловая точка.
Найти экстремумы функции 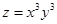 .
.
Решение. 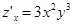 ;
; 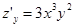 . Очевидно, (0; 0) – единственная критическая точка:
. Очевидно, (0; 0) – единственная критическая точка: 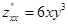 ;
; 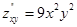 ;
; 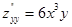 . Очевидно, в точке (0; 0)
. Очевидно, в точке (0; 0) 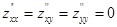 , т.е.
, т.е. 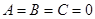 ,
, 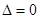 , и вопрос об экстремуме остается открытым, так что требуется дополнительное исследование.
, и вопрос об экстремуме остается открытым, так что требуется дополнительное исследование.
Очевидно, в любой окрестности точки (0; 0) функция может принимать и положительные, и отрицательные значения (например, в точке (1; 1) z = 1 > 0, а в точке
(– 1; 1) z = – 1 < 0); в самой же точке (0; 0) функция равна нулю. Таким образом, ни в какой своей окрестности точка (0; 0) не является ни точкой максимального, ни точкой минимального значения, т.е. функция экстремумов не имеет.
Найти наибольшее и наименьшее значение функции 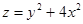 на круге
на круге 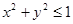 .
.
Решение. Критическая точка 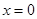 ,
, 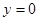 – единственная и расположена внутри круга
– единственная и расположена внутри круга 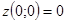 . На границе круга
. На границе круга 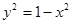 и
и 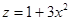 ,где
,где 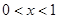 . Таким образом, на границе имеем
. Таким образом, на границе имеем 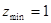 ,
, 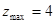 . Следовательно, наименьшее значение
. Следовательно, наименьшее значение 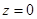 принимается внутри круга, наибольшее
принимается внутри круга, наибольшее 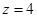 – на его границе.
– на его границе.
Найти экстремумы функции 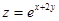 при условии , что
при условии , что 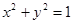 .
.
Решение.
Первый способ. При условии 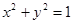 имеем
имеем 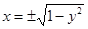 и получаем две функции одной переменной
и получаем две функции одной переменной 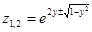 ;
; 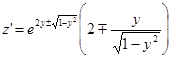 .
.
Критические точки задаются равенствами 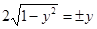 , т.е.
, т.е. 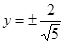 . Таким образом, имеем две критические точки
. Таким образом, имеем две критические точки 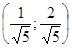 и
и 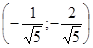 .
.
Легко проверить, что 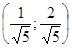 – точка максимума и
– точка максимума и 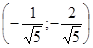 – точка минимума.
– точка минимума.
Второй способ. Функция Лагранжа (15.8) имеет вид:
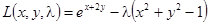 . (15.8)
. (15.8)
Приравнивая ее частные производные к нулю, получаем систему:
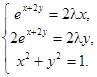
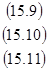
Из уравнений (15.9) и (15.10) находим 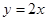 ,подставляя в (15.11), получаем два решения
,подставляя в (15.11), получаем два решения 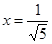 ,
, 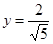 и
и 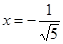 ,
, 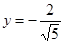 . Таким образом, получаем те же две критические точки
. Таким образом, получаем те же две критические точки 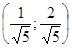 – точку максимума и
– точку максимума и 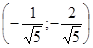 – точку минимума.
– точку минимума.
Исследовать функции на экстремум:
1. 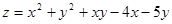 . 2.
. 2. 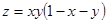 . 3.
. 3. 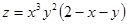 .
.
4. 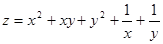 . 5.
. 5. 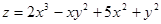 . 6.
. 6. 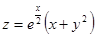 .
.
7 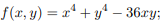 8
8 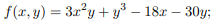
9 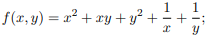 10
10 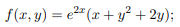
Найти наибольшее и наименьшее значения функции в областях, задаваемых неравенствами:
11. 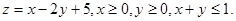 12.
12. 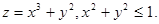 .
.
13. 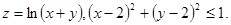
Найти наибольшее значение функции f(x, y) в квадрате [0, 1] × [0, 1]
14 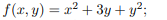 15
15 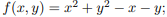 16
16 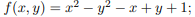
17 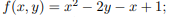 18
18 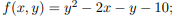 19
19 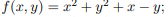
20 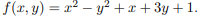
4.. Метод наименьших квадратов
Краткая теория
1. Постановка задачи. Производится n наблюдений 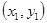 ,...,
,..., 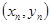 переменных х и у. Предполагая, что между х и у существует зависимость вида
переменных х и у. Предполагая, что между х и у существует зависимость вида 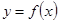 ,найти значения параметров а и b,наилучшим образом согласованные с экспериментальными данными.
,найти значения параметров а и b,наилучшим образом согласованные с экспериментальными данными.
Согласно методу наименьших квадратов параметры функции 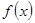 следует выбирать так, чтобы сумма квадратов невязок
следует выбирать так, чтобы сумма квадратов невязок 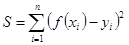 (15.14)
(15.14)
была наименьшей.
2.Если 
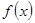 – линейная функция, т.е.
– линейная функция, т.е. 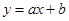 , то
, то 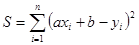 , а неизвестные параметры а и b определяются из системы нормальных уравнений:
, а неизвестные параметры а и b определяются из системы нормальных уравнений:
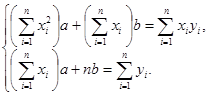 (15.15)
(15.15)
3.Если 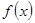 – квадратичная функция, т.е.
– квадратичная функция, т.е. 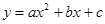 , то
, то 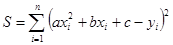 , а неизвестные параметры а, b, с определяются из системы нормальных уравнений:
, а неизвестные параметры а, b, с определяются из системы нормальных уравнений:
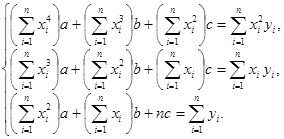 (15.16)
(15.16)
15.88. Имеются следующие данные о величине пробега автомобиля х (тыс. км) и у – расходе масла (л/тыс. км):
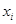
| 50 | 70 | 90 | 110 | 130 |
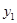
| 0,2 | 0,5 | 0,8 | 1,1 | 1,3 |
Полагая, что между переменными х и у существует линейная зависимость, найти эмпирическую формулу 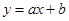 методом наименьших квадратов.
методом наименьших квадратов.
Решение. Найдем необходимые для решения суммы 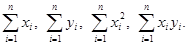
Промежуточные вычисления представлены в таблице:
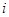
| 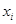
| 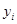
| 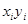
| 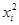
|
| 1 | 50 | 0,2 | 10 | 2500 |
| 2 | 70 | 0,5 | 35 | 4900 |
| 3 | 90 | 0,8 | 72 | 8100 |
| 4 | 110 | 1,1 | 121 | 12100 |
| 5 | 130 | 1,3 | 169 | 16900 |
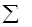
| 450 | 3,9 | 407 | 44500 |
Система нормальных уравнений (15.15) имеет вид:
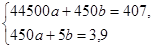
Ее решения 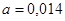 ,
, 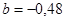 . Таким образом, линейная зависимость имеет вид:
. Таким образом, линейная зависимость имеет вид: 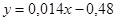 .
.
1. Имеется шесть измерений пары переменных 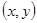 , результаты которых приведены в таблице:
, результаты которых приведены в таблице:
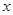
| 1 | 2 | 3 | 4 |
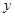
| 0,2 | 0,3 | 1,0 | 1,2 |
Методом наименьших квадратов построить линейную зависимость 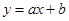 . Сравнить полученную зависимость с зависимостью
. Сравнить полученную зависимость с зависимостью 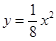 .
.
2. Имеются следующие данные о расходах на рекламу х (тыс. усл, ед.) и сбыте продукции у (тыс. ед.):
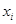
| 1 | 2 | 3 | 4 | 5 |
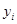
| 1,6 | 4,0 | 7,4 | 12,0 | 18,0 |
Предполагая, что между переменными х и у существует квадратичная зависимость вида 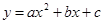 , найти значения параметров а, b, с методом наименьших квадратов.
, найти значения параметров а, b, с методом наименьших квадратов.
3. х -цена на товар (усл.ед.);у –уровень продаж (тыс.ед.):
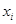
| 3,0 | 4,0 | 5,0 | 6,0 | 7,0 |
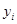
| 200 | 160 | 120 | 90 | 80 |
4. х -уровень потребления электроэнергии на предприятии (млн кВт. ч);у –себестоимость единицы продукции:
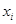
| 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
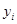
| 20,0 | 18,8 | 18,2 | 18,1 | 18,0 |
5. х -мощность двигателя (л.с.);у –средний срок его эксплуатации (мес.):
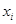
| 30 | 40 | 50 | 60 | 70 |
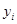
| 18 | 20 | 21 | 24 | 25 |
По экспериментальным данным построить методом наименьших квадратов
линейную эмпирическую зависимость 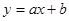 . Сравнить полученную зависимость с альтернативной и определить, какая из них лучше соответствует экспериментальным данным:
. Сравнить полученную зависимость с альтернативной и определить, какая из них лучше соответствует экспериментальным данным:
6.
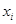
| 2 | 2,5 | 3 | 3,5 | 4 |
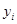
| 4,2 | 5,5 | 6,9 | 8 | 9,5 |
Альтернативная зависимость 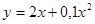 .
.
7.
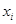
| 1 | 2 | 3 | 4 | 5 |
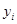
| 1,0 | 1,4 | 1,7 | 2,0 | 2,2 |
Альтернативная зависимость 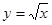 .
.
8.
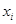
| 1,0 | 1,5 | 2,0 | 2,5 | 3,0 |
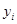
| 0,50 | 0,30 | 0,25 | 0,18 | 0,12 |
Альтернативная зависимость 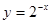 .
.
9. Имеютсяследующие экспериментальные данные о количестве единиц произведенной продукции х и издержках у (тыс.усл.ед.):
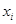
| 10 | 20 | 30 | 40 | 50 |
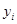
| 2,0 | 5,9 | 12,0 | 20,0 | 30,0 |
Функция издержек ищется в виде 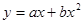 . Определить параметры а и b функции методом наименьших квадратов.
. Определить параметры а и b функции методом наименьших квадратов.
10. Имеютсяследующие экспериментальные данные о количестве произведенного товара х (тыс.ед.) и количестве реализованного товара К(х) (тыс.ед.):
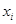
| 100 | 120 | 140 | 160 | 180 | 200 |
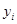
| 100 | 114 | 130 | 146 | 163 | 180 |
Зависимость ищется в виде 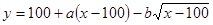 . Найти ее параметры а и b функции методом наименьших квадратов.
. Найти ее параметры а и b функции методом наименьших квадратов.
5. Двойные интегралы
Краткая теория
 1. Рассмотрим множество D на плоскости. Построим покрывающую это множество решетку (рис. 15.5).
1. Рассмотрим множество D на плоскости. Построим покрывающую это множество решетку (рис. 15.5).
Пусть 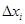 и
и 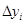 – соответственно длина горизонтальной и вертикальной клетки
– соответственно длина горизонтальной и вертикальной клетки 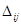 . Выберем в каждой клетке
. Выберем в каждой клетке 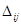 точку
точку 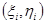 .
.
Интегральной суммой функции 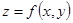 на множестве D называется сумма
на множестве D называется сумма
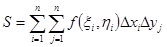 .
.
2.Функция 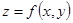 называется, интегрируемой на множестве D, если существует конечный предел I интегральной суммы этой функции на D при условии
называется, интегрируемой на множестве D, если существует конечный предел I интегральной суммы этой функции на D при условии 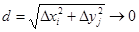 . Само значение предела I называется двойным интегралом функции
. Само значение предела I называется двойным интегралом функции 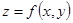 на множестве D:
на множестве D:
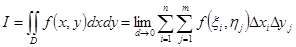 . (15.17)
. (15.17)
3.Если область D имеет вид, изображенный на рис. 15.6,
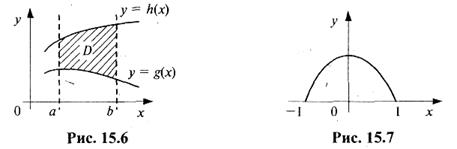
то имеет место равенство
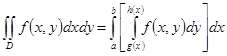 . (15.18)
. (15.18)
Вычислить 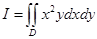 , где D – полукруг, изображенный на рис. 15.7.
, где D – полукруг, изображенный на рис. 15.7.
Решение. Имеем 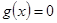 ,
, 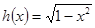 – функции, задающие нижнюю и верхнюю границы области.
– функции, задающие нижнюю и верхнюю границы области.
По формуле (15.18):
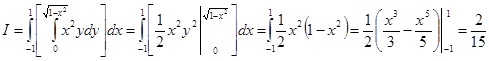 .
.
Вычислить 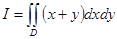 , где D – область, ограниченная параболами
, где D – область, ограниченная параболами 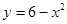 ,
, 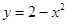 , прямой
, прямой 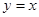 и осью ординат.
и осью ординат.
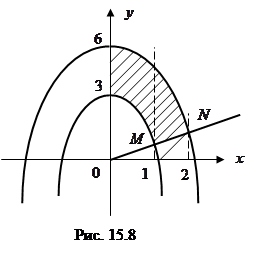 Решение. Область D изображена на рис. 15.8.
Решение. Область D изображена на рис. 15.8.
Разобьем область D на две области прямой, проходящей через точку М параллельно оси ординат. Точка М имеет абсциссу, равную 1, точка N – равную 2. Таким образом, имеем:
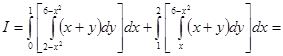
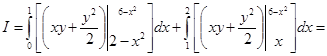
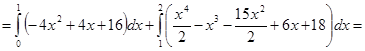
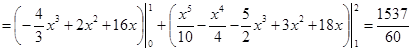 .
.
Вычислить двойные интегралы:
1. 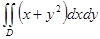 , где D ограничена прямыми у = х, у = 2х и у = -х + 4.
, где D ограничена прямыми у = х, у = 2х и у = -х + 4.
2. 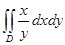 , где D ограничена прямыми
, где D ограничена прямыми 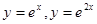 и прямой х = 2.
и прямой х = 2.
3. 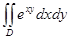 , где D ограничена гиперболой ху = 1, осью абсцисс и прямыми х = 2, х = 3.
, где D ограничена гиперболой ху = 1, осью абсцисс и прямыми х = 2, х = 3.
4. 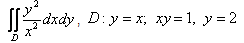
5. 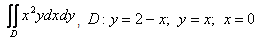
6. 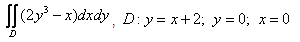
7. 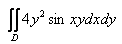
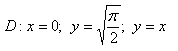
8. 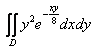
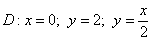
9. 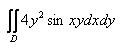
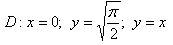
10. 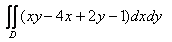
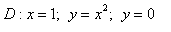
6. Функции нескольких переменных в экономических задачах
Краткая теория
1. Производственной функцией называется зависимость результата производственной деятельности – выпуска продукции и от обусловивших его факторов – затрат ресурсов х1, х2,…, х n. Производственная функция может быть задана как в натуральных, так и в денежных единицах. В последнем случае она представляет собой доход от использования ресурсов.
Производственная функция 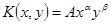 называется функцией Кобба-Дугласа. Параметры
называется функцией Кобба-Дугласа. Параметры 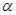 и
и 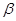 представляют собой частные эластичности выпуска продукции по отношению к затратам труда х и капитала y (см. п. 3).
представляют собой частные эластичности выпуска продукции по отношению к затратам труда х и капитала y (см. п. 3).
2. Функция полезности U(х1, х2, …, х n)задает полезность для потребителя от приобретения х1единиц 1-го блага, 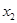 единиц 2-го блага и т.д.
единиц 2-го блага и т.д.
3. Частной эластичностью функции нескольких переменных 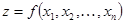 относительно переменной х i, называется величина
относительно переменной х i, называется величина
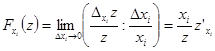 (15.19)
(15.19)
Значение 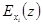 показывает приближенно, на сколько процентов изменится переменная z при изменении переменной xi, на 1 %.
показывает приближенно, на сколько процентов изменится переменная z при изменении переменной xi, на 1 %.
Производственная функция (в денежном выражении) имеет вид 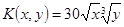 (х – количество единиц первого ресурса, у – второго). Стоимость единицы первого ресурса – 5, второго – 10 ден. ед. Найти максимальную прибыль при использовании ресурсов.
(х – количество единиц первого ресурса, у – второго). Стоимость единицы первого ресурса – 5, второго – 10 ден. ед. Найти максимальную прибыль при использовании ресурсов.
Решение. Производственная функция в денежном выражении равна доходу от использования ресурсов. Издержки при этом равны С(х) = 5х + 10 у. Функция прибыли равна 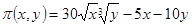 . Требуется найти ее максимум.
. Требуется найти ее максимум.
Частные производные функции 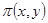 равны
равны 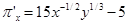 ;
; 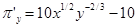 . Приравнивая их к нулю, найдем решение х = 81, у = 27. Частные производные второго порядка имеют вид:
. Приравнивая их к нулю, найдем решение х = 81, у = 27. Частные производные второго порядка имеют вид:
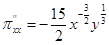 ,
, 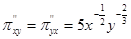 ,
, 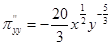
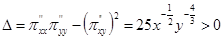 ,
, 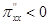 .
.
Таким образом, найденная критическая точка есть точка максимума. Соответствующее значение прибыли равно 135 (ден. ед.).
Производственная функция равна 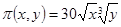 , стоимость единицы первого ресурса равна 5, второго – 10. В силу бюджетных ограничений на ресурсы может быть потрачено не более 600ден. ед. В этих условиях найти оптимальное для производителя значение (х, у)количества используемых ресурсов.
, стоимость единицы первого ресурса равна 5, второго – 10. В силу бюджетных ограничений на ресурсы может быть потрачено не более 600ден. ед. В этих условиях найти оптимальное для производителя значение (х, у)количества используемых ресурсов.
Решение. Теперь следует максимизировать функцию 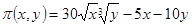 , но при условии, что
, но при условии, что 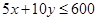 . В предыдущей задаче было найдено оптимальное распределение ресурсов в ситуации, когда ограничения отсутствовали. Оказалось, что оптимальные затраты на ресурсы равны
. В предыдущей задаче было найдено оптимальное распределение ресурсов в ситуации, когда ограничения отсутствовали. Оказалось, что оптимальные затраты на ресурсы равны 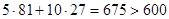 . Можно показать, что в этом случае в условиях наличия ограничений на ресурсы следует потратить всю возможную сумму.
. Можно показать, что в этом случае в условиях наличия ограничений на ресурсы следует потратить всю возможную сумму.
Итак, имеем задачу максимизации функции 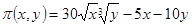
при условии, что 5х + 10у = 600, или х + 2у = 120.
Первый способ. В силу ограничений имеем х = 120 – 2у и
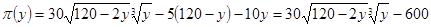 .
.
Производная функции 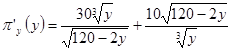 . Приравнивая ее к нулю, получим решение у = 24, откуда
. Приравнивая ее к нулю, получим решение у = 24, откуда 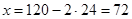 . Максимальная прибыль при этом равна
. Максимальная прибыль при этом равна 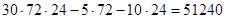 (ден. ед.).
(ден. ед.).
Второй способ. При условии, что 5х + 10у = 600, функция прибыли имеет вид 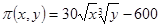 . Очевидно, что если какое-то значение С уровня функции
. Очевидно, что если какое-то значение С уровня функции 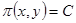 должна пересекаться с прямой 5x + 10y = 600.
должна пересекаться с прямой 5x + 10y = 600.
Уравнение линии уровня функции прибыли 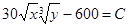 может быть записано как
может быть записано как 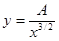 , где
, где 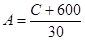 .
.
Легко видеть, что максимальное значение А,а следовательно, и уровня С достигается в том случае, если соответствующая линия уровня касается прямой 5х + 10у = 600. Так как градиент в каждой точке ортогонален линии уровня, то из этого следует, что условие максимальности прибыли может быть сформулировано следующим образом: вектор 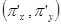 ортогонален прямой 5х + 10у = 600. Эта прямая имеет угловой коэффициент, равный
ортогонален прямой 5х + 10у = 600. Эта прямая имеет угловой коэффициент, равный 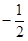 . Угловой коэффициент прямой, проходящей через вектор
. Угловой коэффициент прямой, проходящей через вектор 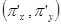 равен
равен 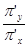 . По условию перпендикулярности прямых имеем
. По условию перпендикулярности прямых имеем 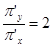 ,
,
т.е. 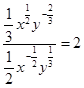 или
или 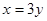 . Подставляя полученное выражение в уравнение
. Подставляя полученное выражение в уравнение
прямой 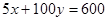 , находим х = 72, у = 24.
, находим х = 72, у = 24.
Замечание. Оптимальное решение лежит на прямой ограничений (в данном случае на прямой 5х + 10у = 600) только в том случае, если при оптимальном решении без ограничений сумма, затрачиваемая на ресурсы, больше ограничительной. В противном случае решение задачи с ограничениями просто совпадает с решением задачи без ограничений.
Функция полезности имеет вид: 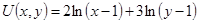 . Цена единицы первого блага равна 8, второго – 16. На приобретение этих благ может быть затрачена сумма, равная 1000. Как следует распределить эту сумму между двумя благами, чтобы полезность от их приобретения была бы наибольшей?
. Цена единицы первого блага равна 8, второго – 16. На приобретение этих благ может быть затрачена сумма, равная 1000. Как следует распределить эту сумму между двумя благами, чтобы полезность от их приобретения была бы наибольшей?
Решение. Рассмотрим линии уровня функции полезности 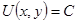 , т.е.
, т.е. 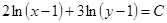 . Используя свойства логарифмов, имеем:
. Используя свойства логарифмов, имеем: 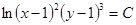 , т.е.
, т.е. 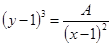 , где
, где 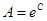 .
.
Таким образом, линии уровня представляют собой графики функции
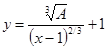 .
.
Используя рассуждения, приведенные в предыдущем примере, получаем, что в точке (х, у), в которой достигается максимальная полезность, линия уровня касается прямой 8x + 16у = 1000, или х + 2у = 125. Значит, градиент функции полезности должен быть перпендикулярен этой линии. Градиент функции полезности имеетвид 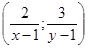 . Угловой коэффициент прямой
. Угловой коэффициент прямой 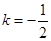 . Используяусловие перпендикулярности прямых, имеем:
. Используяусловие перпендикулярности прямых, имеем: 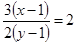 или
или 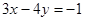 .
.
Следовательно, оптимальное распределение потребления товаров находится как решение системы:
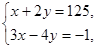 т.е. x = 49,5; y = 37,75.
т.е. x = 49,5; y = 37,75.
Найти значения величин используемых ресурсов (х,у), при которых фирма-производитель получит максимальную прибыль, если заданы производственная функция
К(х,у) и цены 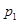 и
и 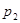 на единицу первого и второго ресурсов:
на единицу первого и второго ресурсов:
1. 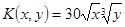 ;
; 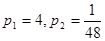 .
.
2. 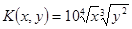 ;
; 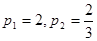 .
.
Заданы производственная функция, цены на единицу первого и второго ресурсов, а также ограничения I в сумме, которая может быть потрачена на приобретение ресурсов (сумма 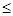 I). Найти значения величин используемых ресурсов (х,у), при которых фирма-производитель получит наибольшую прибыль:
I). Найти значения величин используемых ресурсов (х,у), при которых фирма-производитель получит наибольшую прибыль:
3. 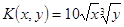 ;
; 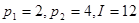 .
.
4. 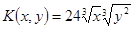 ;
; 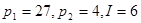 .
.
Потребитель имеет возможность потратить сумму 1000 ден.ед. на приобретение х единиц первого товара и у единиц второго товара. Заданы функция полезности U(х,у) и цены 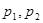 за единицу соответственно первого и второго товаров. Найти значения (х,у), при которых полезность для потребителя будет наибольшей:
за единицу соответственно первого и второго товаров. Найти значения (х,у), при которых полезность для потребителя будет наибольшей:
5. 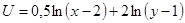 ;
; 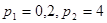 .
.
6. 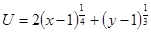 ;
; 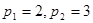 .
.
7. Оптимальный набор потребителя составляет 6 единиц продукта х1 и 8 единиц продукта х2 . Определите цены потребляемых благ, если известно, что доход потребителя 240 у. е., и он собирается его истратить весь, а функция полезности имеет вид: u(x1 , x2 ) = х1 х2 .
8. Фирма производит два вида товаров: А и В. Для производства х единиц товара А и у единиц товара В требуется заранее приобрести g (x,y) = x + y - x2y2 (кг) сырья. Из-за ограничений на объем хранилища количество сырья не должно превышать 2100 кг. Доход от реализации единицы товара А составляет 2000 у. е., а от реализации единицы товара В ‒ 1000 у. е. Определить план выпуска продукции, максимизирующей доход
9. При составлении суточного рациона кормления животных можно использовать свежее сено (не более 50 кг) и силос (не более 85 кг). Рацион должен обладать определенной питательностью (число кормовых единиц не менее 30) и содержать питательные вещества: белок (не менее 1 кг), кальций (не менее 100 г) и фосфор (не менее 80 г). Определить оптимальный рацион из условия минимизации себестоимости. Данные о содержании питательных веществ в 1 кг каждого продукта и об их себестоимости приведены в таблице:

10. Фирма реализует автомобили двумя способами: через оптовую и розничную торговлю. При реализации х автомобилей в розницу расходы на реализацию составляют 4х + х2 у. е., а при продаже у автомобилей оптом ‒ у2 у. е. Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число предназначенных для продажи автомобилей составляет 200 шт
Комплексные числа
Краткая теория
1. Комплексным числомназывается выражение вида 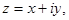 где
где 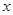 и
и 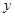 - действительные числа,
- действительные числа, 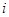 - мнимая единица.
- мнимая единица.
Два комплексных числа 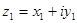 и
и 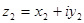 равны, если
равны, если 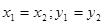 .
.
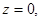 если
если 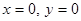
Дата добавления: 2021-04-15; просмотров: 294; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
