Результаты аналитического решения радиальных задач
Аналитическое решение уравнения Шредингера (6.15) позволяет найти собственные функции и уровни энергии при любом l. Результаты решения имеют одну интересную особенность. Оказывается, что каждое собственное значение энергии любой задачи с l > 0 (р-, d-, f- задачи и т.д.) обязательно совпадает с одним из собственных значений s-задачи:
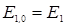
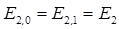
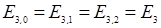
|
. . . . . . . . . . .
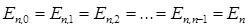 (6.24)
(6.24)
При этом Еn выражается простой формулой, известной еще из модельной теории Бора
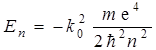 , ,
| (6.25) |
где n – главное квантовое число, принимающее значения
n = 1, 2, 3,...
Что касается орбитального квантового числа l, то, очевидно, его значение не может превышать n – 1:
l = 0, 1, 2,..., n – 1.
Совпадение собственных значений для разных квантовых состояний, описываемых разными собственными функциями, носит название вырождения, а такие собственные значения называются вырожденными. В случае атома водорода вырождение уровней энергии по орбитальному квантовому числу является специфическим. Оно имеет место именно тогда, когда потенциальная энергия взаимодействия электрона с ядром убывает обратно пропорционально первой степени расстояния между ними (что соответствует закону Кулона). В связи с этим вырождение уровней энергии в атоме водорода называют кулоновским. В многоэлектронных атомах зависимость потенциальной энергии электрона от r из-за взаимодействия электронов друг с другом оказывается иной, и поэтому вырождение энергии по орбитальному квантовому числу исчезает – «снимается».
Таким образом, в атоме водорода уровню энергии E n отвечает не одна, а n различных радиальных функций:
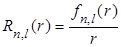 , l = 0, 1, 2,..., n – 1. , l = 0, 1, 2,..., n – 1.
| (6.26) |
Явные выражения для 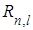 удобно представлять как функции от безразмерной координаты
удобно представлять как функции от безразмерной координаты
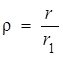
| (6.27) |
где 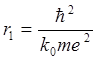 есть (первый) боровский радиус. Тогда, как показывает анализ,
есть (первый) боровский радиус. Тогда, как показывает анализ,
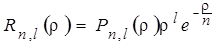
| (6.28) |
где 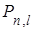 есть полином степени n – l – 1, который определяет число узлов радиальной функции (т.е. число ее прохождений через нуль), сомножитель
есть полином степени n – l – 1, который определяет число узлов радиальной функции (т.е. число ее прохождений через нуль), сомножитель 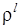
 определяет поведение этой функции при малых ρ, т.е. возле атомного ядра, а экспоненциальный множитель
определяет поведение этой функции при малых ρ, т.е. возле атомного ядра, а экспоненциальный множитель 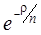 – ее поведение на периферии атома.
– ее поведение на периферии атома.
Волновые функции и распределение
Электронной плотности
В соответствии с (6.11) и (6.26), волновая функция электрона в атоме водорода представляет собой произведение трех функций
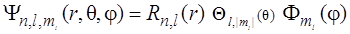
|
а ее вид определяется тремя квантовыми числами n, l, m l, в то время как энергия атома зависит только от главного квантового числа n. В результате, уровню энергии Еn отвечает не одна, а несколько волновых функций, число которых можно найти, суммируя число состояний при заданных n и l по всем l от 0 до n –1:
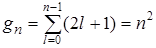
| (6.29) |
Это означает, что кратность вырождения g n уровней энергии атома водорода (без учета спина электрона) равна n2.
Волновые функции определяют распределение вероятности для любой физической величины. В частности, вероятность нахождения электрона в некоторой бесконечно малой области с объемом dV равна
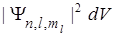
и, следовательно, квадрат модуля волновой функции имеет смысл объемной плотности вероятности, которую часто называют электронной плотностью.
Из уравнения Шредингера (6.2) волновую функцию можно найти лишь с точностью до постоянного коэффициента. Этот коэффициент С определяют из условия нормировки:
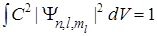 .
.
Интеграл берется по всему пространству. Элемент объема в сферических координатах имеет вид
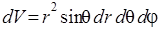 .
.
Если учесть, что 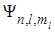 является произведением трех функций, условие нормировки можно записать:
является произведением трех функций, условие нормировки можно записать:
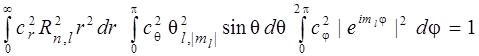 .
.
Приравнивая каждый из входящих в это выражение интегралов единице, находят значение трех нормировочных коэффициентов 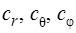 , причем
, причем 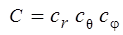 .
.
Поскольку 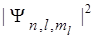 не зависит от φ (т.к.
не зависит от φ (т.к. 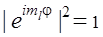 ), объемные распределения электронной плотности («электронные облака») для всех состояний представляют собой тела вращения вокруг оси Z. В случае s-состояний полярная функция
), объемные распределения электронной плотности («электронные облака») для всех состояний представляют собой тела вращения вокруг оси Z. В случае s-состояний полярная функция 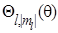 сводится к постоянной, что приводит к сферической симметрии электронной плотности этих состояний. Однако в других состояниях угловые распределения электронной плотности неизотропны; их форма усложняется по мере увеличения числа l.
сводится к постоянной, что приводит к сферической симметрии электронной плотности этих состояний. Однако в других состояниях угловые распределения электронной плотности неизотропны; их форма усложняется по мере увеличения числа l.
Важную роль играет распределение радиальной электронной плотности. Чтобы получить формулу для этого распределения, необходимо найти вероятность dW(r) нахождения электрона в шаровом слое толщиной dr:
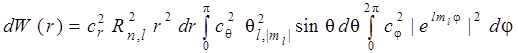 .
.
Для нормированных волновых функций, входящие в это выражение интегралы равны единице, и, следовательно,
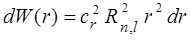 ,
,
так что радиальная плотность вероятности dW(r)/dr распределена в соответствии с соотношением:
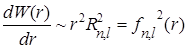 .
.
Наиболее простым это распределение оказывается для состояний с максимально возможным для данного n значением числа l = n – 1. Оно имеет один максимум, удаленный от центра на расстояние 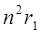 , так что в состоянии 1s наиболее вероятное значение r в точности равно первому боровскому радиусу r1. Вообще же в распределении радиальной электронной плотности может быть несколько максимумов, количество которых определяется квантовыми числами n и l.
, так что в состоянии 1s наиболее вероятное значение r в точности равно первому боровскому радиусу r1. Вообще же в распределении радиальной электронной плотности может быть несколько максимумов, количество которых определяется квантовыми числами n и l.
Дата добавления: 2021-04-05; просмотров: 44; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
