Качественный анализ одномерных радиальных задач
Международный государственный экологический
институт им. А.Д. Сахарова. БГУ
Факультет мониторинга окружающей среды
Кафедра общей и медицинской физики
Лабораторная работа № 5.6 (К)
КВАНТОВАНИЕ энергии и волновые функции электрона в атоме водорода
Минск
2018
КВАНТОВАНИЕ энергии и волновые функции электрона в атоме водорода
Цель работы:нахождение уровней энергии и радиальных волновых функций атома водорода путем численного решения стационарного уравнения Шредингера; изучение расположения уровней энергии и радиального распределения электронной плотности в зависимости от квантовых чисел n и l.
Постановка задачи об атоме водорода
В квантовой механике
Атом водорода состоит из ядра, обладающего зарядом +е и массой M, и электрона ( –е , m ). Поскольку M >> m, будем считать ядро покоящимся. Кулоновскому притяжению ядра и электрона соответствует потенциальная функция
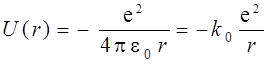, (6.1)
где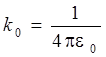 
– электрическая постоянная, r – расстояние от ядра до электрона (модуль радиус-вектора 
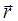). Тот факт, что U зависит только от r, означает, что задача обладает сферической симметрией. В связи с этим будем решать задачу о поведении электрона в атоме водорода в сферических координатах r, θ, φ, с началом координат, совпадающим с положением ядра. В этих координатах стационарное уравнение Шредингера примет вид
|
|
|
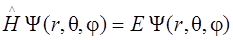, (6.2)
где Ψ(r, θ, φ) – волновая функция электрона, E – его полная энергия,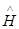 
– оператор Гамильтона, равный
 .
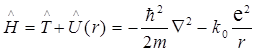| (6.3) |
Поскольку оператор кинетической энергии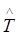 
связан с оператором квадрата момента импульса 
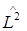соотношением
 ,
|
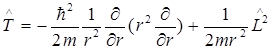оператор Гамильтона атома водорода можно представить в виде
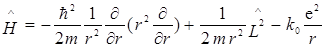. (6.4)
Одномерное уравнение Шредингера
Для радиальной функции
Известно, что при движении частицы в статическом силовом поле сохраняется ее полная энергия Е, а если оно обладает также и центральной симметрией, то и момент импульса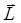 
. В классической механике это означает, что четыре величины E, Lx , Ly и Lz имеют определенные, не изменяющиеся во времени значения. В квантовой механике центральная симметрия задачи приводит к тому, что в стационарных состояниях кроме энергии E могут иметь определенные постоянные значения только две величины: квадрат момента импульса 
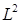и лишь одна из его проекций, например, Lz. В таких состояниях волновая функция должна удовлетворять, кроме уравнения Шредингера для стационарных состояний (6.2), еще и уравнениям на собственные значения операторов 
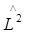и 
:
|
|
|
 ,
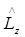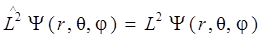| (6.5) |
 .
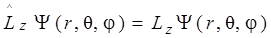| (6.6) |
Свойства операторов 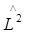и 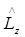, таковы, что физически приемлемые решения уравнений (6.5), (6.6) имеют место лишь для следующих значений 
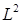и Lz:
 ,
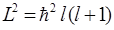| (6.7) |
 ,
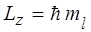| (6.8) |
т. е. для собственных значений операторовквадрата углового момента и его проекции. Число l называют орбитальным квантовым числом; оно принимает одно из значений:
| l = 0, 1, 2,… | (6.9) |
Число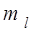 
называют магнитным орбитальным квантовым числом, причем при заданном l
 .
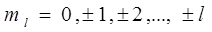| (6.10) |
Решениями уравнений (6.5) и (6.6) являются собственные функции операторов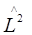 
и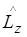 
, имеющие вид, зависящий от квантовых чисел l и m l :
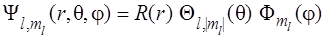
| (6.11) |
Квантовые состояния атома, отвечающие различным значениям орбитального квантового числа l, принято обозначать латинскими буквами: s-состояние (l = 0), p-состояние (l = 1), d-состояние (l = 2), f-состояние (l = 3) и далее по алфавиту.
Как видно из (6.11) собственные функции операторов 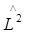и 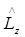, представляют собой произведения трех функций: радиальной, полярной и азимутальной. Каждая из них является функцией одной из сферических координат. Азимутальная функция имеет вид
.
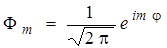Явный вид полярной функции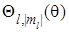 
приводится в книгах по атомной физике и квантовой механике.
Что же касается радиальной функции R (r), то уравнения (6.5) и (6.6) ее не определяют. Согласно постановке задачи она может быть найдена из условия, чтобы функция (6.11) удовлетворяла уравнению Шредингера (6.2), т. е была собственной функцией оператора Гамильтона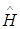 
. Подставляя (6.11) в (6.2) с гамильтонианом 
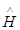(6.4) и учитывая (6.5), легко получить уравнение для радиальной функции
|
|
|
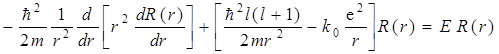
| (6.12) |
Его можно упростить, вводя новую функцию
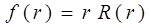
| (6.13) |
и используя обозначение
 .
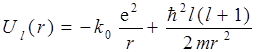| (6.14) |
В результате уравнение (6.12) примет вид стационарного уравнения Шредингера одномерной задачи:
 ,
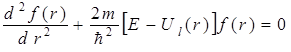| (6.15) |
в котором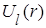 
имеет смысл эффективной потенциальной энергии. Кроме кулоновской энергии, выражение (6.14) содержит так называемую центробежную энергию
 .
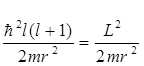| (6.16) |
Хотя центробежная энергия является частью кинетической энергии электрона, ее зависимость от координаты r дает формальные основания включить ее в потенциальную функцию.
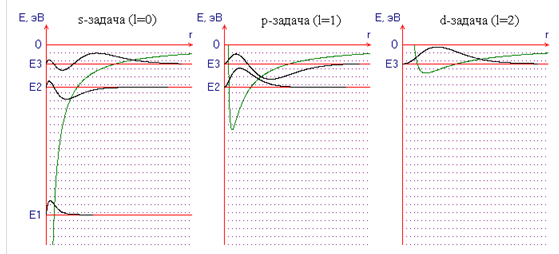Рис. 6.1
Таким образом, трехмерная квантовомеханическая задача о поведении электрона в атоме водорода сводится к набору одномерных квантовых задач с разными потенциальными ямами (рис. 6.1), которые соответствуют разным значениям орбитального квантового числа ( s-задача, р-задача, d-задача и т.д.).
|
|
|
Кроме потенциальных ям на рис. 6.1 представлены графики радиаль-ных функций f ( r ), а также соответствующие им уровни энергии En .
Качественный анализ одномерных радиальных задач
Характер потенциальных кривых (Рис. 6.1) говорит о том, что квантование будет иметь место лишь для отрицательных значений энергии Е, поскольку именно для E < 0 движение электрона является финитным и соответствует связанным состояниям атома. При положительных энергиях (Е > 0) движение инфинитно (атом ионизован), и квантования энергии нет.
Чтобы волновая функция (6.11) оставалась конечной при r → 0, необходимо выполнение граничного условия f (r =0) = 0. Его можно трактовать, как наличие бесконечно высокой непроницаемой потенциальной стенки при r = 0 и как запрет проникновения в «область» r < 0.
Если в случае s-ямы классически разрешенная для движения электрона (при заданной полной энергии E) область доходит до начала координат (r = 0), то во всех ямах с l ≠ 0 ее левая граница rл (определяемая условием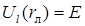 
), будет тем дальше от начала координат, чем больше значение орбитального квантового числа.
В классически запрещенной области волновая функция f(r), соответствующая физически приемлемым решениям, быстро затухает. Поэтому при r → 0 в случае р- и d-ям функция f(r) убывает значительно быстрее, чем в случае s-ямы, где f(r) сохраняет осциллирующий характер вплоть до r = 0. В результате, радиальная функция R(r) ведет себя в центре атома по-разному для s-состояний и состояний с отличным от нуля орбитальным моментом:
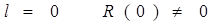при  ,
при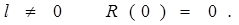 
| (6.17) |
Такое поведение радиальной функции R(r) вблизи ядра можно объяснить действием центробежной отталкивающей силы, которой отвечает эффективная потенциальная энергия вида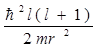 
.
В классически разрешенной области функция f(r) имеет осциллирующий характер, причем амплитуда и эффективная длина волны этих осцилляций сами изменяются с ростом r . При этом физически приемлемым решениям соответствует размещение в указанной области целого числа полуволн (начиная с одной полуволны). Решение s-задачи приводит к собственным функциям
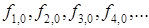
| (6.18) |
и отвечающим им собственным значениям оператора Гамильтона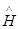 
– дискретным уровням энергии
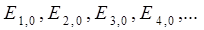
| (6.19) |
Решение р-задачи (l = 1 ) дает свои собственные функции и уровни энергии, которые принято обозначать как
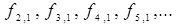
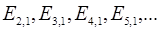
| (6.20) (6.21) |
т.е. начинать их нумерацию с числа 2. Аналогично, для d-задачи получится:
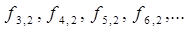
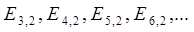
| (6.22) (6.23) |
Такой способ обозначений соответствует тому, что, по определению, главное квантовое числоn вводится как число, нумерующее уровни энергии в каждой из потенциальных l-ям в порядке возрастания энергии, начиная со значения n = l + 1.
Чем больше орбитальное квантовое число l, тем мельче оказывается соответствующая потенциальная яма, а ее уровни энергии начинаются со все больших величин, асимптотически приближаясь при l → ∞ к верхней границе энергий связанных состояний (границе ионизации, E = 0).
Дата добавления: 2021-04-05; просмотров: 45; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!