Равносильные преобразования уравнений

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Особый интерес представляют преобразования уравнений, дающие в результате их проведения равносильные уравнения, то есть, уравнения, имеющие то же множество корней, что и исходное уравнение. Такие преобразования называют равносильными преобразованиями. В школьных учебниках соответствующее определение не приводится в явном виде, но оно легко читается из контекста:

Определение

Равносильные преобразования уравнений – это преобразования, дающие равносильные уравнения.

Так чем же интересны равносильные преобразования? Тем, что если с их помощью удастся прийти от решаемого уравнения к довольно простому равносильному уравнению, то решение этого уравнения даст искомое решение исходного уравнения.

Из перечисленных в предыдущем пункте преобразований не все являются всегда равносильными. Некоторые преобразования являются равносильными лишь при определенных условиях. Составим список утверждений, которые определяют, какие преобразования и при каких условиях являются равносильными преобразованиями уравнения. Для этого за основу возьмем приведенный выше список, и к преобразованиям, которые не всегда равносильны, добавим условия, придающие им равносильность. Вот этот список:

· Замена выражения в левой или правой части уравнения тождественно равным ему выражением, при которой не изменяется ОДЗ переменных для уравнения, является равносильным преобразованием уравнения.

Поясним, почему это так. Для этого возьмем уравнение с одной переменной (аналогичные рассуждения можно провести и для уравнений с несколькими переменными) вида A(x)=B(x), выражения в его левой и правой части мы обозначили как A(x) и B(x) соответственно. Пусть выражение C(x) тождественно равно выражению A(x), причем ОДЗ переменной x уравнения C(x)=B(x) совпадает с ОДЗ переменной x для исходного уравнения. Докажем, что преобразование уравнения A(x)=B(x) в уравнение C(x)=B(x) есть равносильное преобразование, то есть, докажем, что уравнения A(x)=B(x) и C(x)=B(x) равносильные.

Для этого достаточно показать, что любой корень исходного уравнения является корнем уравнения C(x)=B(x), а любой корень уравнения C(x)=B(x) является корнем исходного уравнения.

Начнем с первой части. Пусть q – корень уравнения A(x)=B(x), тогда при подстановке его вместо x мы получим верное числовое равенство A(q)=B(q). Так как выражения A(x) и C(x) тождественно равны и выражение C(q) имеет смысл (это следует из условия о том, что ОДЗ для уравнения C(x)=B(x) совпадает с ОДЗ для исходного уравнения), то справедливо числовое равенство A(q)=C(q). Дальше используем свойства числовых равенств. В силу свойства симметричности равенство A(q)=C(q) можно переписать как C(q)=A(q). Тогда в силу свойства транзитивности из равенств C(q)=A(q) и A(q)=B(q) следует равенство C(q)=B(q). Этим доказано, что q – корень уравнения C(x)=B(x).

Абсолютно аналогично доказывается и вторая часть, а вместе с этим и все утверждение в целом.

Суть разобранного равносильного преобразования состоит в следующем: оно позволяет отдельно работать с выражениями в левой и правой части уравнений, заменяя их тождественно равными выражениями на исходной ОДЗ переменных.

Самый банальный пример: мы можем заменить сумму чисел в правой части уравнения x=2+1 ее значением, при этом получится равносильное уравнение вида x=3. Действительно, мы заменили выражение 2+1 тождественно равным ему выражением 3, и при этом не изменилась ОДЗ уравнения. Еще пример: в левой части уравнения 3·(x+2)=7·x−2·x+4−1 мы можем раскрыть скобки, а в правой – привести подобные слагаемые, что приведет нас к равносильному уравнению 3·x+6=5·x+3. Полученное уравнение действительно является равносильным, так как мы заменяли выражения тождественно равными им выражениями и при этом получили уравнение, имеющее ОДЗ, совпадающее с ОДЗ для исходного уравнения.

· Прибавление к обеим частям уравнения одного и того же числа или вычитание из обеих частей уравнения одного и того же числа есть равносильное преобразование уравнения.

Докажем, что прибавление к обеим частям уравнения A(x)=B(x) одного и того же числа c дает равносильное уравнение A(x)+c=B(x)+c и что вычитание из обеих частей уравнения A(x)=B(x) одного и того же числа c дает равносильное уравнение A(x)−c=B(x)−c.

Пусть q – корень уравнения A(x)=B(x), тогда справедливо равенство A(q)=B(q). Свойства числовых равенств нам позволяют прибавлять к обеим частям верного числового равенства или вычитать из его частей одно и то же число. Обозначим это число как c, тогда справедливы равенства A(q)+c=B(q)+c и A(q)−c=B(q)−c. Из этих равенств следует, что q – корень уравнения A(x)+c=B(x)+c и уравнения A(x)−c=B(x)−c.

Теперь обратно. Пусть q – корень уравнения A(x)+c=B(x)+c и уравнения A(x)−c=B(x)−c, тогда A(q)+c=B(q)+c и A(q)−c=B(q)−c. Мы знаем, что вычитание одного и того же числа из обеих частей верного числового равенства дает верное числовое равенство. Также мы знаем, что прибавление к обеим частям верного числового равенства дает верное числовое равенство. Вычтем из обеих частей верного числового равенства A(q)+c=B(q)+c число с, а к обеим частям равенства A(x)−c=B(x)−c прибавим число c. Это нам даст верные числовые равенства A(q)+c−c=B(q)+c−c и A(q)−c+c=B(q)+c−c, откуда заключаем, что A(q)=B(q). Из последнего равенства следует, что q – корень уравнения A(x)=B(x).

Так доказано исходное утверждение в целом.

Приведем пример такого преобразования уравнений. Возьмем уравнение x−3=1, и преобразуем его, прибавив к его обеим частям число 3, после этого мы получим уравнение x−3+3=1+3, которое равносильно исходному. Понятно, что в полученном уравнении можно выполнить действия с числами, о чем мы говорили в предыдущем пункте списка, в результате имеем уравнение x=4. Так, выполняя равносильные преобразования, мы невзначай решили уравнение x−3=1, его корень – это число 4. Рассмотренное равносильное преобразование очень часто используется для избавления от одинаковых числовых слагаемых, находящихся в разных частях уравнения. Например, и в левой и в правой частях уравнения x²+1=x+1 присутствует одинаковое слагаемое 1, вычитание из обеих частей уравнения числа 1 позволяет перейти к равносильному уравнению x²+1−1=x+1−1 и дальше к равносильному уравнению x²=x, и тем самым избавиться от этих одинаковых слагаемых.

· Прибавление к обеим частям уравнения или вычитание из обеих частей уравнения выражения, ОДЗ для которого не уже, чем ОДЗ для исходного уравнения, является равносильным преобразованием.

Докажем это утверждение. То есть, докажем, что уравнения A(x)=B(x) и A(x)+C(x)=B(x)+C(x) равносильные при условии, что ОДЗ для выражения C(x) не уже, чем ОДЗ для уравнения A(x)=B(x).

Сначала докажем один вспомогательный момент. Докажем, что при указанных условиях ОДЗ уравнений до и после преобразования одинаковые. Действительно, ОДЗ для уравнения A(x)+C(x)=B(x)+C(x) можно рассматривать как пересечение ОДЗ для уравнения A(x)=B(x) и ОДЗ для выражения C(x). Из этого и из того, что ОДЗ для выражения С(x) по условию не уже, чем ОДЗ для уравнения A(x)=B(x), следует, что ОДЗ для уравнений A(x)=B(x) и A(x)+C(x)=B(x)+C(x) одинаковые.

Теперь докажем равносильность уравнений A(x)=B(x) и A(x)+C(x)=B(x)+C(x) при условии, что области допустимых значений для этих уравнений одинаковые. Доказательство равносильности уравнений A(x)=B(x) и A(x)−C(x)=B(x)−C(x) при указанном условии приводить не будем, так как оно аналогично.

Пусть q – корень уравнения A(x)=B(x), тогда справедливо числовое равенство A(q)=B(q). Так как ОДЗ уравнений A(x)=B(x) и A(x)+C(x)=B(x)+C(x) одинаковые, то выражение C(x) имеет смысл при x=q, значит, C(q) – это некоторое число. Если прибавить C(q) к обеим частям верного числового равенства A(q)=B(q), то это даст верное числовое неравенство A(q)+C(q)=B(q)+C(q), из которого следует, что q – корень уравнения A(x)+C(x)=B(x)+C(x).

Обратно. Пусть q – корень уравнения A(x)+C(x)=B(x)+C(x), тогда A(q)+C(q)=B(q)+C(q) – верное числовое равенство. Мы знаем, что вычитание одного и того же числа из обеих частей верного числового равенства дает верное числовое равенство. Вычтем C(q) из обеих частей равенства A(q)+C(q)=B(q)+C(q), это дает A(q)+C(q)−C(q)=B(q)+C(q)−C(q) и дальше A(q)=B(q). Следовательно, q – корень уравнения A(x)=B(x).

Так рассматриваемое утверждение полностью доказано.

Приведем пример проведения этого преобразования. Возьмем уравнение 2·x+1=5·x+2. Мы можем прибавить к его обеим частям, например, выражение −x−1. Прибавление этого выражения не изменит ОДЗ, значит, такое преобразование является равносильным. В результате его проведения получим равносильное уравнение 2·x+1+(−x−1)=5·x+2+(−x−1). Это уравнение можно преобразовать дальше: раскрыть скобки и выполнить приведение подобных слагаемых в его левой и правой части (см. первый пункт списка). После выполнения этих действий мы получим равносильное уравнение x=4·x+1. Часто рассматриваемое преобразование уравнений применяется для избавления от одинаковых слагаемых, находящихся одновременно в левой и правой части уравнения.

· Если в уравнении перенести слагаемое из одной части в другую, изменив знак этого слагаемого на противоположный, то получится уравнение, равносильное данному.

Это утверждение является следствием предыдущих.

Покажем, как проводится это равносильное преобразование уравнения. Возьмем уравнение 3·x−1=2·x+3. Перенесем слагаемое, например, 2·x из правой части в левую, изменив его знак. При этом получим равносильное уравнение 3·x−1−2·x=3. Еще можно перенести минус единицу из левой части уравнения в правую, изменив знак на плюс: 3·x−2·x=3+1. Наконец, приведение подобных слагаемых приводит нас к равносильному уравнению x=4.

· Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число является равносильным преобразованием.

Приведем доказательство.

Пусть A(x)=B(x) – некоторое уравнение и c – некоторое число, отличное от нуля. Докажем, что умножение или деление обеих частей уравнения A(x)=B(x) на число c является равносильным преобразованием уравнения. Для этого докажем, что уравнения A(x)=B(x) и A(x)·c=B(x)·c, а также уравнения A(x)=B(x) и A(x):c=B(x):c - равносильные. Это можно сделать так: доказать, что любой корень уравнения A(x)=B(x) является корнем уравнения A(x)·c=B(x)·c и корнем уравнения A(x):c=B(x):c, после чего доказать, что любой корень уравнения A(x)·c=B(x)·c, как и любой корень уравнения A(x):c=B(x):c является корнем уравнения A(x)=B(x). Сделаем это.

Пусть q – корень уравнения A(x)=B(x). Тогда справедливо числовое равенство A(q)=B(q). Изучив свойства числовых равенств, мы узнали, что умножение или деление обеих частей верного числового равенства на одно и то же число, отличное от нуля, приводит к верному числовому равенству. Умножив обе части равенства A(q)=B(q) на c, получим верное числовое равенство A(q)·c=B(q)·c, из которого следует, что q – корень уравнения A(x)·c=B(x)·c. А разделив обе части равенства A(q)=B(q) на c, получим верное числовое равенство A(q):c=B(q):c, из которого следует, что q – корень уравнения A(x):c=B(x):c.

Теперь в другую сторону. Пусть q – корень уравнения A(x)·c=B(x)·c. Тогда A(q)·c=B(q)·c – верное числовое равенство. Разделив его обе части на отличное от нуля число c, получим верное числовое равенство A(q)·c:c=B(q)·c:c и дальше A(q)=B(q). Отсюда следует, что q – корень уравнения A(x)=B(x). Если q – корень уравнения A(x):c=B(x):c. Тогда A(q):c=B(q):c – верное числовое равенство. Умножив его обе части на отличное от нуля число c, получим верное числовое равенство A(q):c·c=B(q):c·c и дальше A(q)=B(q). Отсюда следует, что q – корень уравнения A(x)=B(x).

Утверждение доказано.

Приведем пример проведения этого преобразования. С его помощью можно, например, избавиться от дробей в уравнении 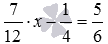. Для этого можно умножить обе части уравнения на 12. В результате получится равносильное уравнение вида 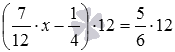, которое дальше можно преобразовать в равносильное уравнение 7·x−3=10, не содержащее в своей записи дробей.

· Умножение или деление обеих частей уравнения на одно и то же выражение, ОДЗ для которого не уже, чем ОДЗ для исходного уравнения и не обращающееся в нуль на ОДЗ для исходного уравнения, является равносильным преобразованием.

Докажем это утверждение. Для этого докажем, что если ОДЗ для выражения C(x) не уже, чем ОДЗ для уравнения A(x)=B(x), и C(x) не обращается в нуль на ОДЗ для уравнения A(x)=B(x), то уравнения A(x)=B(x) и A(x)·C(x)=B(x)·C(x), как и уравнения A(x)=B(x) и A(x):C(x)=B(x):C(x) - равносильные.

Пусть q – корень уравнения A(x)=B(x). Тогда A(q)=B(q) – верное числовое равенство. Из того, что ОДЗ для выражения C(x) не уже ОДЗ для уравнения A(x)=B(x) следует, что выражение C(x) имеет смысл при x=q. Значит, C(q) – это некоторое число. Причем C(q) отлично от нуля, что следует из условия не обращения выражения C(x) в нуль. Если умножить обе части равенства A(q)=B(q) на отличное от нуля число C(q), то это даст верное числовое равенство A(q)·C(q)=B(q)·C(q), из которого следует, что q – корень уравнения A(x)·C(x)=B(x)·C(x). Если разделить обе части равенства A(q)=B(q) на отличное от нуля число C(q), то это даст верное числовое равенство A(q):C(q)=B(q):C(q), из которого следует, что q – корень уравнения A(x):C(x)=B(x):C(x).

Обратно. Пусть q - корень уравнения A(x)·C(x)=B(x)·C(x). Тогда A(q)·C(q)=B(q)·C(q) – верное числовое равенство. Заметим, что ОДЗ для уравнения A(x)·C(x)=B(x)·C(x) такая же, как ОДЗ для уравнения A(x)=B(x) (это мы обосновали в одном из предыдущих пунктов текущего списка). Так как C(x) по условию не обращается на ОДЗ для уравнения A(x)=B(x) в нуль, то C(q) – отличное от нуля число. Разделив обе части равенства A(q)·C(q)=B(q)·C(q) на отличное от нуля число C(q), получим верное числовое равенство A(q)·C(q):C(q)=B(q)·C(q):C(q) и дальше A(q)=B(q). Отсюда следует, что q – корень уравнения A(x)=B(x). Если q - корень уравнения A(x):C(x)=B(x):C(x). Тогда A(q):C(q)=B(q):C(q) – верное числовое равенство. Умножив обе части равенства A(q):C(q)=B(q):C(q) на отличное от нуля число C(q), получим верное числовое равенство A(q):C(q)·C(q)=B(q):C(q)·C(q) и дальше A(q)=B(q). Отсюда следует, что q – корень уравнения A(x)=B(x).

Утверждение доказано.

Для наглядности приведем пример проведения разобранного преобразования. Осуществим деление обеих частей уравнения x³·(x²+1)=8·(x²+1) на выражение x²+1. Это преобразование равносильное, так как выражение x²+1 не обращается в нуль на ОДЗ для исходного уравнения и ОДЗ этого выражения не уже, чем ОДЗ для исходного уравнения. В результате проведения этого преобразования получим равносильное уравнение x³·(x²+1):(x²+1)=8·(x²+1):(x²+1), которое можно дальше преобразовать к равносильному уравнению x³=8.

К началу страницы

Дата добавления: 2021-07-19; просмотров: 108; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!