Код Хаффмена является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмена.
СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ
1. Неравномерный код с разделителем
В случае неравномерного кодирования необходимо построить такую схему, при которой суммарная длительность кодов при передаче данного сообщения была бы наименьшей. Длительность сообщения будет меньше, если знакам первичного алфавита, которые встречаются в сообщении чаще, присвоить меньшие по длине коды.
Параллельно должна решаться проблема различимости кодов. Если бы код был равномерным, приемное устройство при декодировании просто отсчитывало бы заданное число элементарных сигналов и интерпретировало их в соответствии с кодовой таблицей. При использовании неравномерного кодирования возможны два подхода к обеспечению различимости кодов:
· используются комбинации элементарных сигналов, которые интерпретируются декодером как разделители;
· применяются префиксные коды.
Пусть разделителем отдельных кодов букв будет - 00 (признак конца знака), а разделителем слов - 000 (пробел). Тогда код строится по правилам:
1) коды букв не должны содержать двух и более нулей подряд в середине;
2) код буквы (кроме пробела) всегда должен начинаться с 1;
3) разделителю слов 000 всегда предшествует признак конца знака 00, при этом реализуется последовательность 00000.
В соответствии с правилами, построим кодовую таблицу для букв русского алфавита, основываясь вероятностях появления отдельных букв (табл. 1).
|
|
|
Таблица 1
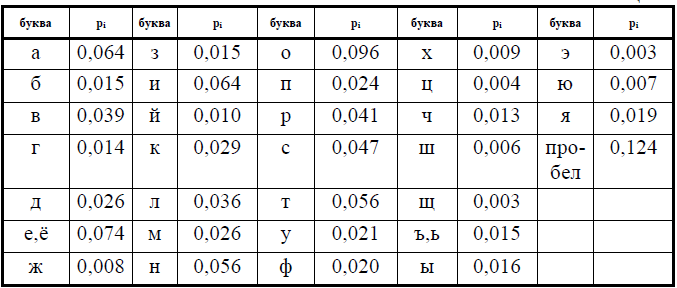
Код каждой следующей буквы получается добавлением единицы к коду предыдущей (по правилам двоичного сложения), а в ситуации, когда нарушается первое правило создания неравномерных кодов (не должно быть двух нулей в середине), запрещенный код пропускается. В таблице 2 коды букв записаны с разделителем 00 в конце.
Найдем среднюю длину кода К(r,2) для данного способа кодирования:
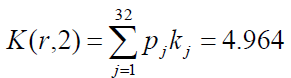
Для русского языка I(r1) = 4,356 бит, избыточность кода?
Q(r,2) = 4,964/4,356-1 = 0,14.
Это означает, что при данном способе кодирования будет передаваться на 14% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение
К(r,2) = 4,716, I(е)1 = 4,036бит, Q(e,2) =0,168.
Таблица 2
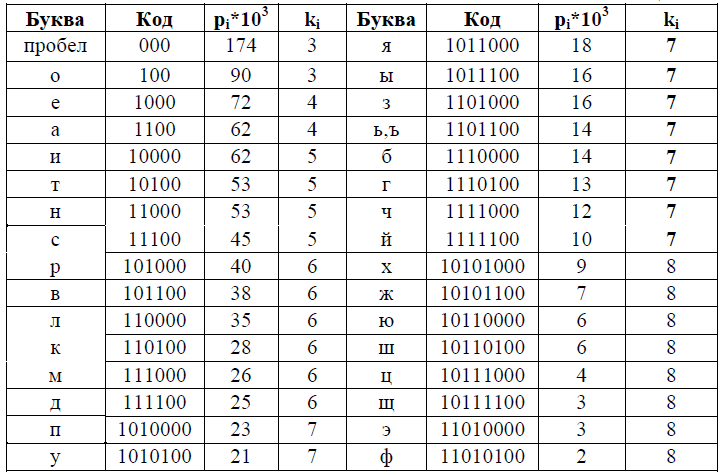
Можно дать другое, более удобное определение префиксного кода. Код называется префиксным, если он удовлетворяет условию Фано:
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом какого-либо иного, более длинного кода .
Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. При использовании префиксного кодирования не нужно передавать разделители знаков, что делает сообщение более коротким.
|
|
|
Алгоритм Хаффмена
Один из первых алгоритмов эффективного кодирования (сжатия) информации был предложен Дэвидом Хаффменом в 1952 г. задолго до появления современного цифрового компьютера (в его бытность аспирантом Массачусетского технологического института при написании курсовой работы). Обладая высокой эффективностью, алгоритм и его многочисленные адаптивные версии лежат в основе многих методов, используемых в алгоритмах кодирования. В частности, этот алгоритм стал базой для большого количества программ сжатия информации. Например, кодирование по Хаффмену используется в программах сжатия ARJ, ZIP, RAR, в алгоритме сжатия графических изображений с потерями JPEG. Коды Хэффмена дают сжатие от 20% до 90% в зависимости от типа информации.
Идея, лежащая в основе кода Хаффмена, достаточно проста. Вместо того чтобы кодировать все символы одинаковым числом бит (как это сделано, например, в ASCII кодировке, где на каждый символ отводится ровно по 8 бит), будем кодировать символы, которые встречаются чаще, меньшим числом бит, чем те, которые встречаются реже. Более того, потребуем, чтобы код был оптимален или, другими словами, минимально-избыточен.
Идея алгоритма: зная вероятность вхождения символов в сообщение, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. До начала кодирования должны быть известны вероятности появления каждой буквы, из которых будет состоять сообщение.
|
|
|
Эффективное кодирование по Хаффмену состоит в представлении наиболее вероятных (часто встречающихся) букв двоичными кодами наименьшей длины, а менее вероятных - кодами большей длины (если все кодовые слова меньшей длины уже исчерпаны). Это делается таким образом, чтобы средняя длина кода на букву исходного сообщения была минимальной. Коды Хаффмена имеют уникальный префикс, что и позволяет однозначно их декодировать, несмотря на их переменную длину. Динамический алгоритм Хаффмена на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы вероятностей строится дерево кодирования Хаффмена, с помощью которого производится кодирование букв.
Дерево - граф, обладающий следующими свойствами:
· ни в один из узлов не входит более одной дуги;
· только в один узел не входит ни одной дуги (этот узел называется корнем дерева);
· перемещаясь по дугам от корня, можно попасть в любой узел.
|
|
|
Лист дерева - узел, из которого не выходит ни одной дуги. В паре узлов дерева, соединенных между собой дугой, тот, из которого она выходит, называется родителем, другой - ребенком.
Два узла называются братьями, если имеют одного и того же родителя.
Двоичное (бинарное) дерево - дерево, у которого из всех узлов, кроме листьев, выходит ровно по две дуги.
Дерево кодирования Хаффмена - двоичное дерево, у которого каждый узел имеет вес, и при этом вес родителя равен суммарному весу его детей.
Алгоритм Хаффмена строит оптимальный префиксный код. Он основан на следующих свойствах оптимальных кодов.
1. Если код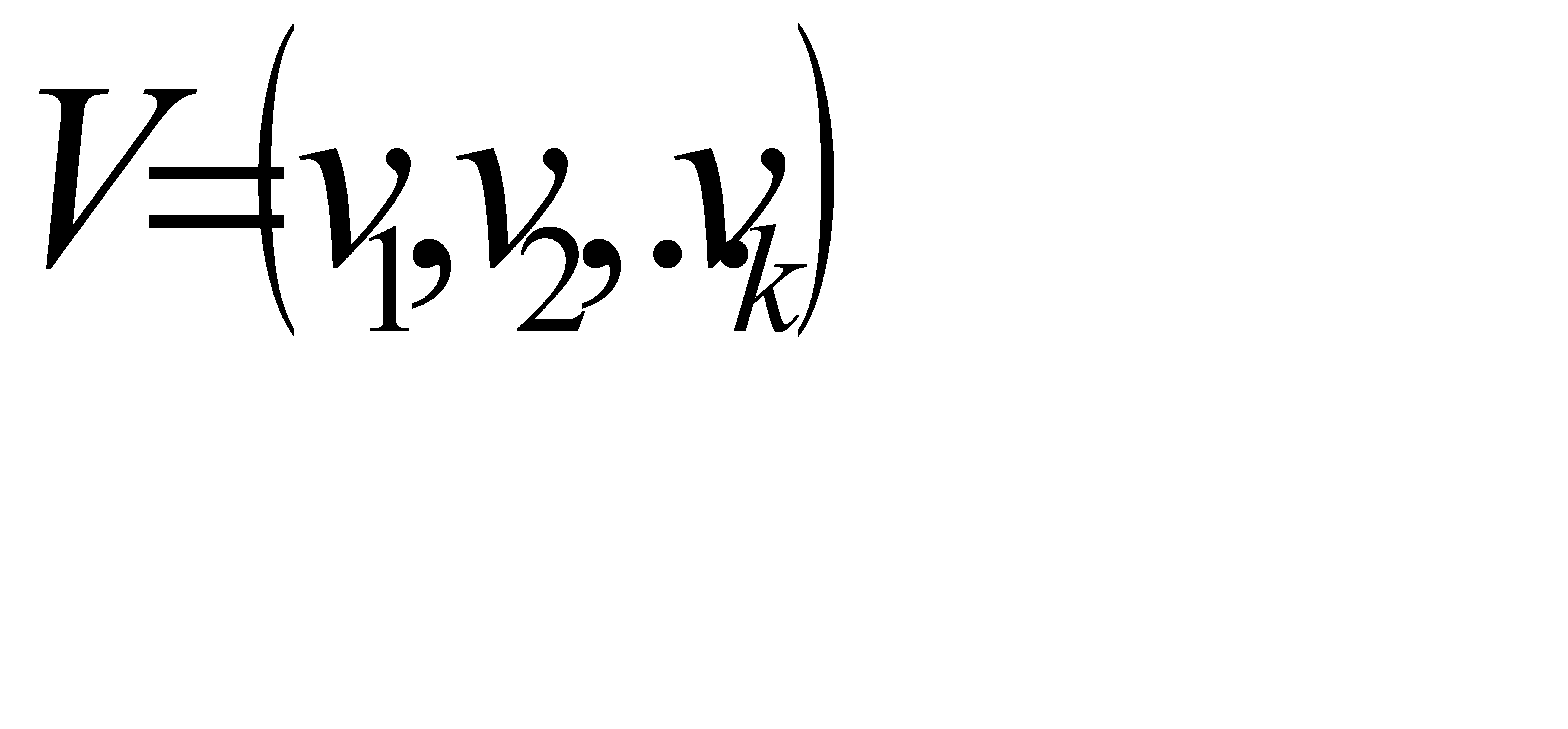 
является оптимальным для распределения вероятностей 
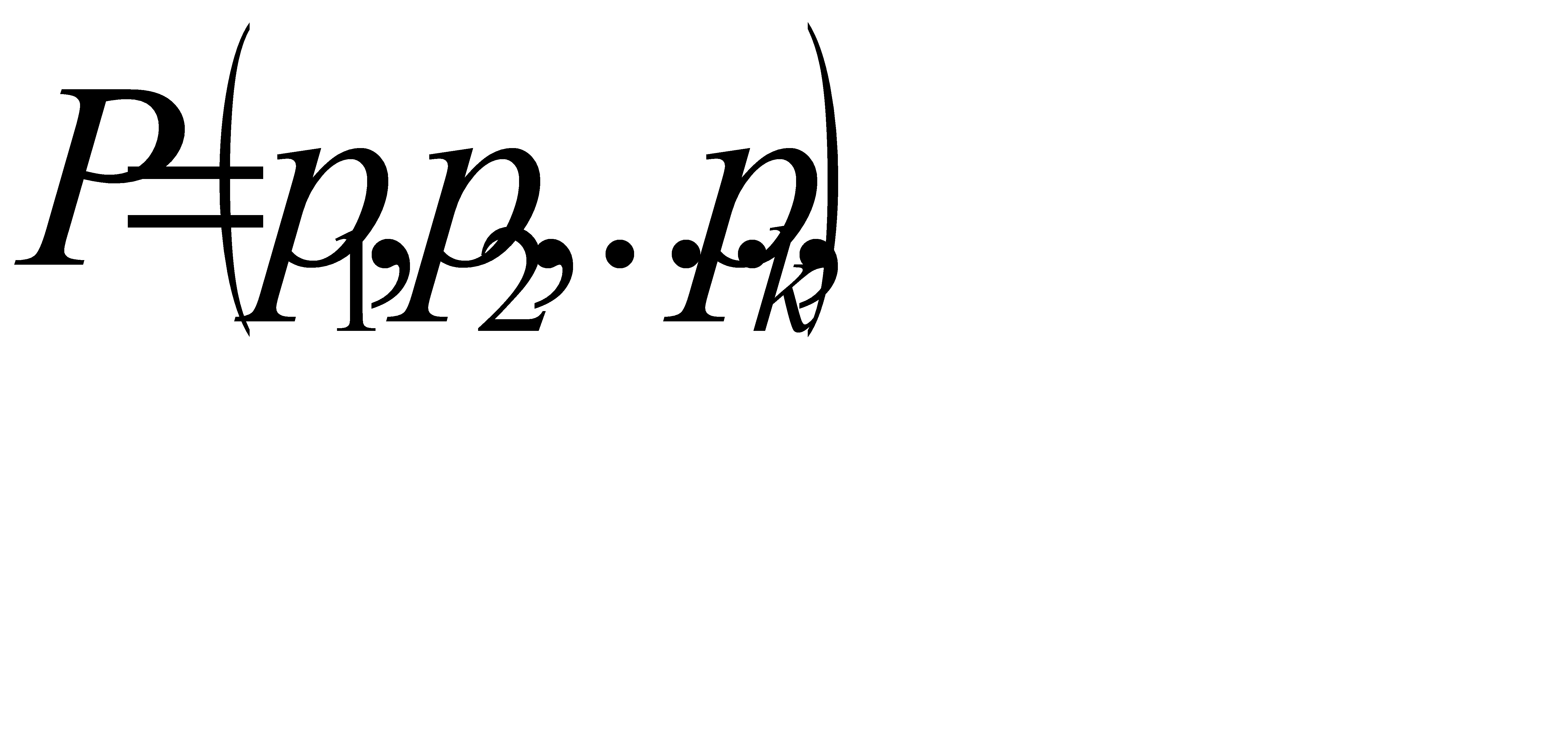, то при 
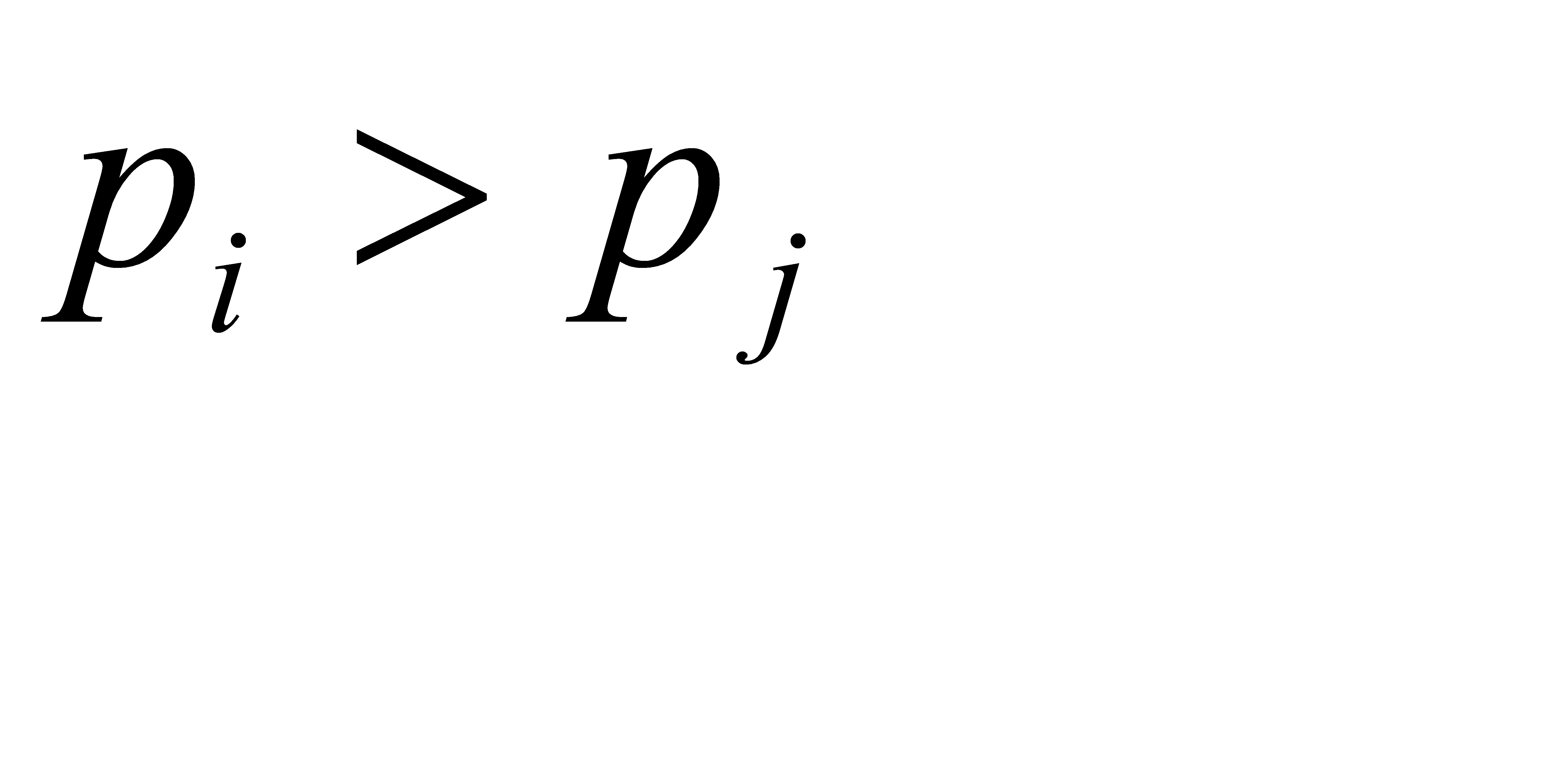выполняется условие 
.
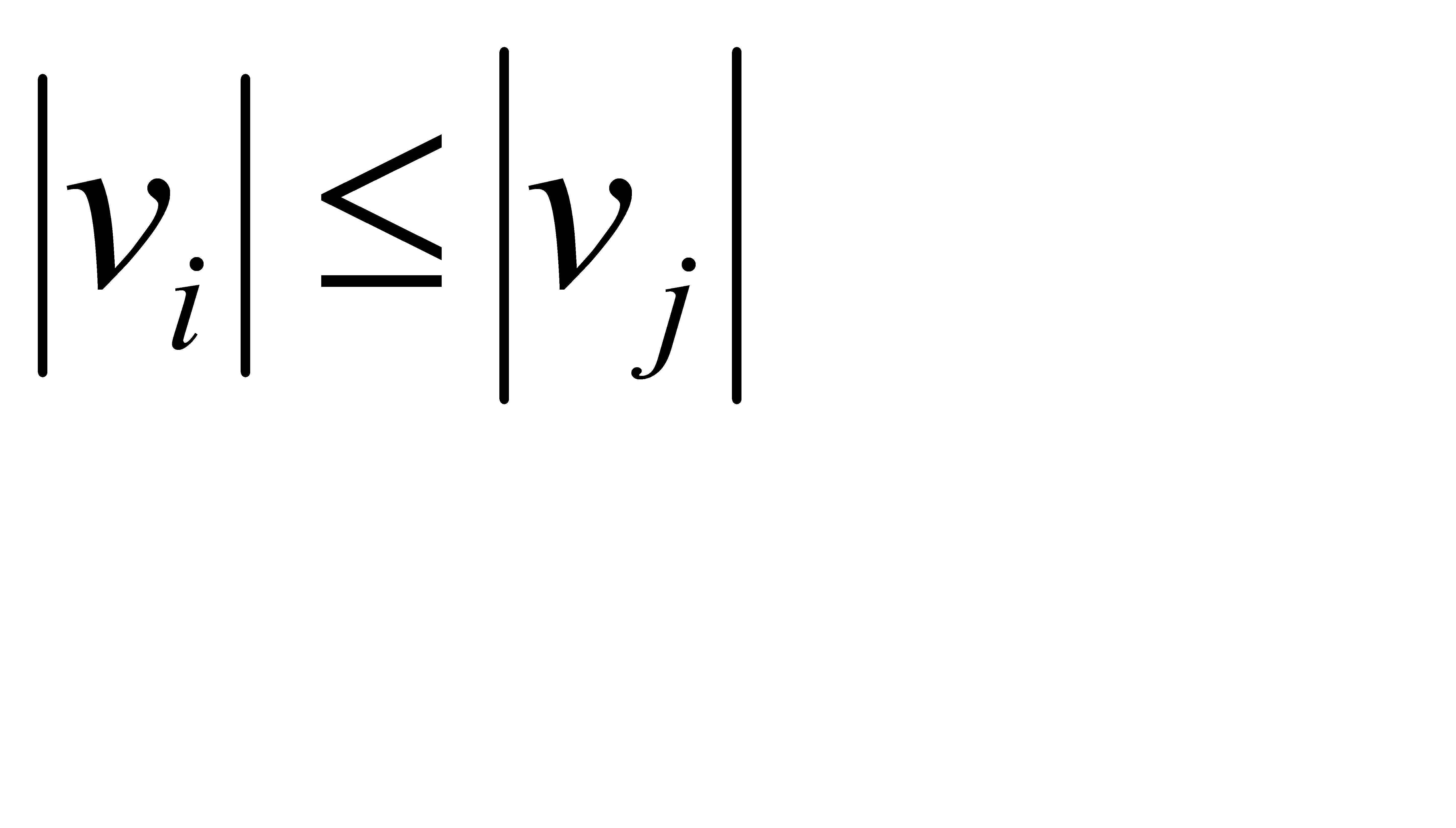Таким образом, в оптимальном кодовом дереве вероятности символов, соответствующие вершинам s-го яруса, не меньше вероятностей символов, соответствующим вершинам (s+1)-го яруса.
2. Оптимальному префиксному коду соответствует насыщенное кодовое дерево.
3. Две самые маленькие по значению вероятности в оптимальном кодовом дереве находятся на нижнем ярусе. Переставляя элементарные коды нижнего яруса, их можно расположить в вершины, для которых инцидентные им ребра будут выходить из одной вершины.
Теорема редукции . Если код с длинами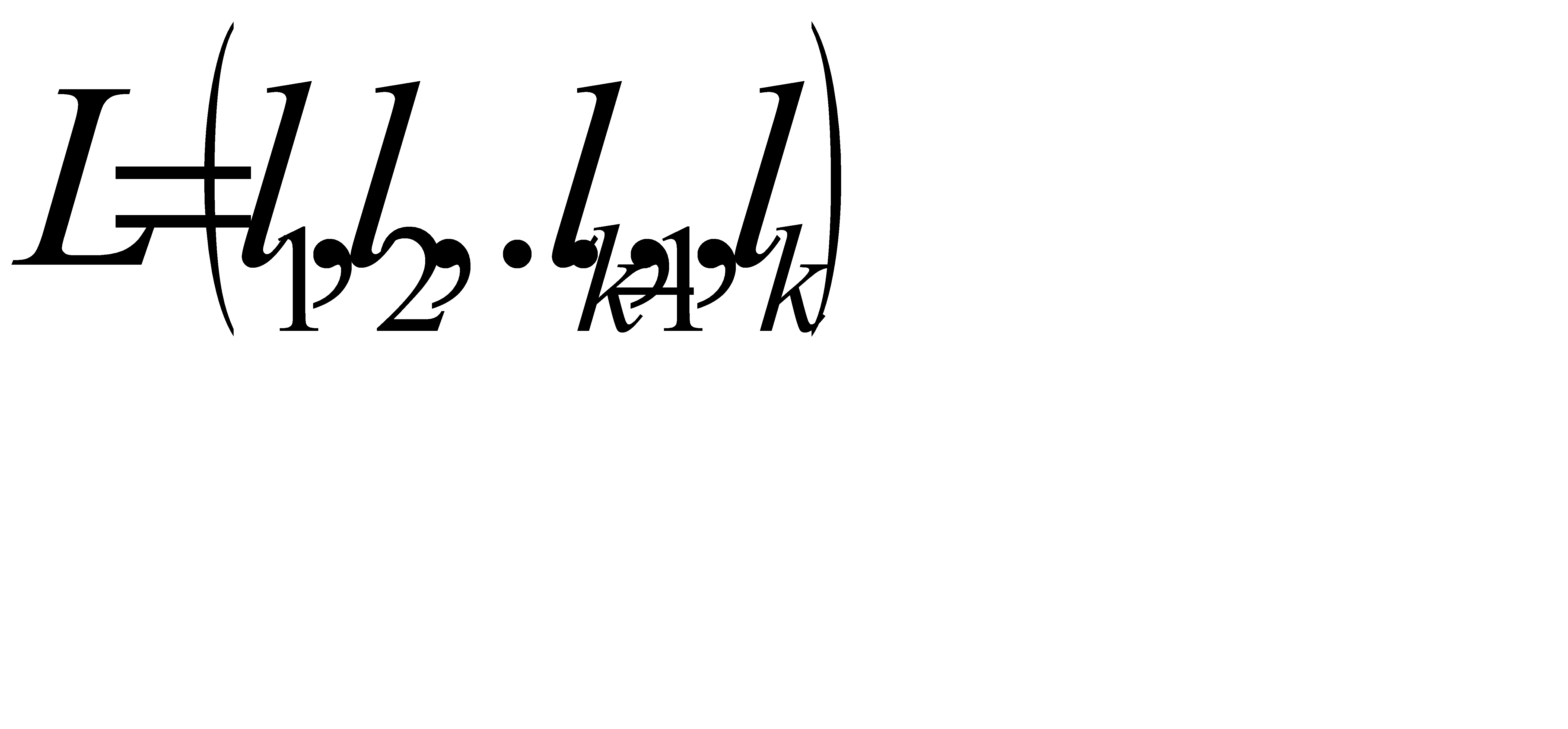 
является оптимальным для распределения вероятностей 
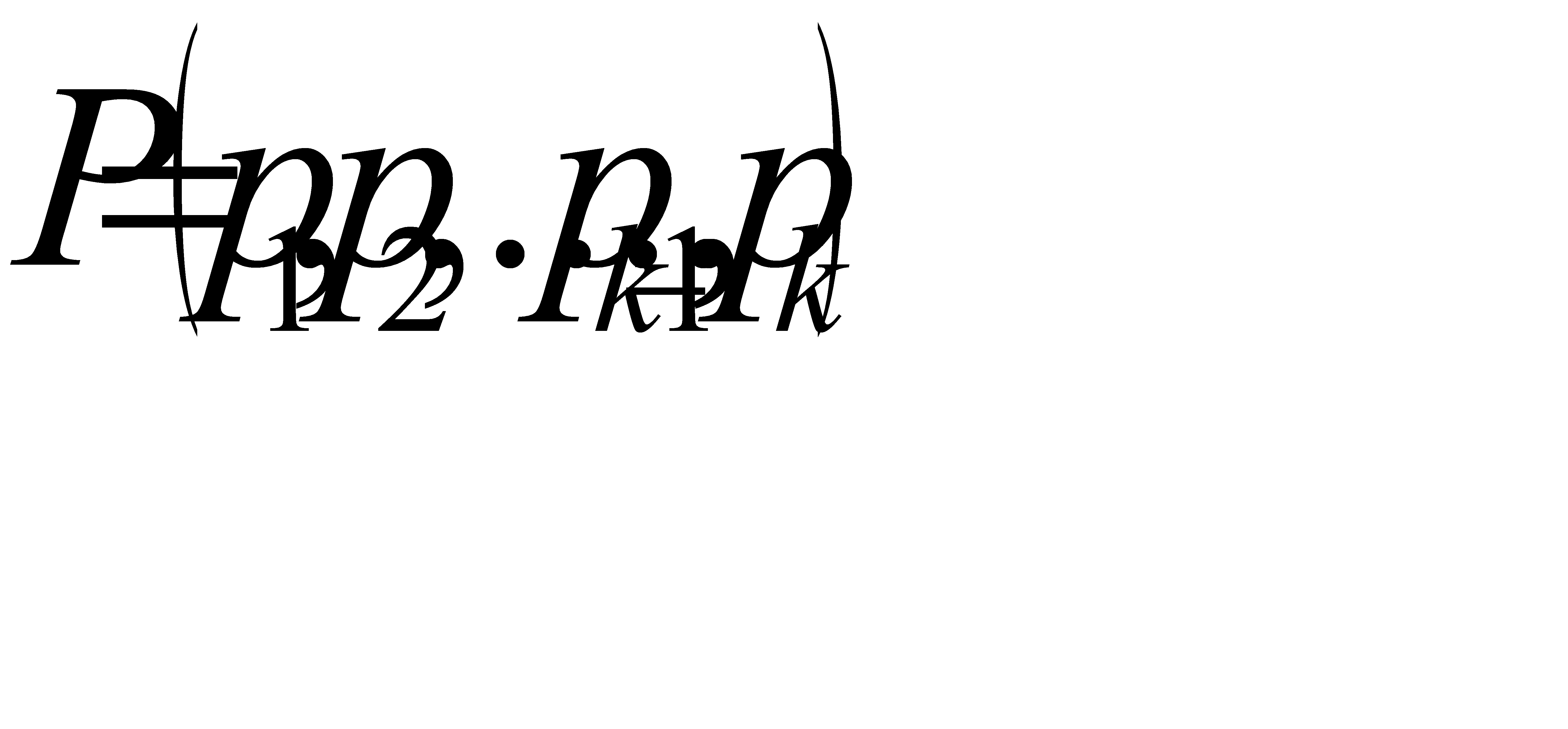, то код с длинами 
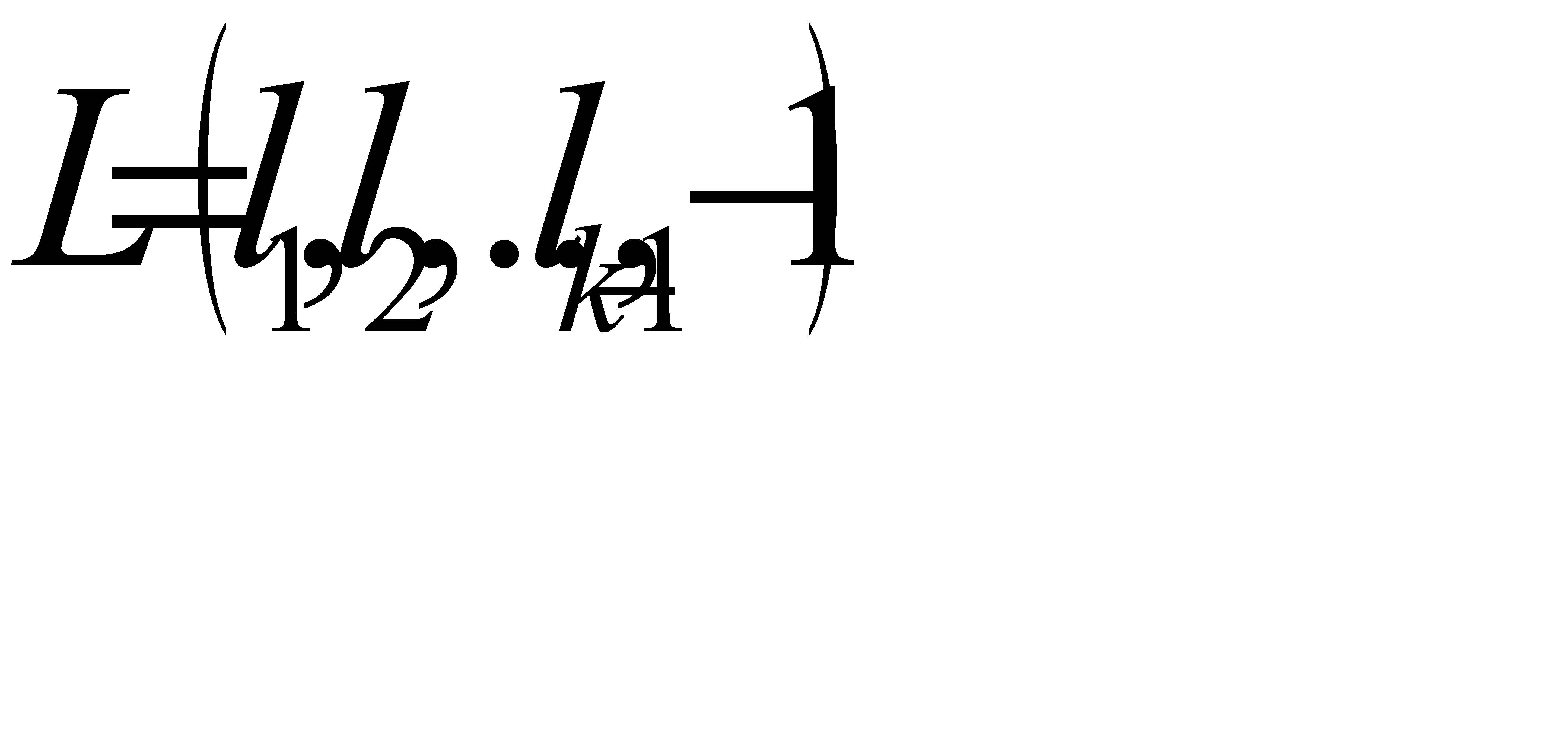является оптимальным для распределения вероятностей 
.
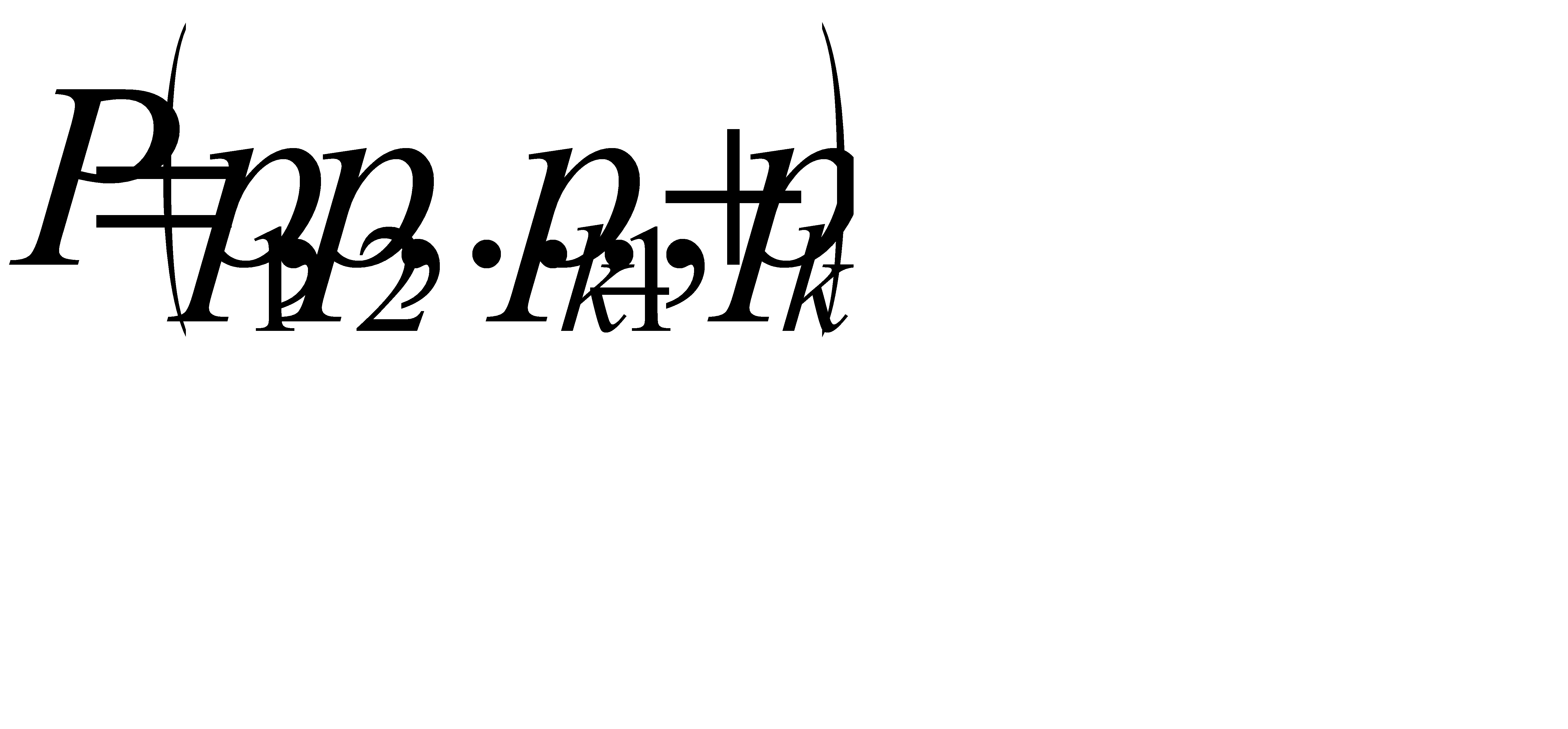Таким образом, теорема редукции позволяет свести задачу построения оптимального кода мощности k к задаче построения оптимального кода мощности k-1.
Алгоритм Хаффмена
1. Буквы входного алфавита образуют список свободных узлов будущего дерева кодирования. Каждый узел в этом списке имеет вес, равный вероятности появления соответствующей буквы в сообщении. Расположим вероятности 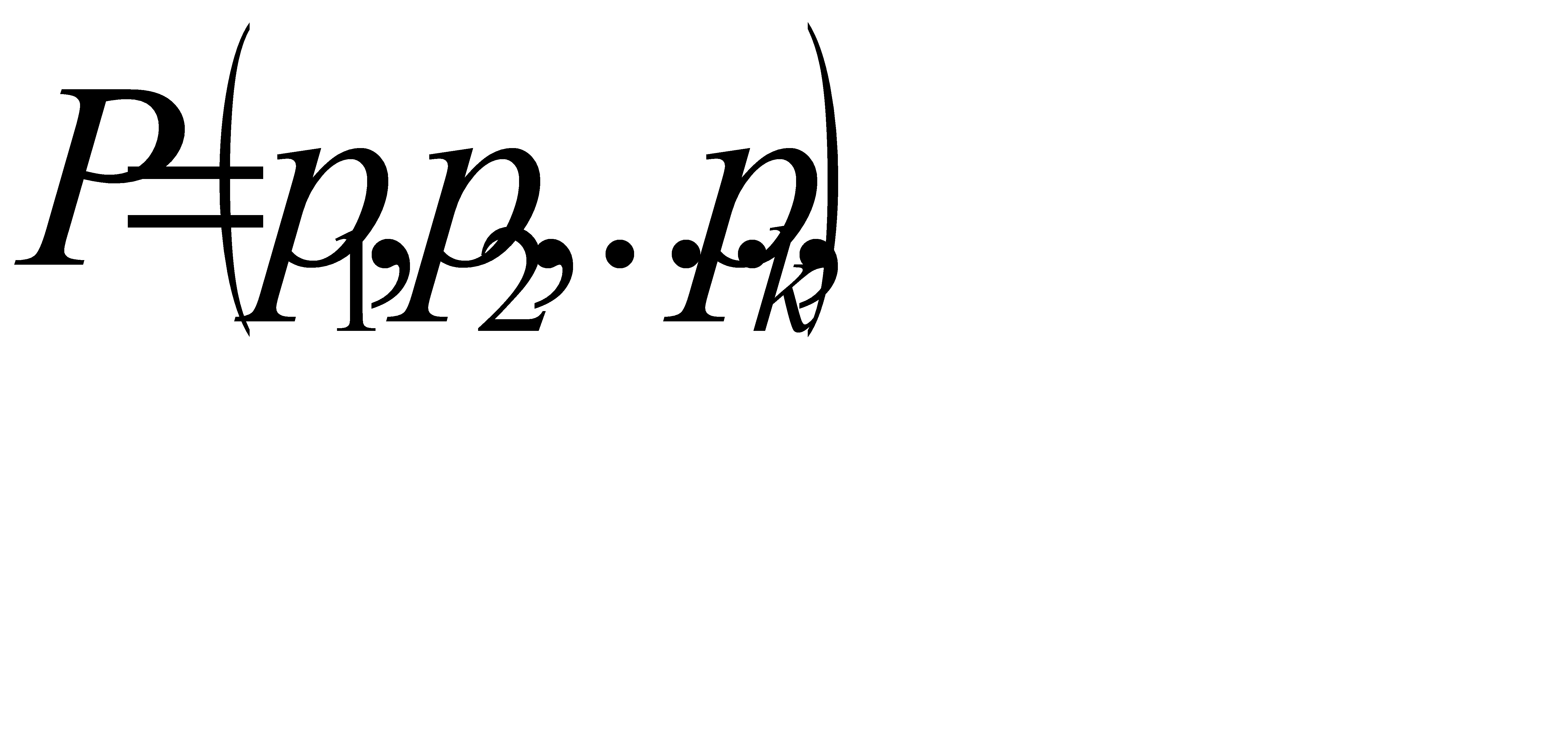в порядке невозрастания (неубывания).
2. На каждом шаге объединяем два символа, которым соответствуют наименьшие вероятности: выбираем два свободных узла дерева с наименьшими весами. Если имеется более двух свободных узлов с наименьшими весами, то можно брать любую пару. Вместо этих символов вводится новый с вероятностью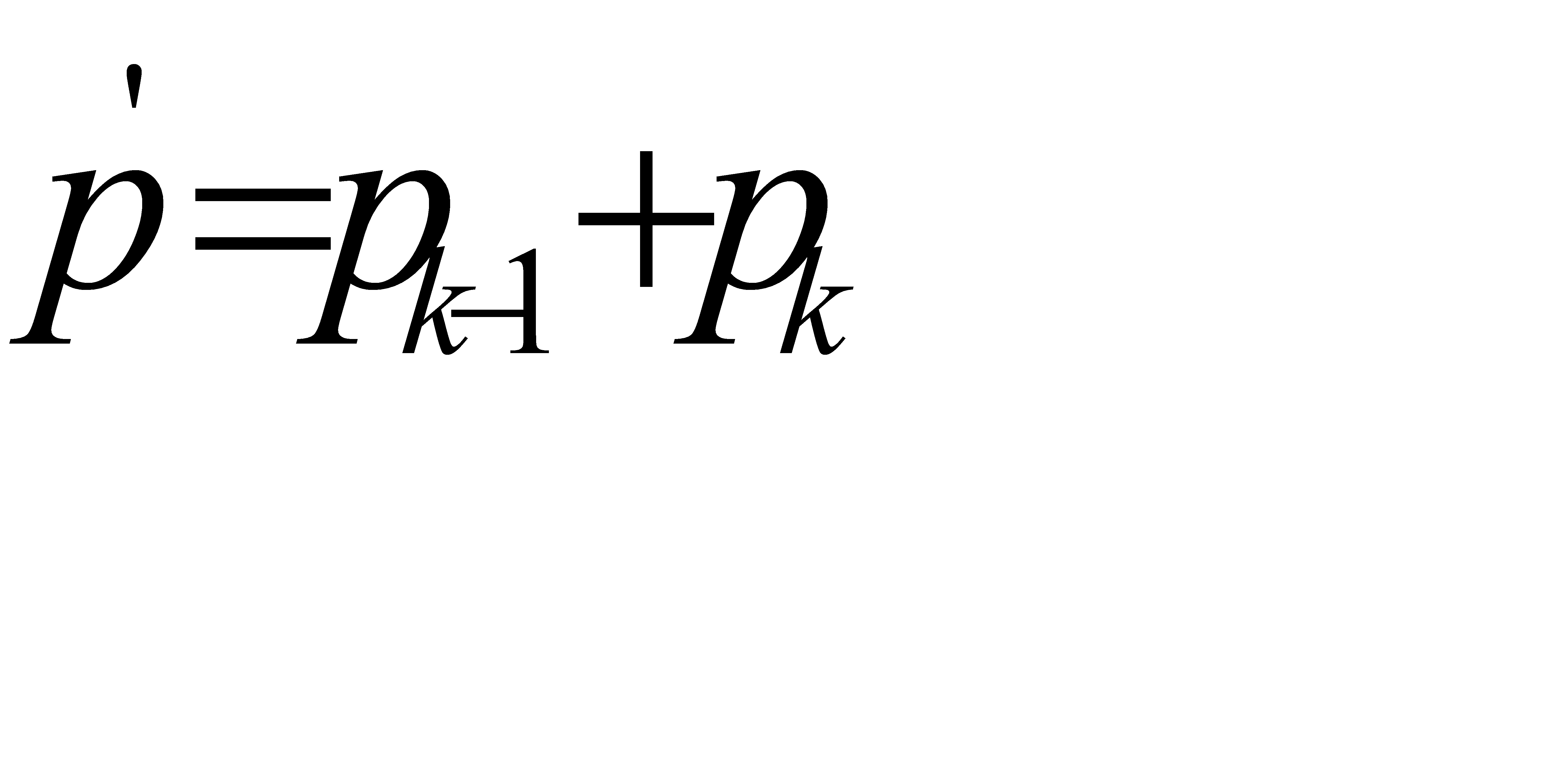 
, т.е. создается их родитель с весом, равным их суммарному весу. Вероятность 
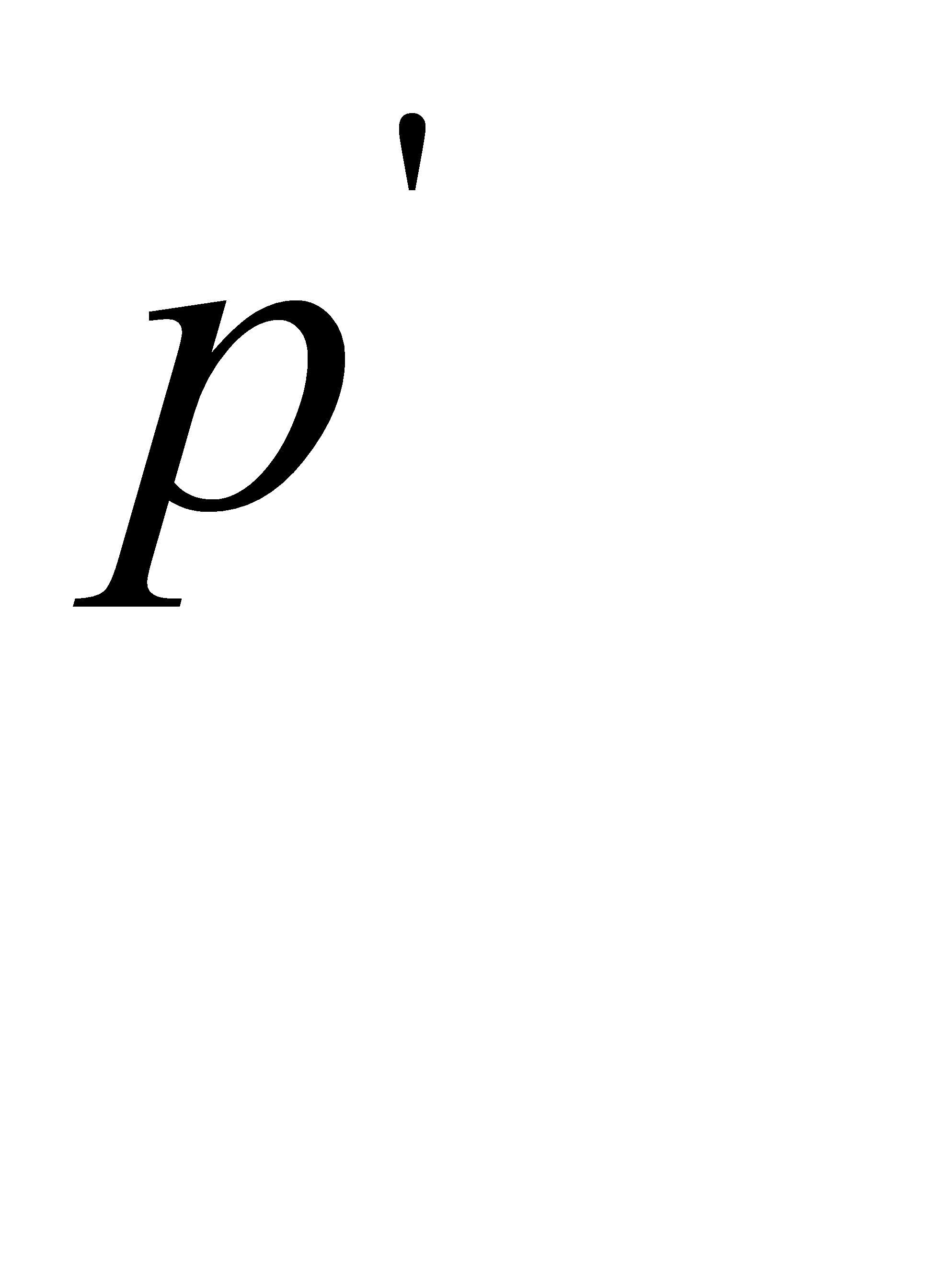вставляется в оставшийся набор вероятностей, сохраняя порядок невозрастания. Родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка. Одной дуге, выходящей из данного узла-родителя кодового дерева, ставится в соответствие значение (бит) 1, другой - 0.
3. Процесс объединения вероятностей продолжается до тех пор, пока в списке свободных узлов не останется только один. Этот узел будет являться корнем дерева. Его вес получается равным единице - суммарной вероятности всех букв сообщения.
4. Провести кодирование в обратном направлении: двум знакам последнего алфавита присвоить коды: 0 - верхнему знаку и 1 – нижнему (как в методе Шеннона-Фано). В предпоследнем алфавите, состоящем из трех знаков, одиночному знаку задать код знака последнего алфавита имеющего такую же вероятность; коды знаков, которые объединялись в один, сделать двузначными: их первой цифрой кода сделать код "родителя" – знака, имеющего объединенную вероятность, а второй цифрой: 0 для верхнего и 1 – для нижнего. Повторять до тех пор, пока не будут определены коды всех символов первичного алфавита.
Таким образом, двигаясь по кодовому дереву сверху вниз и последовательно выписывая двоичные цифры, соответствующие дугам, можно получить оптимальный код для k символов
Отметим, что алгоритм Хаффмена требует читать входной файл дважды: один раз, считая частоты вхождения символов, другой раз, производя непосредственно кодирование.
Алгоритм Хаффмена относится к жадным алгоритмам. Жадный алгоритм на каждом шаге делает локально оптимальный выбор в расчете на то, что итоговое решение также будет оптимальным. Это не всегда оправдано, но для многих задач жадные алгоритмы действительно дают оптимум.
Принцип жадного выбора . Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных (жадных) выборов дает глобально оптимальное решение. Решаемые с помощью жадных алгоритмов задачи обладают свойством оптимальности для подзадач: оптимальное решение всей задачи содержит оптимальное решение подзадач.
Различие между жадными алгоритмами и динамическим программированием можно пояснить так: на каждом шаге жадный алгоритм берет “самый жирный кусок”, а потом уже пытается сделать наилучший выбор среди оставшихся вариантов, каковы бы они ни были. Алгоритм динамического программирования принимает решение, просчитав заранее последствие всех вариантов.
Приведем несколько способов построения оптимального кода при помощи алгоритма Хаффмена.
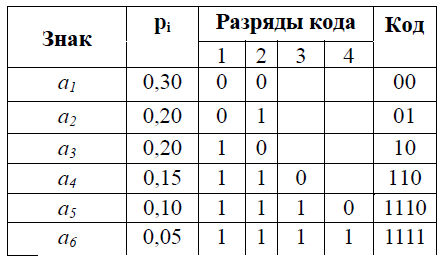
Пример. В таблице ниже построен код Шеннона-Фано для указанного распределения вероятностей алфавита из 6 символов.
Средняя длина кода:
К(А,2)=0,3×2+0,2×2+0,2×2+0,15×3+0,1×4+0,05×4=2,45 символов.
Количество информации на один знак алфавита - 2,409 бит. Избыточность кода. около 1,7%. Данный код не оптимальный, т.к. вероятности появления 0 и 1 неодинаковы (примерно 0,35 и 0,65, соответственно). Применение алгоритма кодирования Шеннона - Фано к русскому алфавиту дает избыточность кода 0,0147.
Используя алгоритм Хаффмена, построим оптимальный код для заданного алфавита.
1. Расположим знаки алфавита в порядке убывания вероятностей.
2. Создадим новый алфавит, объединив два знака с наименьшими вероятностями (а5 и а6) и заменив их одним знаком а5(1) с вероятностью,равной сумме вероятностей а5 и а6.
3. Остальные знаки включим в новый алфавит без изменения. Общее число знаков в новом алфавите будет на 1 меньше, чем в исходном.
4. Упорядочим знаки в новом алфавите по убыванию вероятностей и продолжим создавать новые алфавиты согласно п. 2 - 3, пока в последнем не останется два знака (см. таблицу).
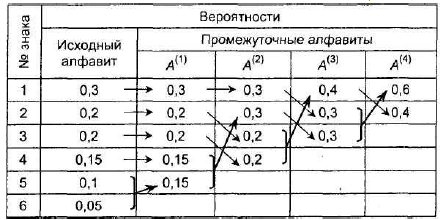
Проведем кодирование в обратном направлении. Двум знакам последнего алфавита присвоим коды 0 и 1 (верхний знак - 0, а нижний - 1). В примере знак а1(4) алфавита А(4) имеющий вероятность 0,6 получит код 0, а а2(4) c вероятностью 0,4 - код 1. В алфавите А(3) знак а1(3) получает от а2(4) его вероятность 0,4 и код 1; коды знаков а2(3) и а3(3), происходящие от знака а1(4) с вероятностью 0,6 будут уже двузначным: их первой цифрой станет код их "родителя" (0), а вторая цифра, как мы условились, у верхнего 0, у нижнего – 1. Таким образом, а2(3) будет иметь код 00, а а3(3) - код 01 и т.д. Процедура кодирования представлена в таблице ниже.
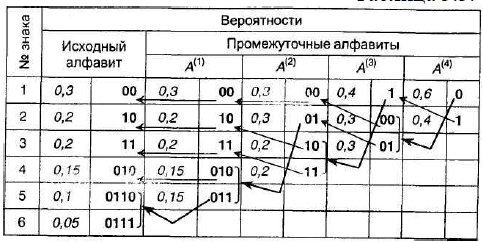
Коды удовлетворяют условию Фано, т.е. являются префиксными, и, следовательно, не требуют разделителя. Средняя длина кода:
К(А,2) = 0,3×2 + 0,2×2 + 0,2×2 +0,15×3 + 0,1×4 + 0,05×4 = 2,45.Избыточность - 0,017, однако, вероятности 0 и 1 сблизились (0,47 и 0,53, соответственно). Первичный алфавит очень короткий, и полученные коды во многом похожи, характеристики кода Хаффмена совпали с характеристиками кода Шеннона-Фано.
Более высокая эффективность кодов Хаффмена, по сравнению с кодами Шеннона – Фано, становится очевидной, если сравнить избыточности кодов для естественного языка. Применение описанного алгоритма для букв русского алфавита порождает коды, представленные в таблице.
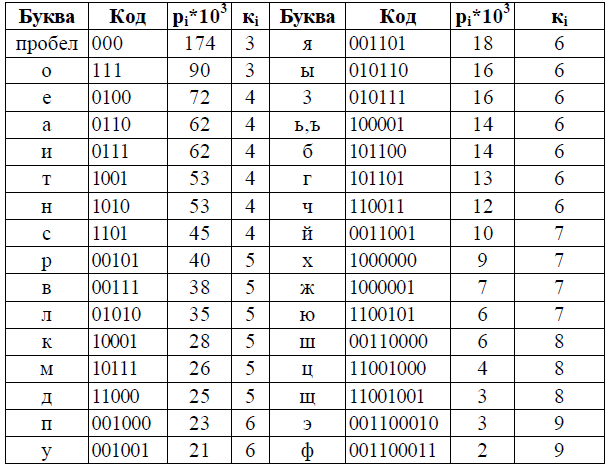
Средняя длина кода оказывается равной К(r,2) = 4,395; избыточность кода - 0,0090, т.е. не превышает 1%, что меньше избыточности кода Шеннона-Фано.
Код Хаффмена является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмена.
Код Хаффмена широко применяется в алгоритмах, используемых программами-архиваторами, программами резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах.
Пример. Построить оптимальный код, используя алгоритм Хаффмена, для алфавита, приведенного в таблице 1.
| Таблица 1 | ||||||||||||||||||
|
Построение дерева начинаем со списка листьев (см. рис. 1) и выполняем по шагам.
Рис. 1. Список свободных узлов-листьев
На 1-м шаге выбираются два листа дерева с наименьшими весами z7 и z8. Они присоединяются к узлу-родителю, вес которого равен 0,04+0,02=0,06. Затем узлы z7 и z8 удаляются из списка свободных. Узел z7 соответствует ветви 0 родителя, узел z8 - ветви 1.
На 2-м шаге "наилегчайшей" парой оказывается лист z6 и свободный узел (z7+z8). Для них создается родитель с весом 0.16. Узел z6 соответствует ветви 0 родителя, узел (z7+z8) - ветви 1.
На 3-м шаге наименьшие вероятности имеют z5, z4, z3 и свободный узел (z6+z7+z8). Таким образом, на данном шаге можно создать родителя для z5 и (z6+z7+z8) с весом 0.26.
В данной ситуации возможны несколько вариантов соединения узлов с наименьшими весами. При этом все такие варианты будут правильными, хотя и могут привести к различным наборам кодов, которые, впрочем, будут обладать одинаковой эффективностью для заданного распределения вероятностей.
На 4-м шаге "наилегчайшей" парой оказываются листья z3 и z4.
На 5-м шаге выбираем узлы с наименьшими весами 0.22 и 0.20.
На 6-м шаге остается три свободных узла с весами 0.42, 0.32 и 0.26. Выбираем наименьшие веса 0.32 и 0.26.
На 7-м шаге остается объединить две оставшиеся свободные вершины, после чего получаем окончательное дерево кодирования Хаффмена, приведенное на рис. 1.
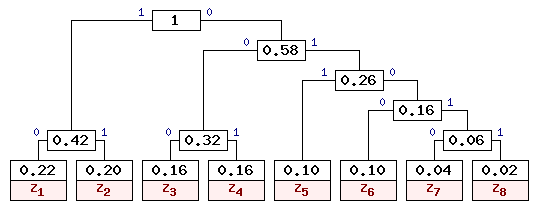
Рис. 1. Дерево кодирования Хаффмена
На основании построенного дерева символы представляются кодами, отражающими путь от корневого узла до листа, соответствующего нужному символу. В рассмотренном примере символы входного алфавита кодируются так, как показано в таблице 2.
| Таблица 2 | ||||||||||||||||||
|
Очевидно, что наиболее вероятные буквы закодированы самыми короткими кодами, а наиболее редкие - кодами большей длины. Причем коды построены таким образом, что ни одна кодовая комбинация не совпадает с началом более длинной комбинации. Это позволяет однозначно декодировать сообщения без использования разделительных символов.
Для заданных в таблице 1 вероятностей можно построить и другие правильные варианты кодового дерева Хаффмена. Одно из допустимых деревьев приведено на рис. 2. Коды букв входного алфавита для данного кодового дерева приведены в таблице 3.
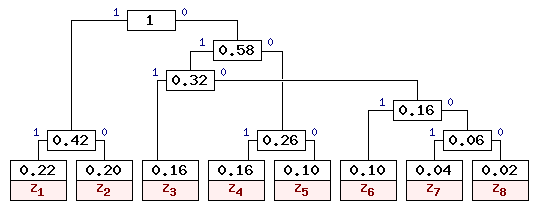
Рис. 2. Альтернативный вариант дерева кодирования Хаффмена
| Таблица 3 | ||||||||||||||||||
|
Из таблицы 3 видно, что коды также получились префиксными, и наиболее вероятным буквам соответствуют наиболее короткие коды.
Пример. Построить оптимальный код, используя алгоритм Хаффмена, для алфавита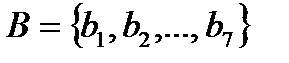 
с заданным распределением вероятностей 
.
Процесс построения оптимального кода можно представить несколько иначе. Расположим вероятности в порядке невозрастания. На каждом шаге объединяем два символа с наименьшими вероятностями. Вместо этих символов вводится новый с вероятностью 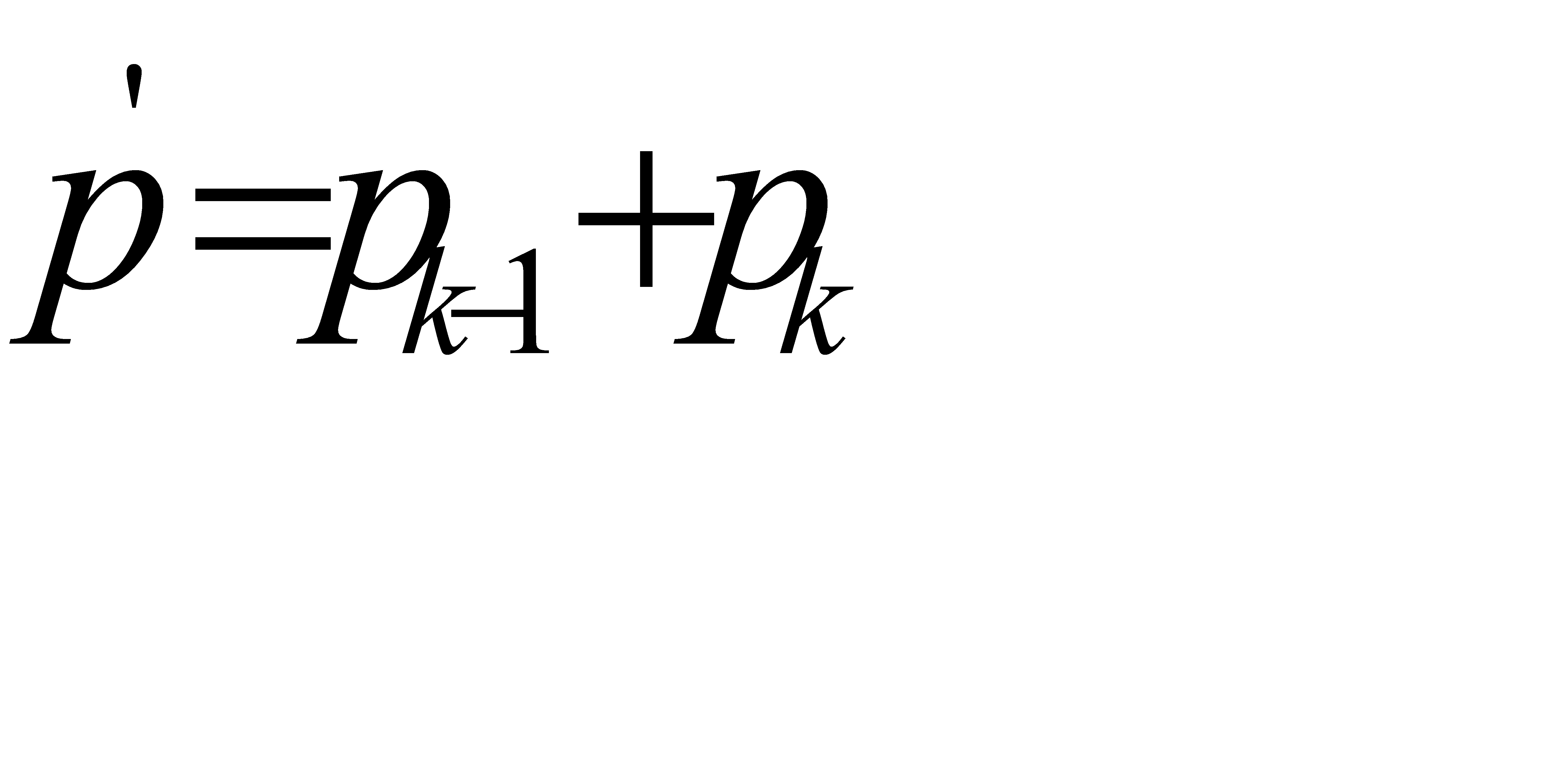. Вероятность 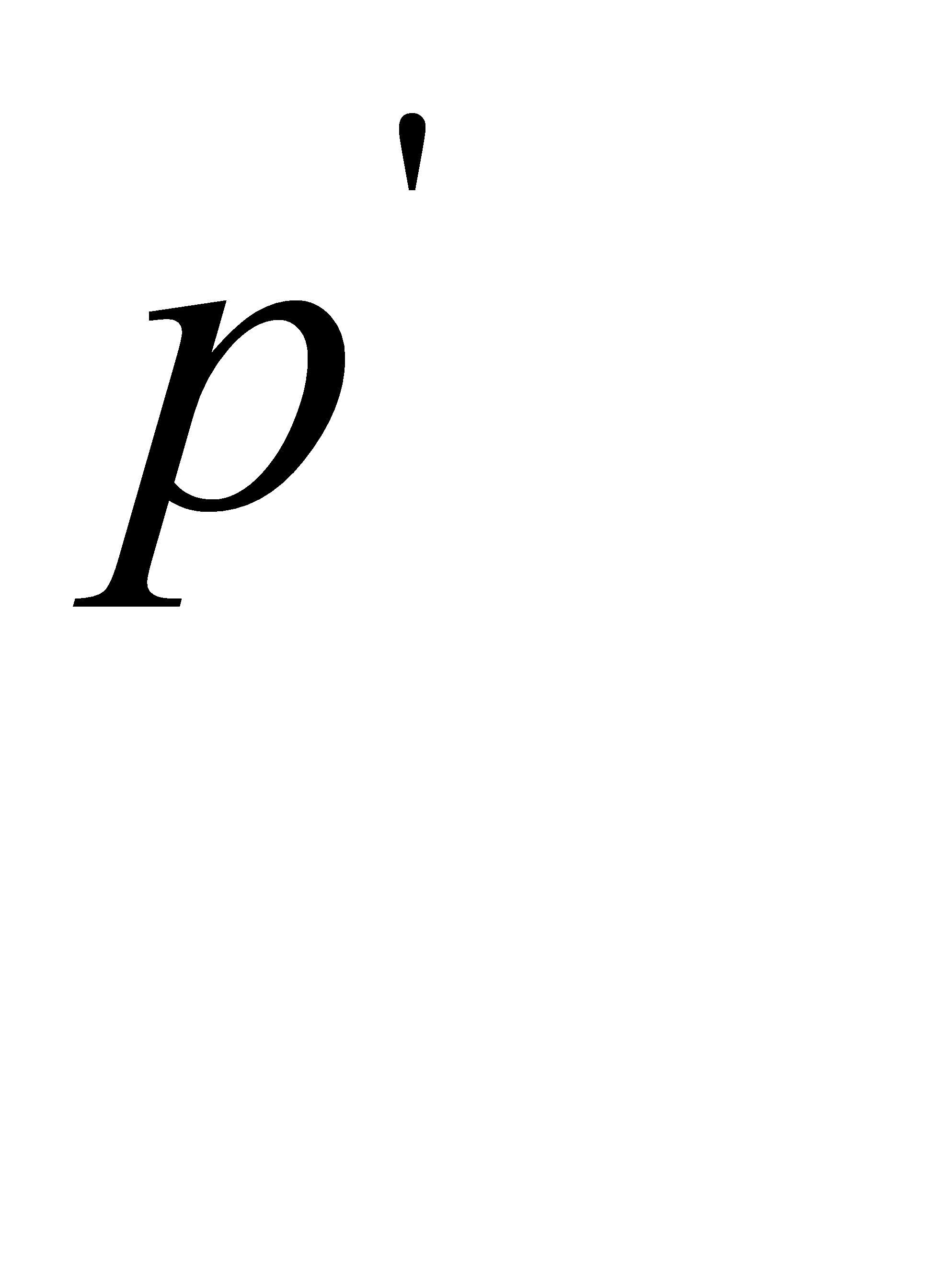вставляется в оставшийся набор вероятностей, сохраняя их порядок невозрастания.
Здесь фигурными скобками обозначены объединяемые вероятности. Затем осуществляем движение в обратном порядке к вероятностям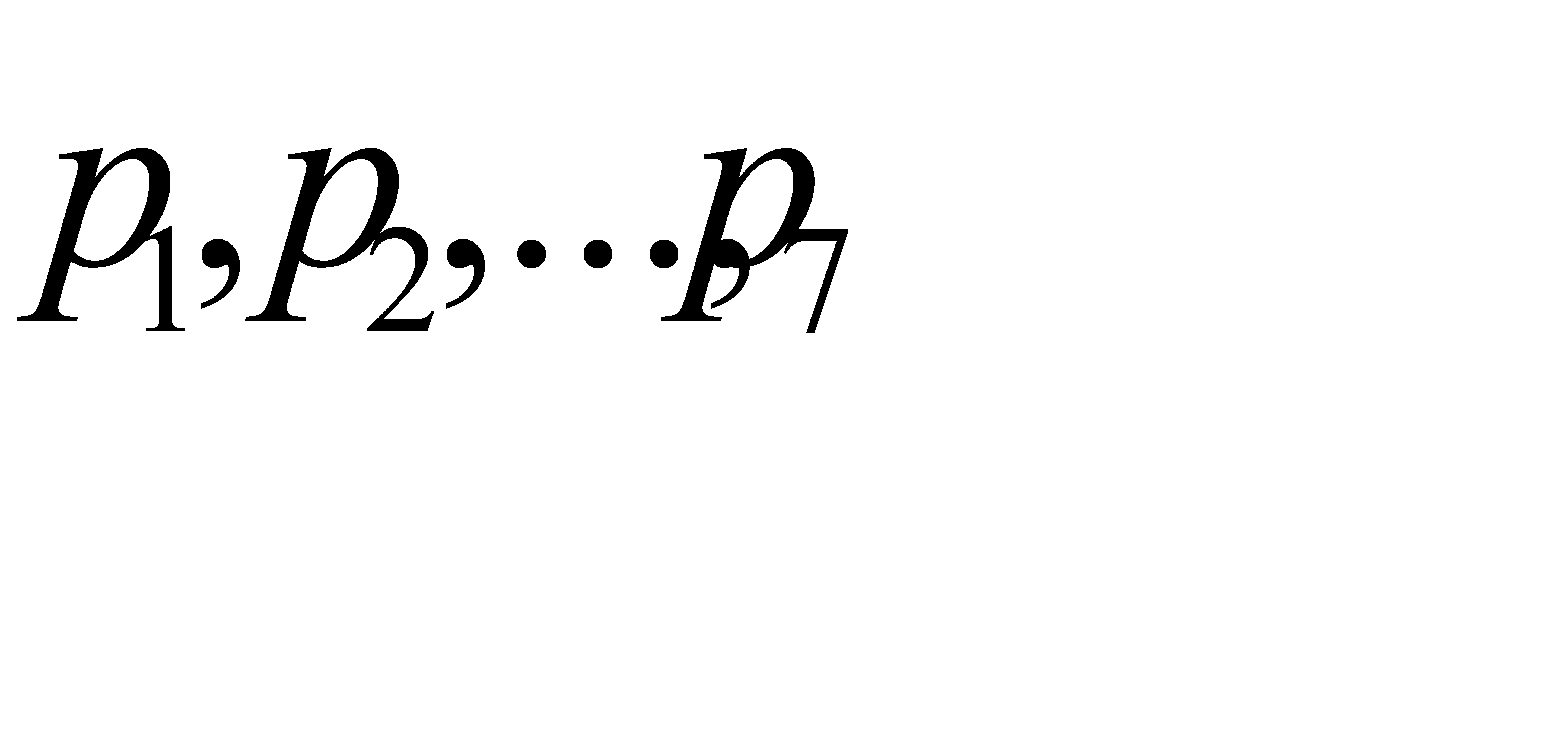 
, проходя соответствующие скобки, выписываем элементарные коды символов алфавита:
Например, путь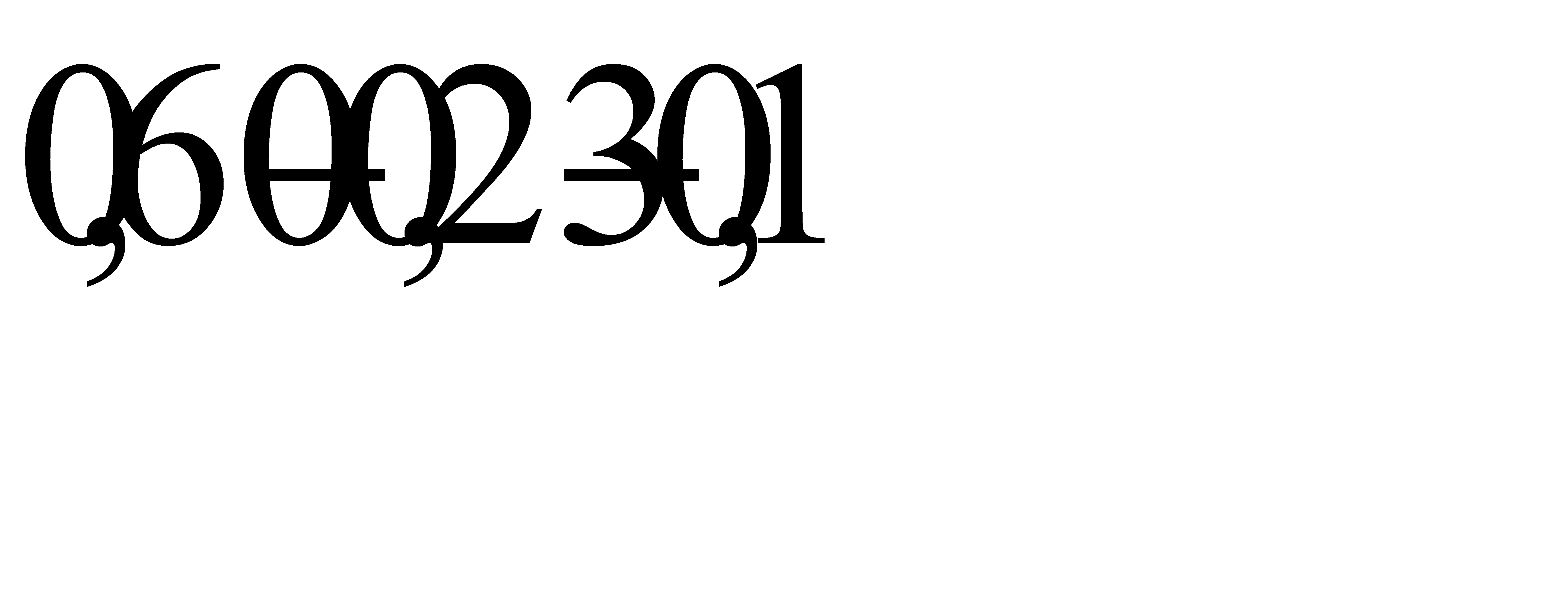 
дает элементарный код 
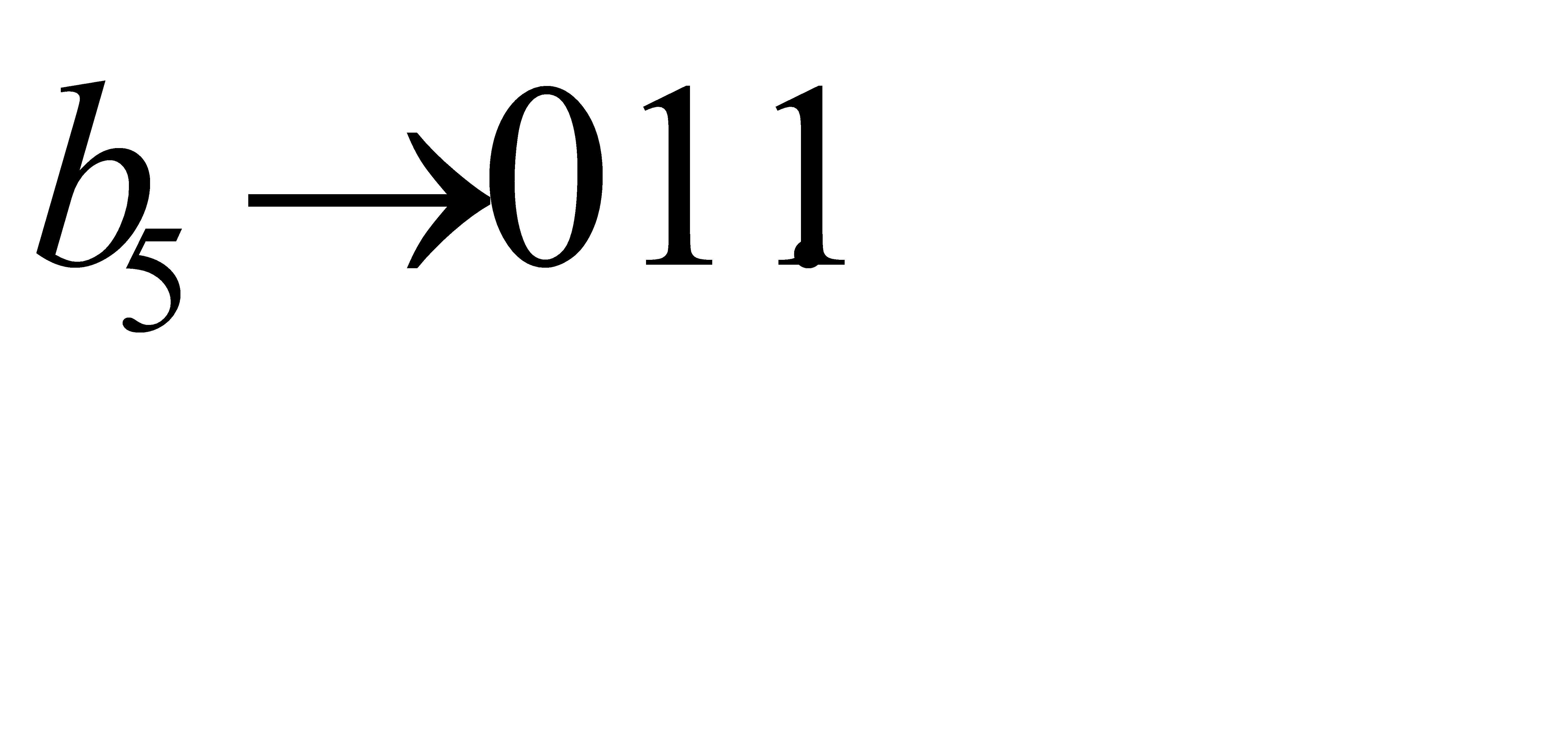Очевидно, что стоимость данного способа кодирования равна
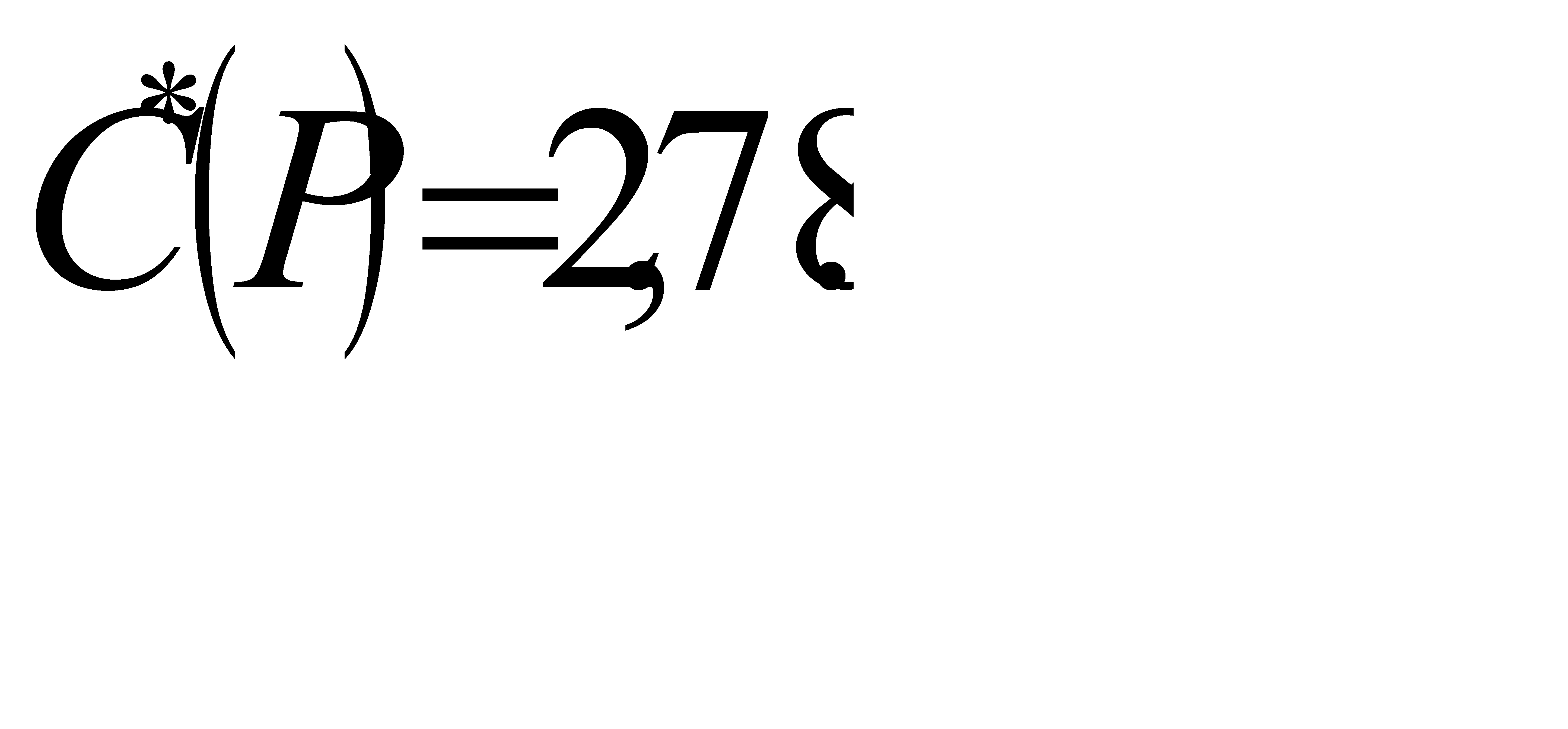
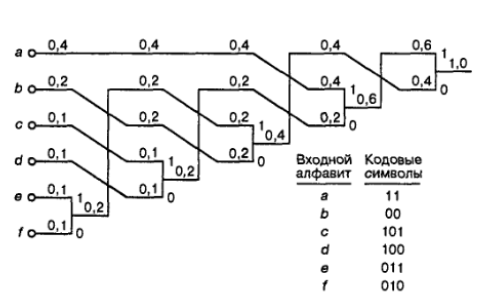
Пример. Рассмотрим другую методику построения кода Хаффмена для 6-символьного алфавита:
Пример. Построить оптимальный код для алфавита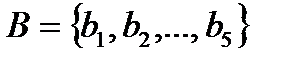 
с заданным распределением вероятностей 
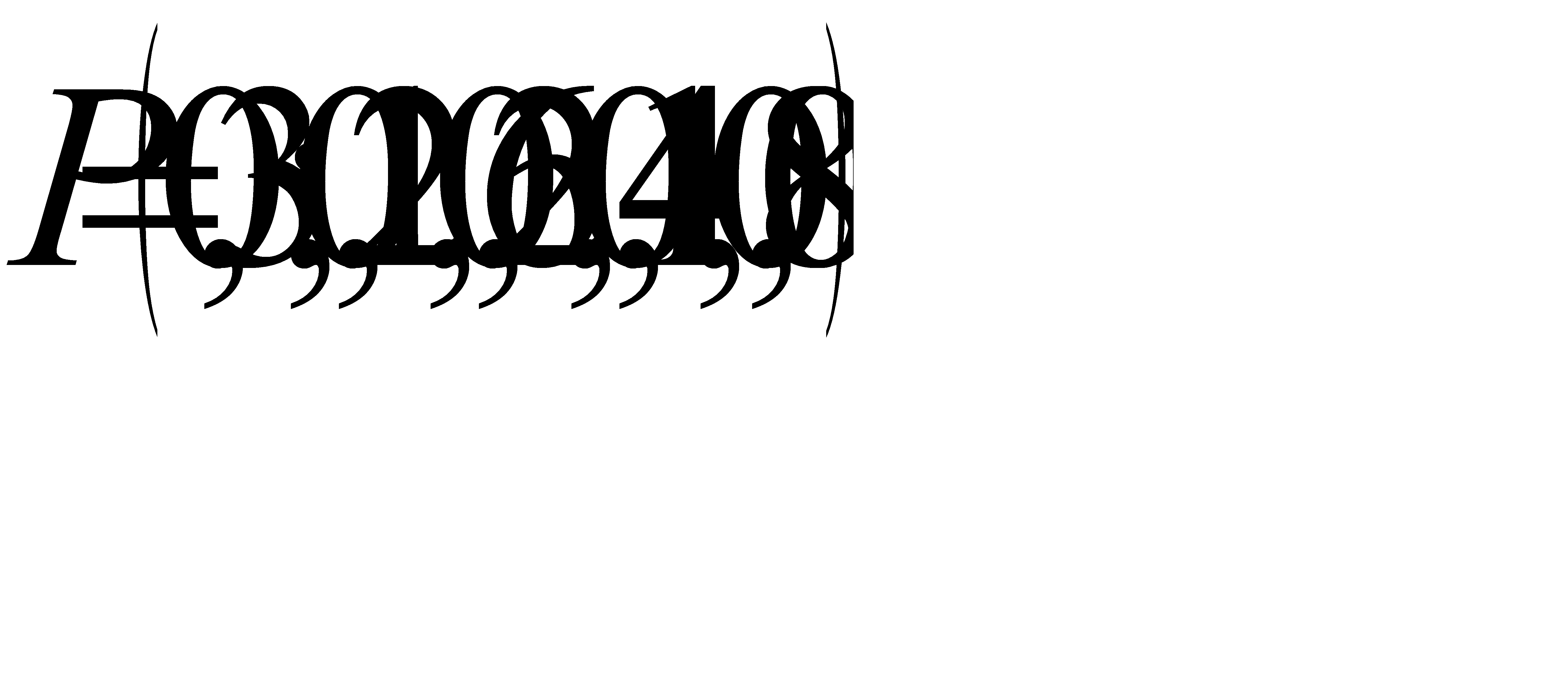, используя алгоритмом Хаффмена. Найти стоимость кода.
Согласно алгоритму, суммируем последовательно каждые две наименьшие вероятности, результирующая сумма вставляется в оставшийся набор вероятностей, сохраняя порядок невозрастания. Вся процедура преобразований представлена в таблице. Суммируемые элементы выделены жирным шрифтом.
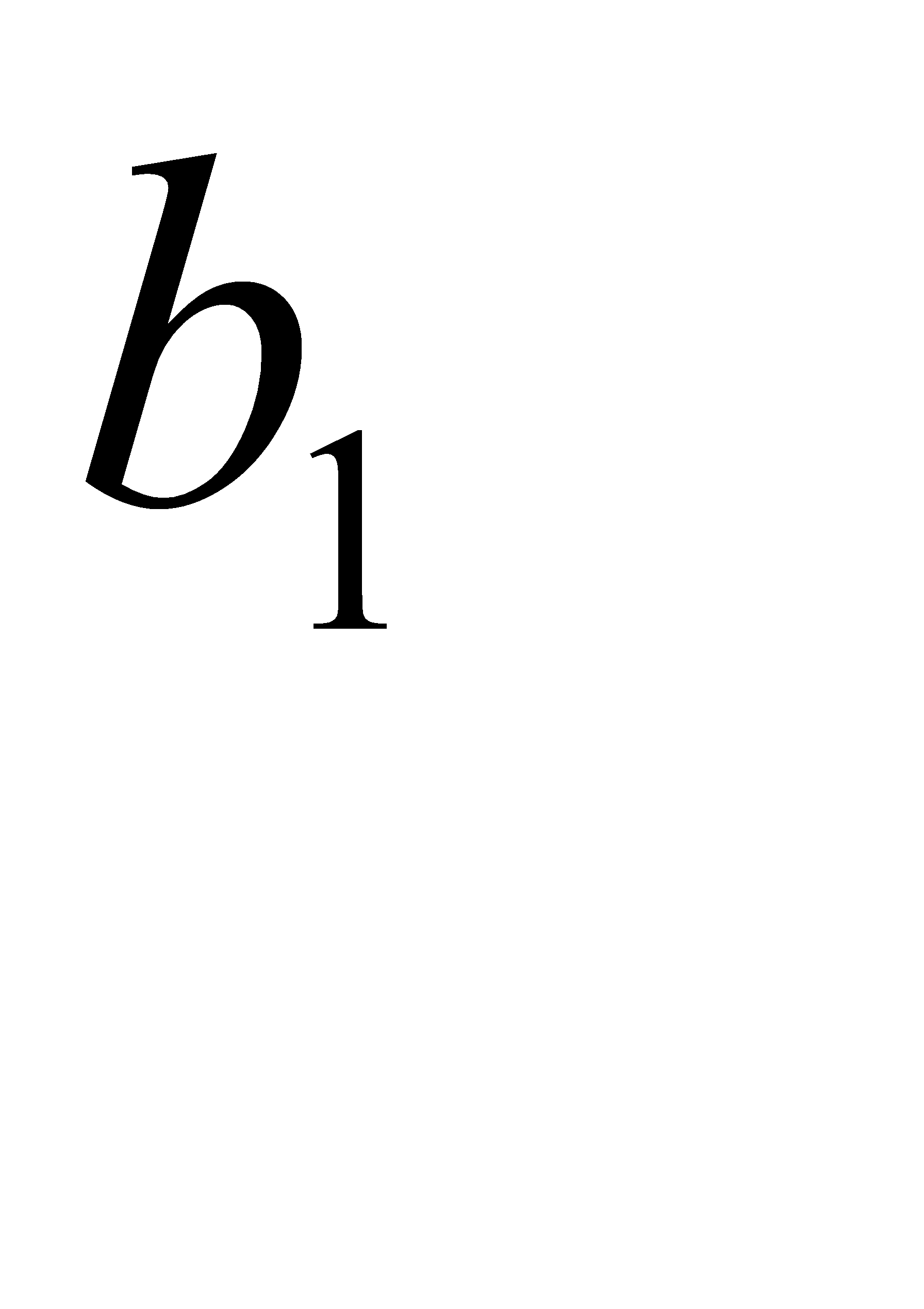
| 0,31 | 0,31 | 0,43 | 0,57 | 0 | 1 | 00 | 00 | |
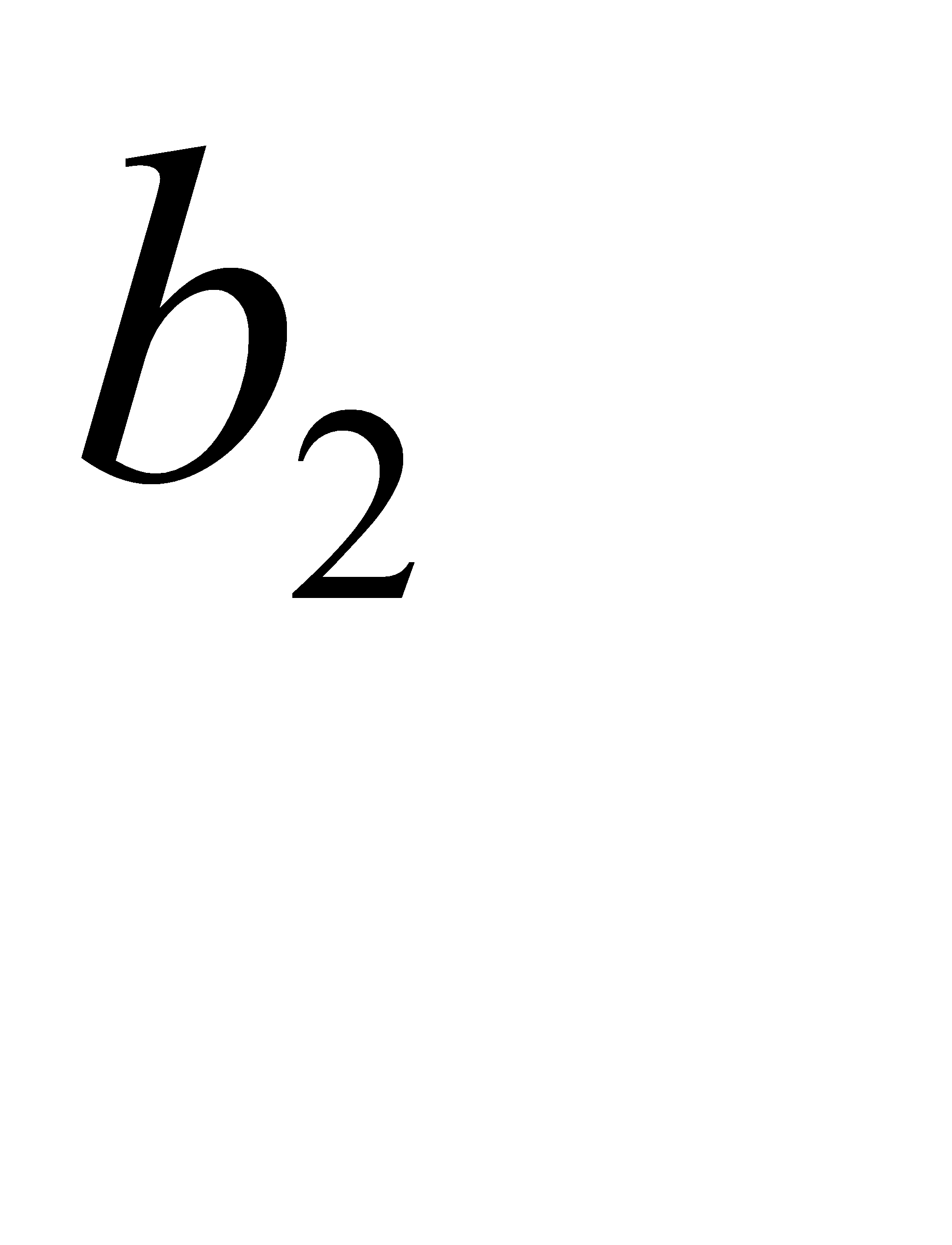
| 0,26 | 0,26 | 0,31 | 0,43 | 1 | 00 | 01 | 01 | |
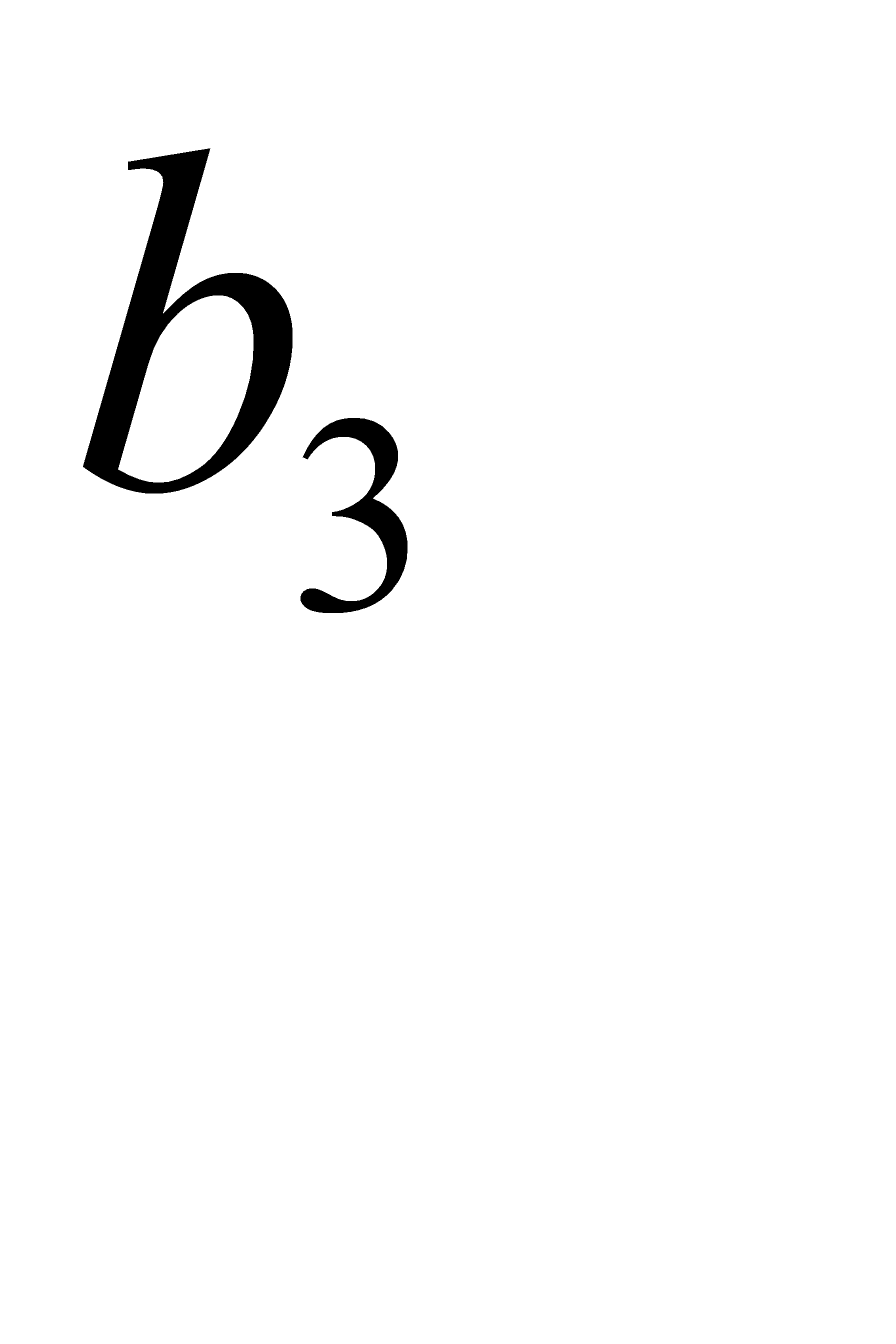
| 0,24 | 0,24 | 0,26 | 01 | 10 | 10 | |||
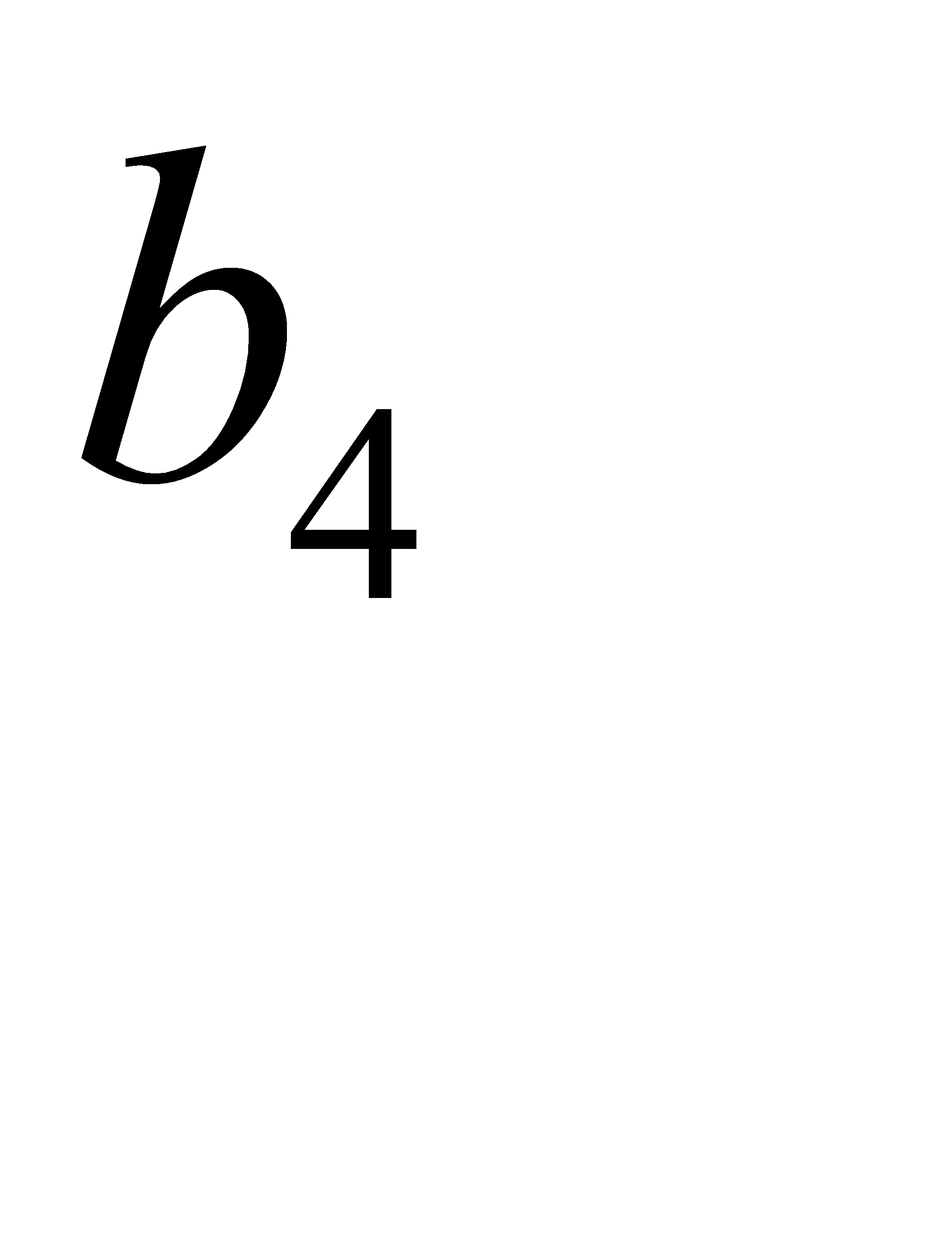
| 0,18 | 0,19 | 11 | 110 | |||||
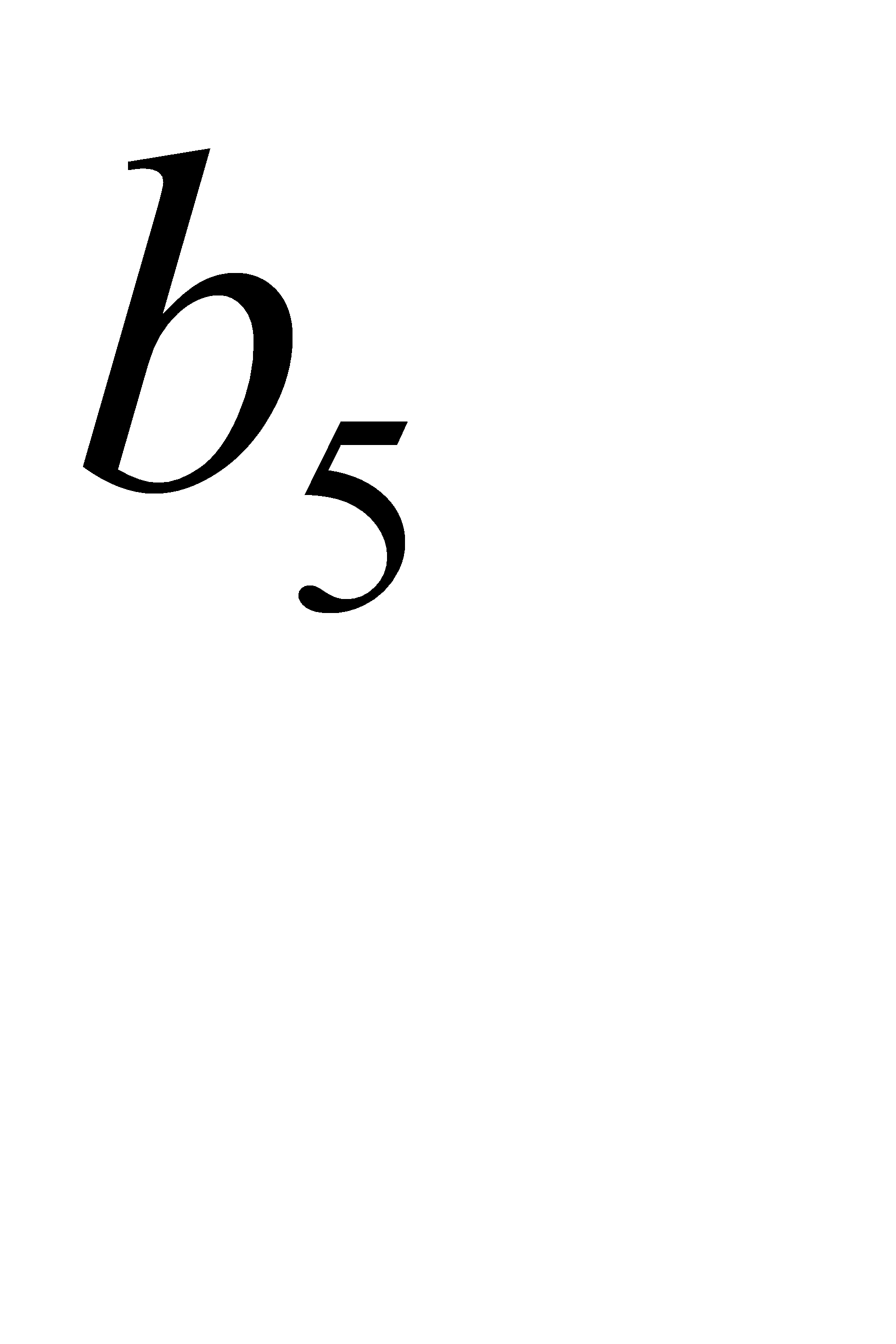
| 0,01 | 111 |
Процесс кодирования начинается с того, что оставшимся двум элементам 0,57 и 0,43 присваиваем коды 0 и 1 соответственно. Затем возвращаемся на шаг назад, элементу таблицы 0,43 оставляем такой же код 1 и, учитывая, что 0,57= 0,31+0,26 присваиваем элементам 0,31 и 0,25 код суммы 0,57, дописывая справа к нему 0 и 1 соответственно. Продолжаем кодирование аналогичным образом дальше: элементам 0,31 и 0,26 оставляем такие же коды с предыдущего этапа. Учитывая, что 0,43= 0,24+0,29 присваиваем элементам 0,24 и 0,19 код суммы 0,43, т.е. 1, дописывая справа к нему 0 и 1 соответственно.
Стоимость кодирования:
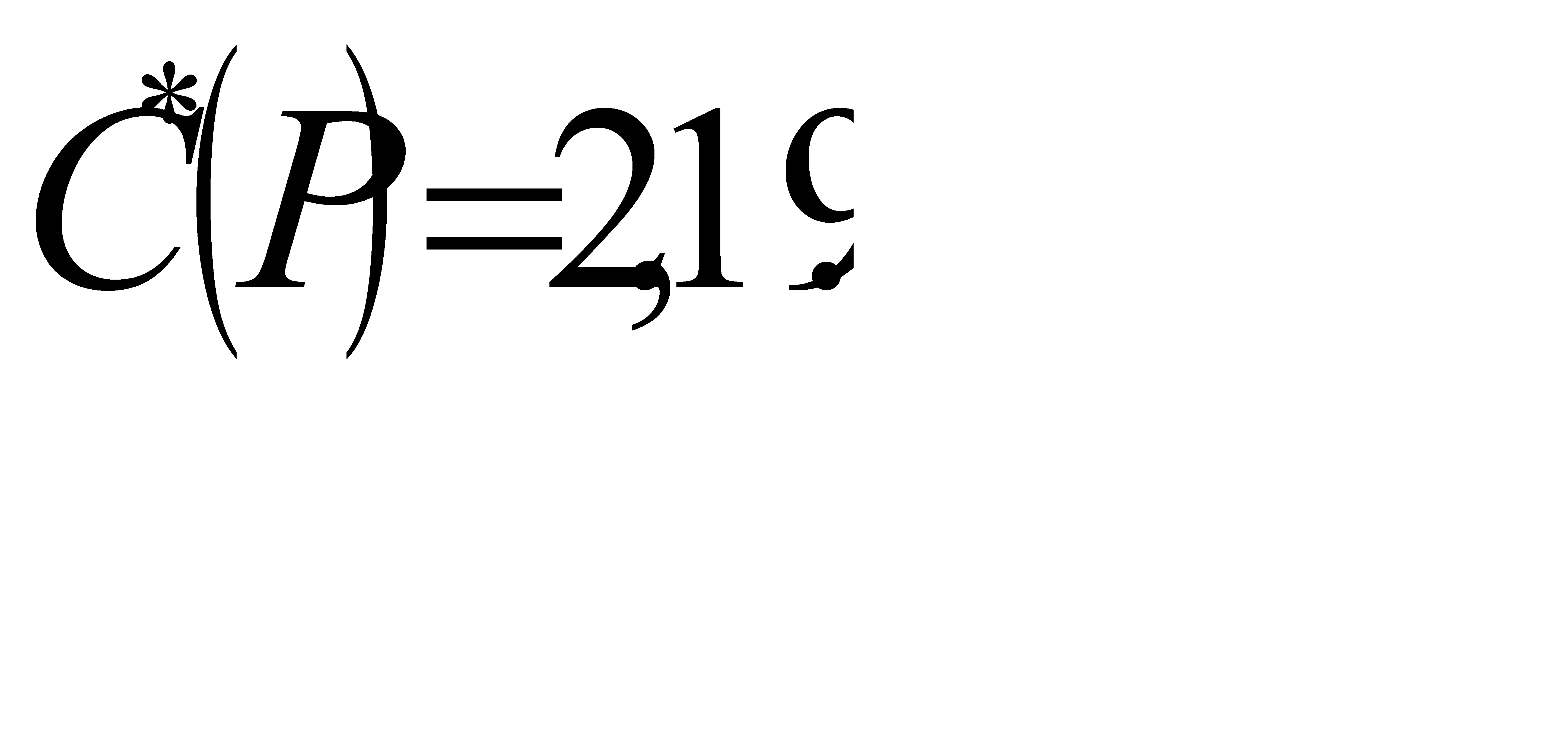
Пример. Построить оптимальный код для алфавита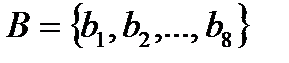 
с заданным распределением вероятностей 
, используя алгоритмом Хаффмена. Найти стоимость кода.
Аналогично предыдущему примеру, в таблице ниже приведена процедура объединения вероятностей и построения кода. Напомним, что левая часть таблицы соответствует объединения вероятностей. Правая часть таблицы соответствует построению префиксного кода с минимальной избыточностью.
|
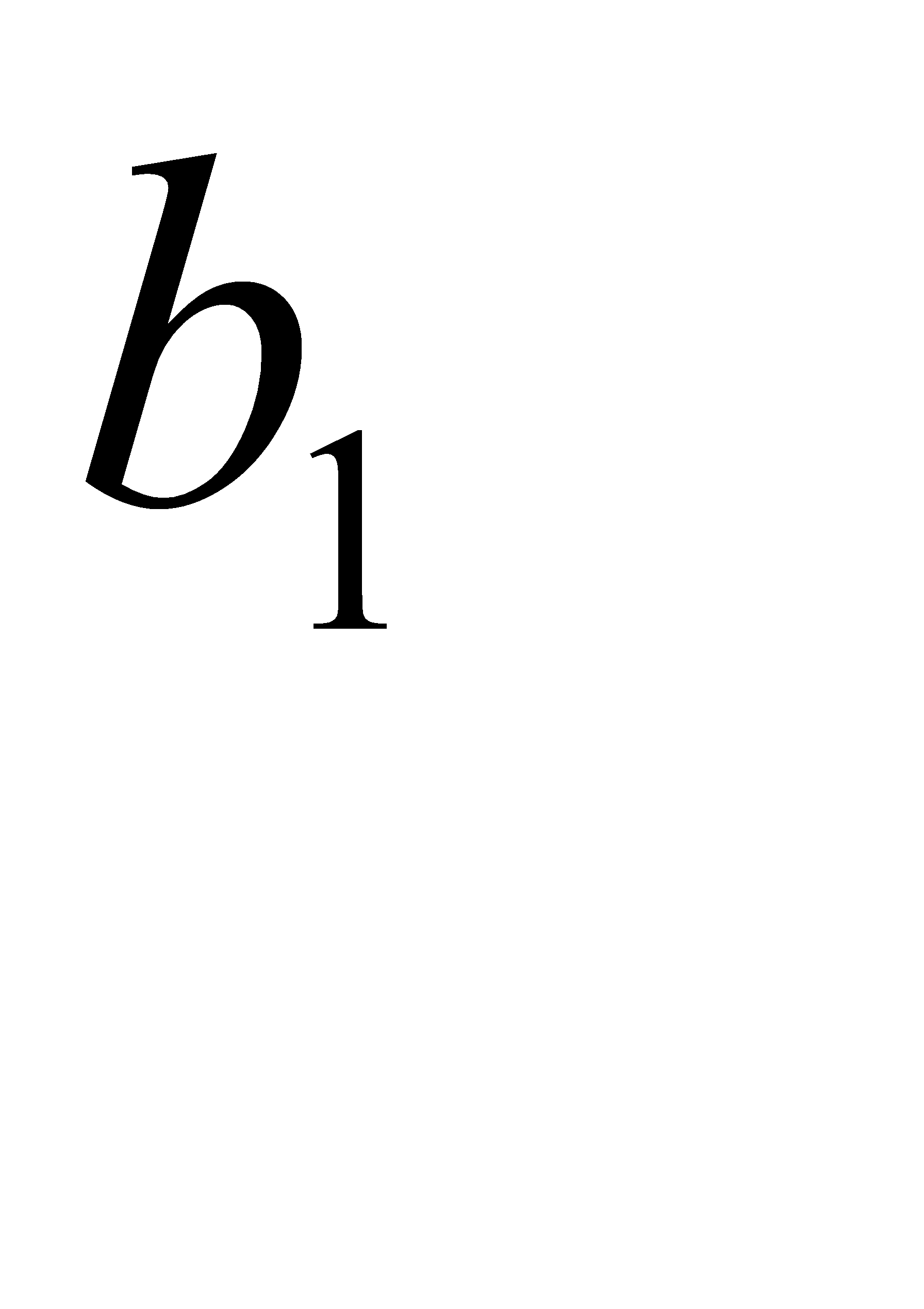
| 0,3 | 0,3 | 0,3 | 0,3 | 0,3 | 0,4 | 0,6 | 0 | 1 | 00 | 00 | 00 | 00 | 00 |
|
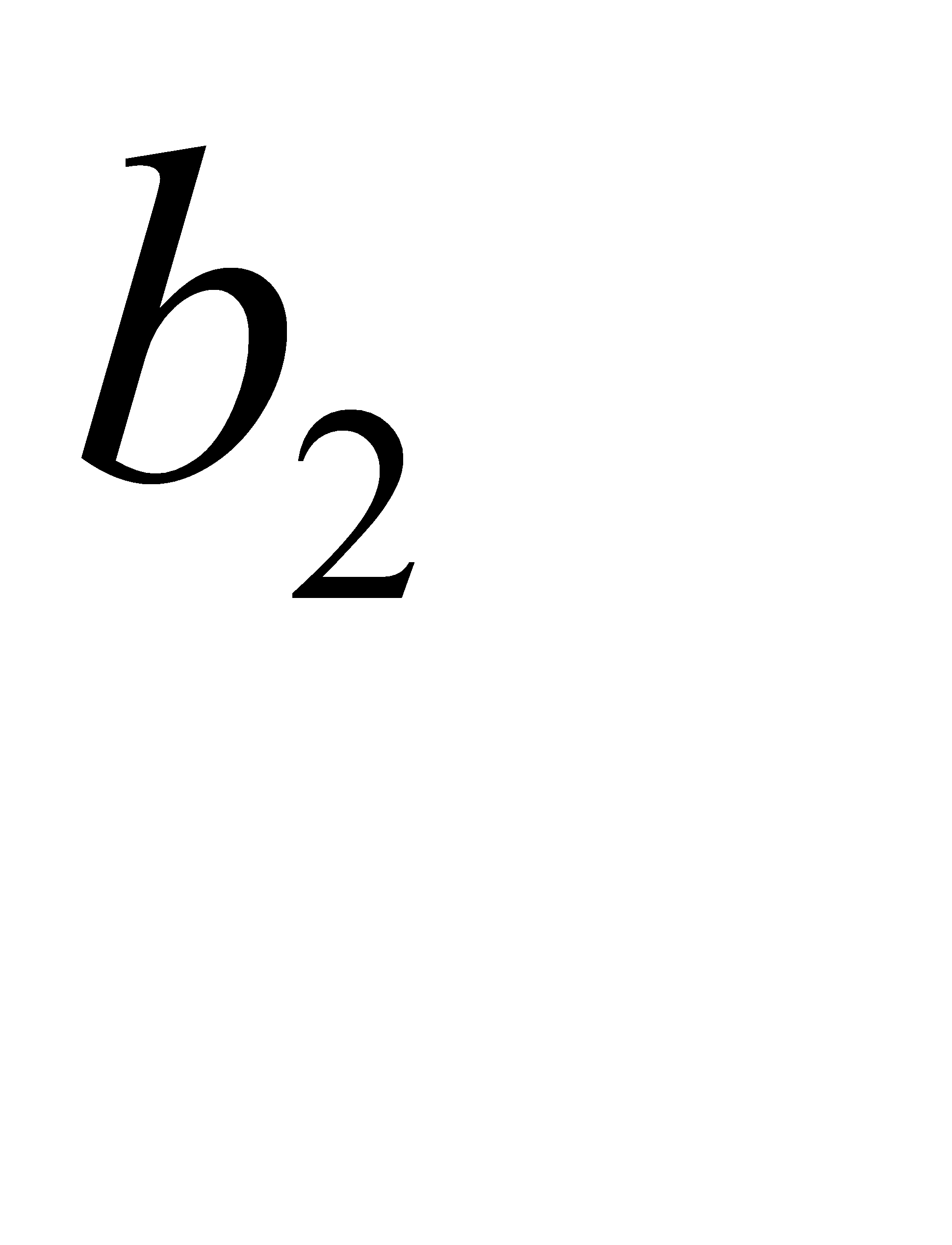
| 0,2 | 0,2 | 0,2 | 0,2 | 0,3 | 0,3 | 0,4 | 1 | 00 | 01 | 10 | 10 | 10 | 10 |
|
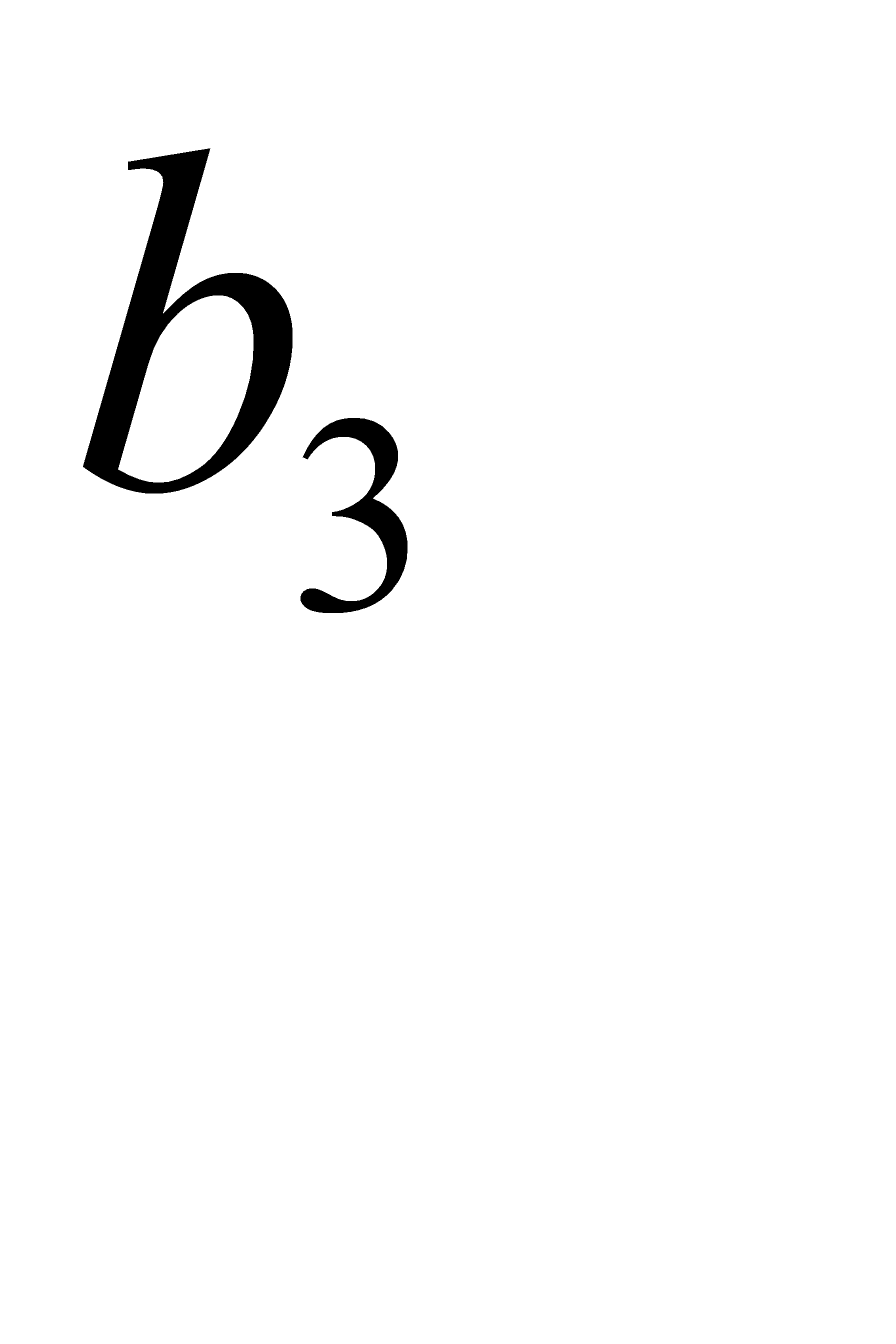
| 0,15 | 0,15 | 0,15 | 0,2 | 0,2 | 0,3 | 01 | 10 | 11 | 010 | 010 | 010 | ||
|
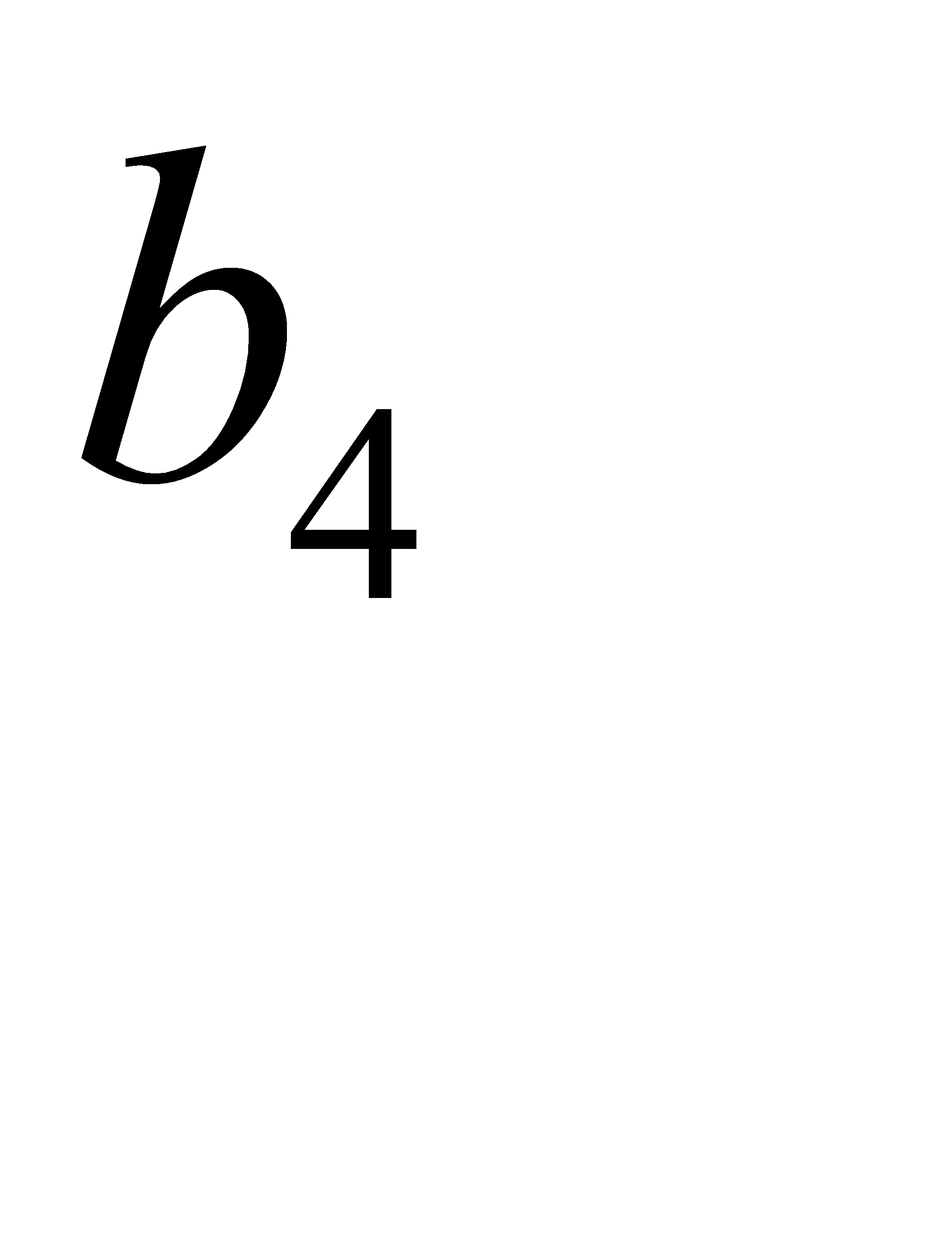
| 0,1 | 0,1 | 0,15 | 0,15 | 0,2 | 11 | 010 | 011 | 110 | 110 | ||||
|
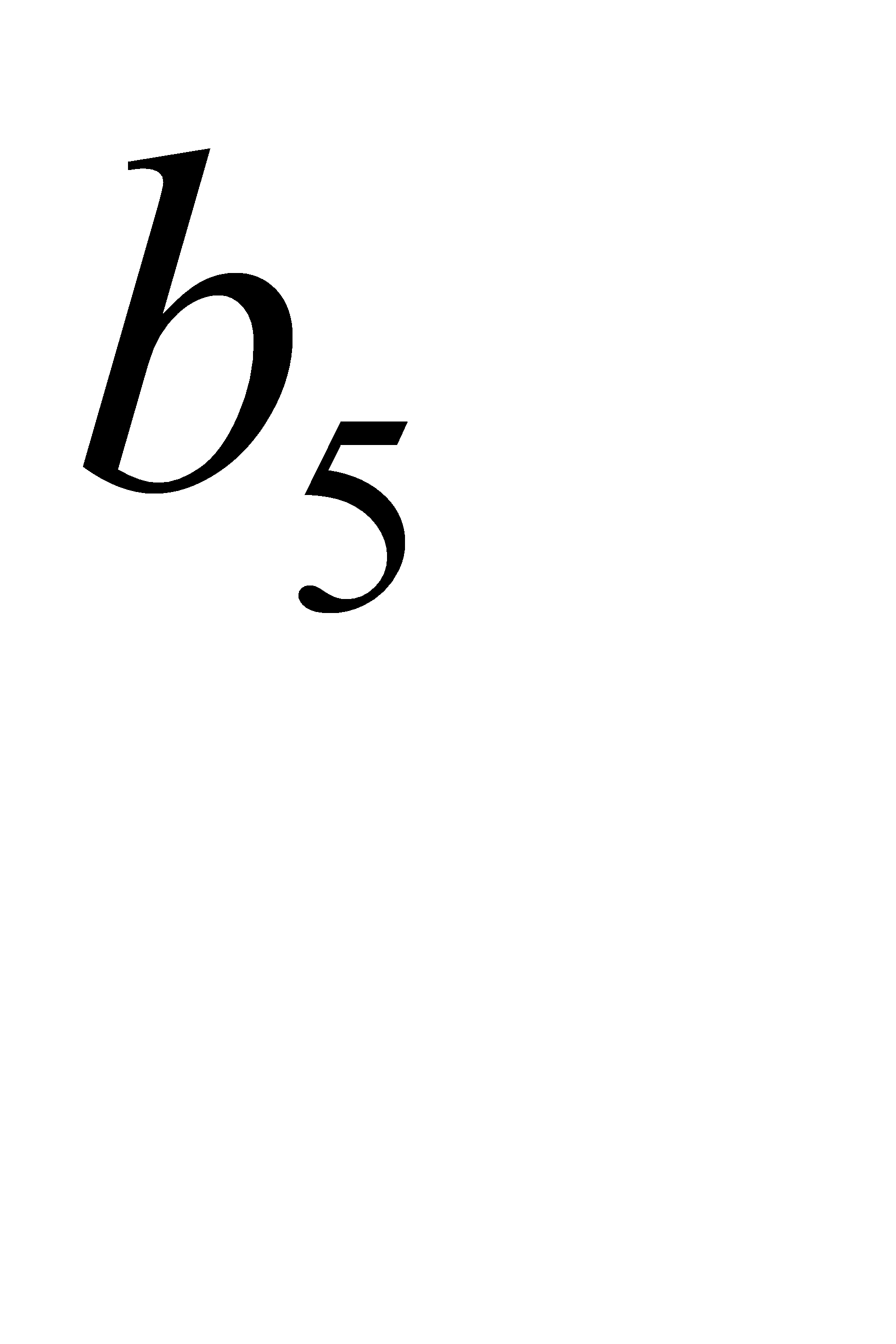
| 0,1 | 0,1 | 0,1 | 0,15 | 011 | 110 | 111 | 111 | ||||||
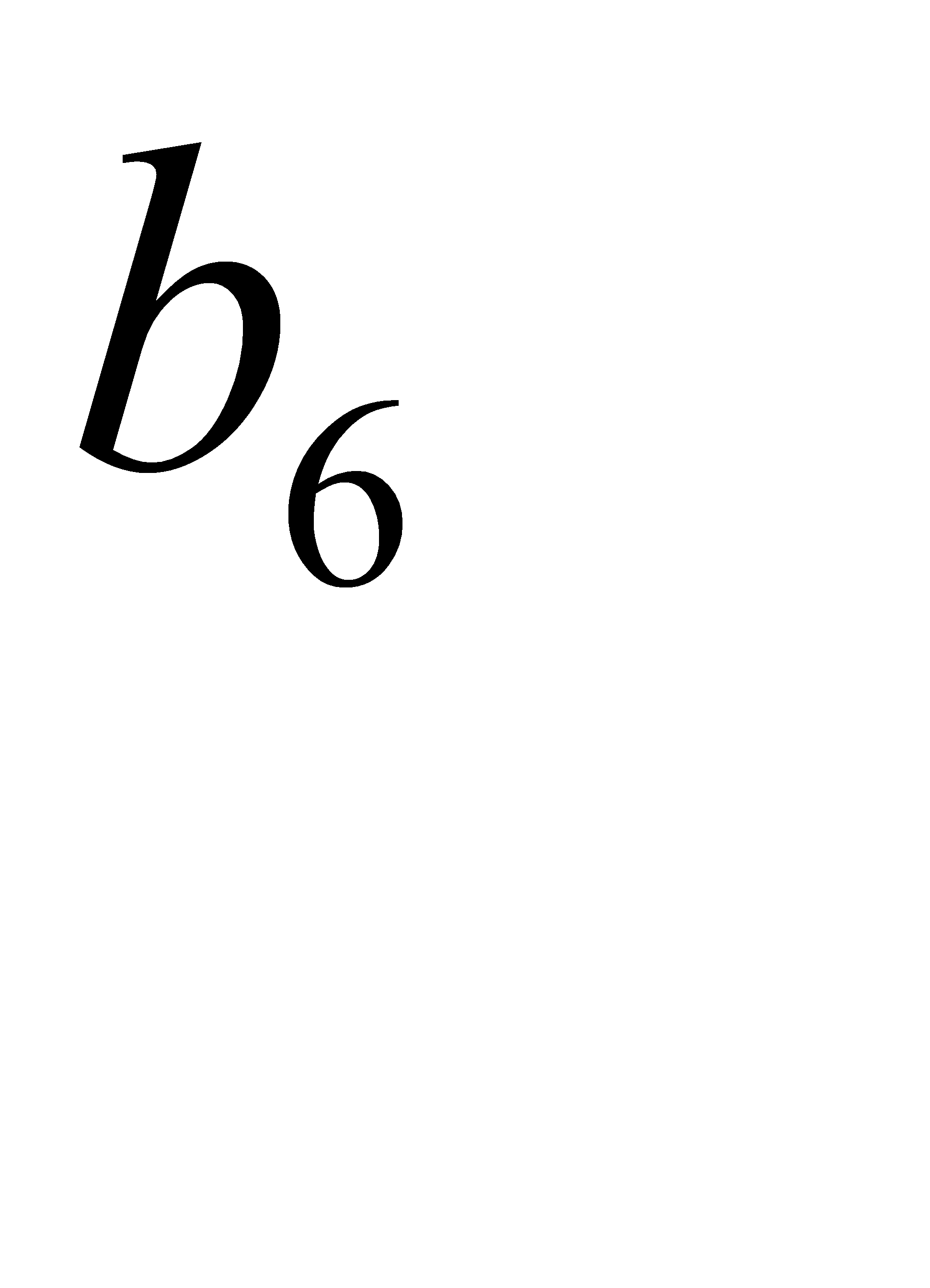
| 0,06 | 0,09 | 0,1 | 111 | 0110 | 0111 | ||||||||
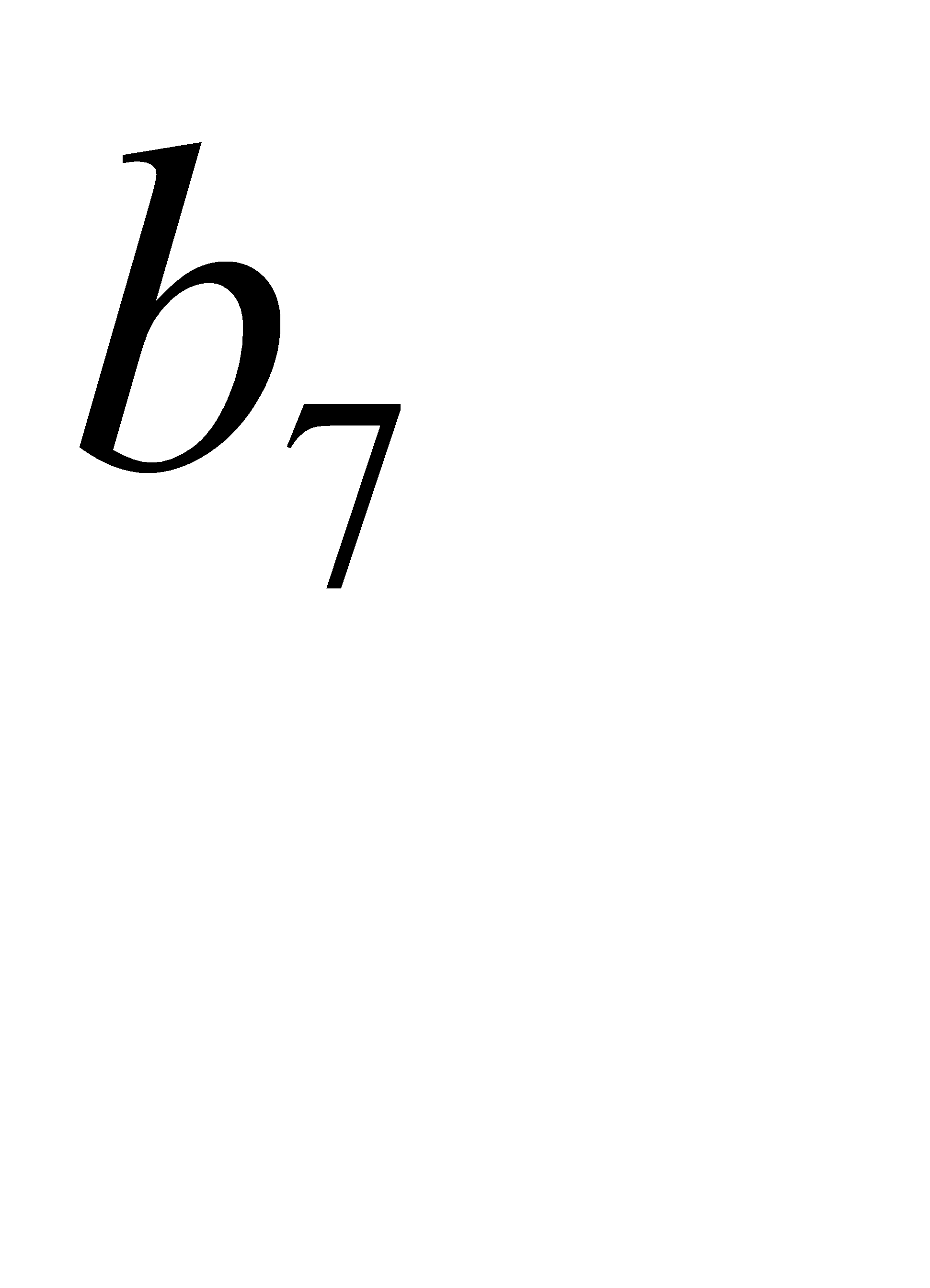
| 0,05 | 0,06 | 0111 | 01100 | ||||||||||
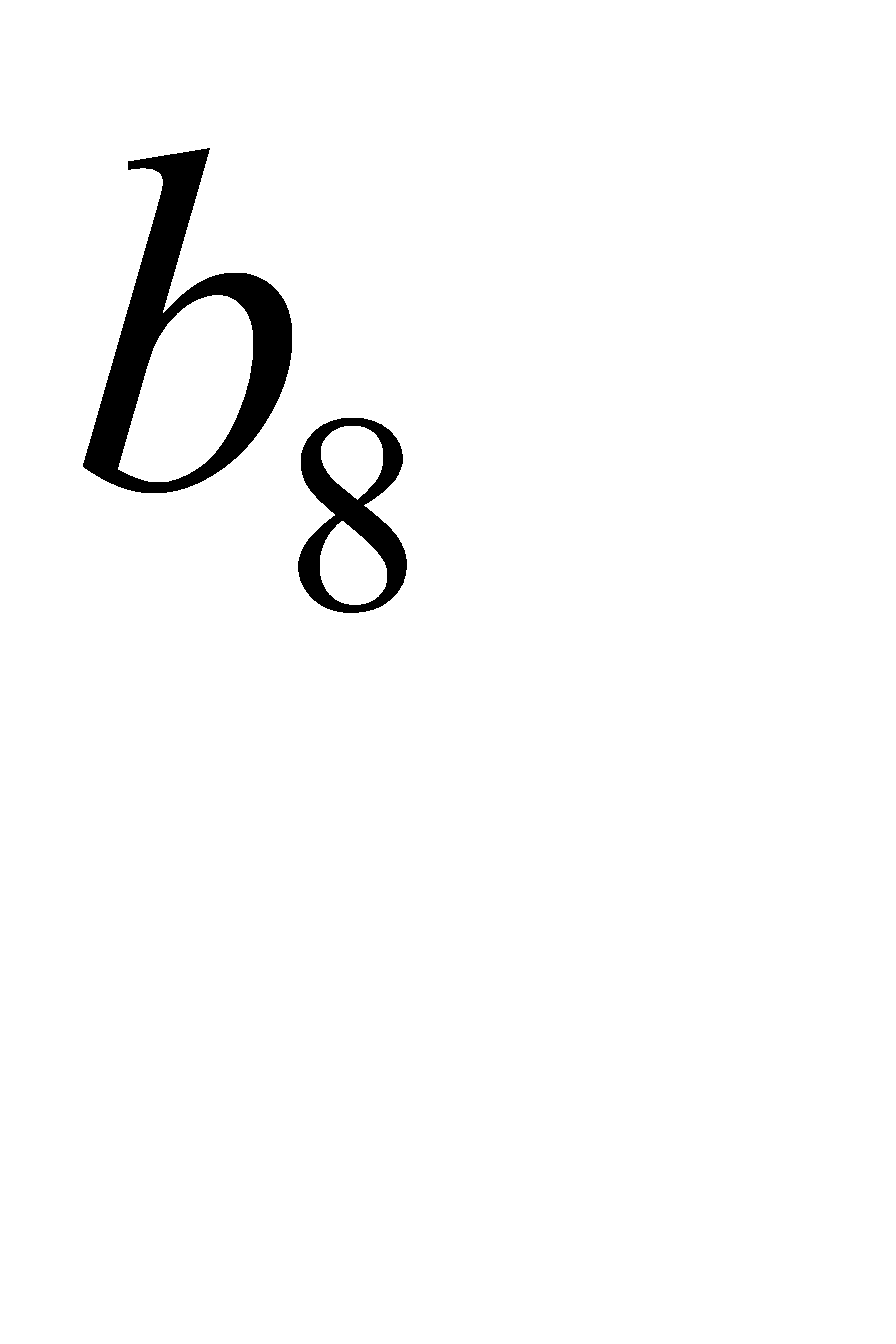
| 0,04 | 01101 |
Ниже на рисунке представлено кодовое дерево.
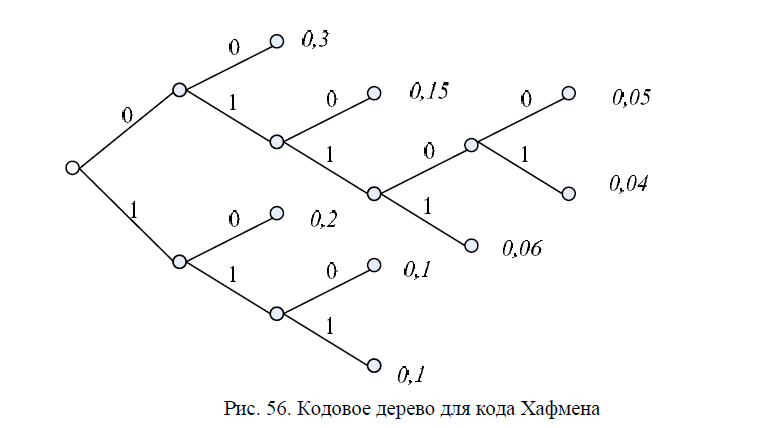
Пример. Источник генерирует знак х1 c вероятностью 0,8 и знак х2 с вероятностью 0,2. Построить эффективные коды Шеннона-Фано и Хаффмана для произвольной последовательности из трех знаков. Определить среднее число символов на знак. Сравнить с энтропией источника.
Энтропия источника:
H= - (0,8·log20,8+0,2·log20,2)=0,722.
Для наиболее наглядного сравнения энтропии источника со средним значением длины кодового обозначения рассмотрим всевозможные комбинации знаков.
Применим метод Шеннона-Фано.
Среднее количество символов в коде (длина): 1·0,8+1·0,2=1. Среднее число символов на знак равно 1, что на 28% больше энтропии.
Построим код Шеннона-Фано для всех возможных двух-знаковых комбинаций.
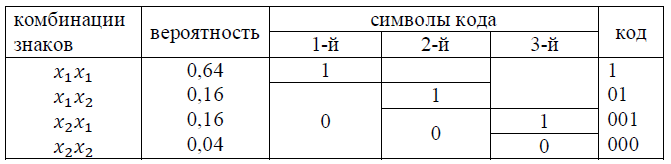
Среднее количество символов в коде (длина): 1·0,64+2·0,16+3·(0,16+0,04)=1,56. Среднее число символов на знак равно 1,56/2=0,78, что на 6% больше энтропии.
Построим код Шеннона-Фано для возможных трех-знаковых комбинаций.
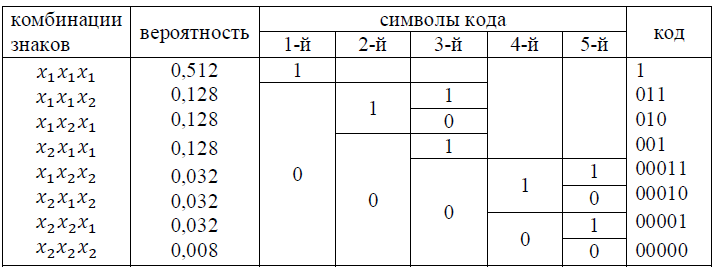
Среднее количество символов в коде - 2,184. Среднее число символов на знак равно 0,728, что на 0,8% больше энтропии. Самостоятельно построить Хаффмена и убедиться в том, что коды Шеннона-Фано и Хаффмена совпали.
Вопросы практической реализации алгоритма. Для повышения эффективности сжатия необходимо, чтобы при построении кодового дерева использовались данные по вероятностям появления букв именно в этом файле, а не усредненные по большому количеству текстов. Исходя из этого, необходима статистика встречаемости букв сжимаемого файла, которая может быть получена предварительным проходом по файлу.
Для ускорения работы принято определять не вероятности появления букв, а частоту встречаемости (количество появлений) буквы в файле. Это позволяет существенно упростить и ускорить алгоритм (не нужно медленных операций с плавающей запятой и операций деления). При таком подходе алгоритм работы не изменяется, так как частоты прямо пропорциональны вероятностям. Стоит заметить, что вес корневого узла дерева кодирования в таком случае будет равен общему количеству букв в обрабатываемом файле.
Применение кодирования Хаффмена. С тех пор, как Д.А. Хаффмен опубликовал свою работу «Метод построения кодов с минимальной избыточностью», его алгоритм кодирования стал базой для огромного количества дальнейших исследований в этой области. Сжатие данных по Хаффмену применяется при сжатии фото- и видеоизображений (JPEG, стандарты сжатия MPEG), в архиваторах (PKZIP, LZH и др.), в протоколах передачи данных MNP5 и MNP7.
По сей день в компьютерных журналах можно найти большое количество публикаций, посвященных как различным реализациям алгоритма Хаффмена, так и поискам его лучшего применения. Кодирование Хаффмена используется в коммерческих программах сжатия, встроено в некоторые телефаксы и даже используется в алгоритме JPEG сжатия графических изображений с потерями. Применение кода Хаффмена гарантирует возможность декодирования.
Недостатки метода Хаффмана:
· для восстановления содержимого сжатого текста при декодировании необходимо знать таблицу частот, которую использовали при кодировании. Следовательно, длина сжатого текста увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию данных.
· необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по тексту: одного для построения модели текста (таблицы частот и дерева Хаффмена), другого для собственно кодирования.
· требуется два просмотра сжимаемого файла: первый для построения требуемой таблицы, а второй уже для сжатия.
· минимальная длина кодового слова не может быть меньше единицы, тогда как энтропия сообщения вполне может составлять и 0,1, и 0,01 бит/букву. В этом случае код Хаффмана становится существенно избыточным. Проблема решается применением алгоритма к блокам символов, но тогда усложняется процедура кодирования/декодирования;
· код Хаффмена обеспечивает среднюю длину кода, совпадающую с энтропией, только в том случае, когда вероятности символов источника являются целыми отрицательными степенями двойки: 1/2 = 0,5; 1/4 = 0,25; 1/8 = 0,125 и т.д. На практике же такая ситуация встречается очень редко
Избавиться от этих недостатков позволяет алгоритм адаптивного кодирования все по тому же Хаффмену.
В заключение хотелось бы отметить, что со времени опубликования, код Хаффмена все же ничуть не потерял своей актуальности и значимости. Так с уверенностью можно сказать, что мы сталкиваемся с ним, в той или иной форме практически каждый раз, когда архивируем файлы, смотрим фотографии, фильмы, посылаем факс или слушаем музыку. Преимуществами данных методов является их очевидная простота реализации и, как следствие этого, высокая скорость кодирования и декодирования.
Биография Д. Хаффмена. Дэвид Хаффмен родился в 1925 году в штате Огайо (Ohio), США. Хаффмен получил степень бакалавра электротехники в государственном университете Огайо (Ohio State University) в возрасте 18 лет. Затем он служил в армии офицером поддержки радара на эсминце, который помогал обезвреживать мины в японских и китайских водах после Второй Мировой Войны. Впоследствии он получил степень магистра в университете Огайо и степень доктора в Массачусетском Институте Технологий (Massachusetts Institute of Technology - MIT). Хотя Хаффмен больше известен за разработку метода построения минимально-избыточных кодов, он так же сделал важный вклад во множество других областей (по большей части в электронике). Он долгое время возглавлял кафедру Компьютерных Наук в MIT. В 1974, будучи уже заслуженным профессором, он подал в отставку. Хаффмен получил ряд ценных наград. В 1999 - Медаль Ричарда Хамминга (Richard W. Hamming Medal) от Института Инженеров Электричества и Электроники (Institute of Electrical and Electronics Engineers - IEEE) за исключительный вклад в Теорию Информации, Медаль Louis E. Levy от Франклинского Института (Franklin Institute) за его докторскую диссертацию о последовательно переключающихся схемах, Награду W. Wallace McDowell, Награду от Компьютерного Сообщества IEEE, Золотую юбилейную награду за технологические новшества от IEEE в 1998. В октябре 1999 года, в возрасте 74 лет Дэвид Хаффмен скончался от рака.
Код Шеннона – Фано (1961)
Алгоритм метода Шеннона-Фано - один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано, и он имеет большое сходство с алгоритмом Хаффмана.
Алгоритм основан на частоте повторения. Часто встречающийся символ кодируется кодом меньшей длины, а редко встречающийся - кодом большей длины. В свою очередь, коды, полученные при кодировании, префиксные. Это и позволяет однозначно декодировать любую последовательность кодовых слов.
Алгоритм Шеннона-Фано
1. Упорядочиваем по невозрастанию вероятностей (частот) список символов алфавита.
2. Полученная совокупность вероятностей (частот) делится на две последовательные части так, чтобы сумма вероятностей (частот) входящих в них символов как можно меньше отличалась друг от друга.
3. Символам, соответствующим левой части, присваивается код 0, правой - 1. Таким образом, мы получаем листья дерева.
4. Шаг 2-3 повторяется для каждой из полученных частей, если она содержит хотя бы два символа
Таким образом, видно, что алгоритм Хаффмана как бы движется от листьев к корню, а алгоритм Шеннона-Фано, используя деление, движется от корня к листьям. Это отличие позволяет в алгоритме Хаффмана полнее использовать специфику данного распределения вероятностей и строить оптимальный код.
Алгоритм Шеннона-Фано строит код, близкий к оптимальному. При построении кода Шеннона-Фано разбиение множества элементов может быть произведено несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n+1) и привести к не оптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона - Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона-Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона-Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, т.е. оптимальные коды.
Пример. Провести эффективное кодирование ансамбля из восьми знаков:
| Буква (знак) | Вероятность | Кодовые | р i q i | -р i log р i | |||||||||||
| x i | Рi | последовательности | Длина | ||||||||||||
| q i | |||||||||||||||
| Номер разбиения | |||||||||||||||
|
|
|
|
| ||||||||||||
|
| 1 | 2 | 3 | 4 | |||||||||||
|
|
|
|
| ||||||||||||
| x1 | 0,25 | 1 | 1 |
| 2 | 0,5 | 0,50 | ||||||||
|
|
|
|
| ||||||||||||
| x2 | 0,25 | 1 | 0 |
| 2 | 0,5 | 0,50 | ||||||||
|
|
|
|
| ||||||||||||
| x3 | 0,15 | 0 | 1 | 1 | 3 | 0,45 | 0,41 | ||||||||
|
|
|
|
| ||||||||||||
| x4 | 0,15 | 0 | 1 | 0 |
| 3 | 0,45 | 0,41 | |||||||
|
|
|
| |||||||||||||
| x5 | 0,05 | 0 | 0 | 1 | 1 | 4 | 0,2 | 0,22 | |||||||
|
|
|
| |||||||||||||
| x6 | 0,05 | 0 | 0 | 1 | 0 | 4 | 0,2 | 0,22 | |||||||
|
|
|
| |||||||||||||
| x7 | 0,05 | 0 | 0 | 0 | 1 | 4 | 0,2 | 0,22 | |||||||
|
|
|
| |||||||||||||
| x8 | 0,05 | 0 | 0 | 0 | 0 | 4 | 0,2 | 0,22 | |||||||
|
|
|
| |||||||||||||
Среднее количество символов в коде равно энтропии источника. Данный код является оптимальным.
Пример. Построить таблицу кодов алфавита методом Шенно-Фано. Записать двоичным кодом фразу «теория информации».
Составим таблицу кодов алфавита указанным методом.
Таблица. Коды русского алфавита по методу Шенно-Фано
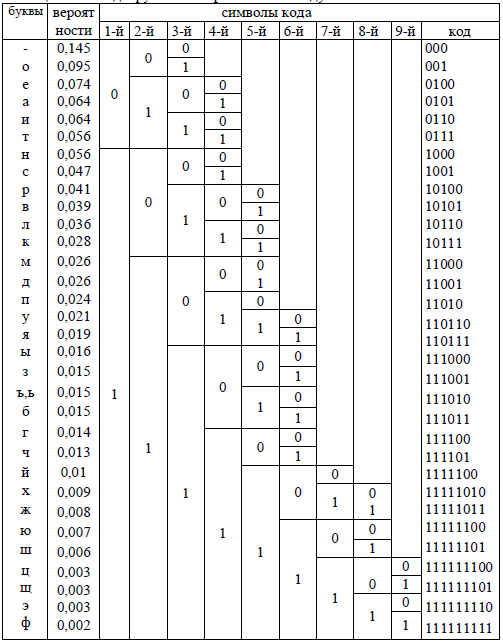
Фраза «теория информации» будет выглядеть следующим образом:
Пример. Построить код, используя алгоритм Шеннона-Фано для алфавита 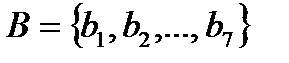с заданным распределением вероятностей 
.
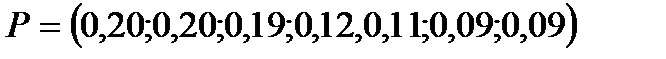На каждом шаге алгоритма упорядоченную по невозрастанию последовательность вероятностей (частот) символов алфавита делим на две части так, чтобы сумма вероятностей (частот) входящих символов как можно меньше отличалась друг от друга.
Данную процедуру можно оформить иначе, в виде таблицы:
| Символ | Вероятность | Деление на группы | Код | ||||
|
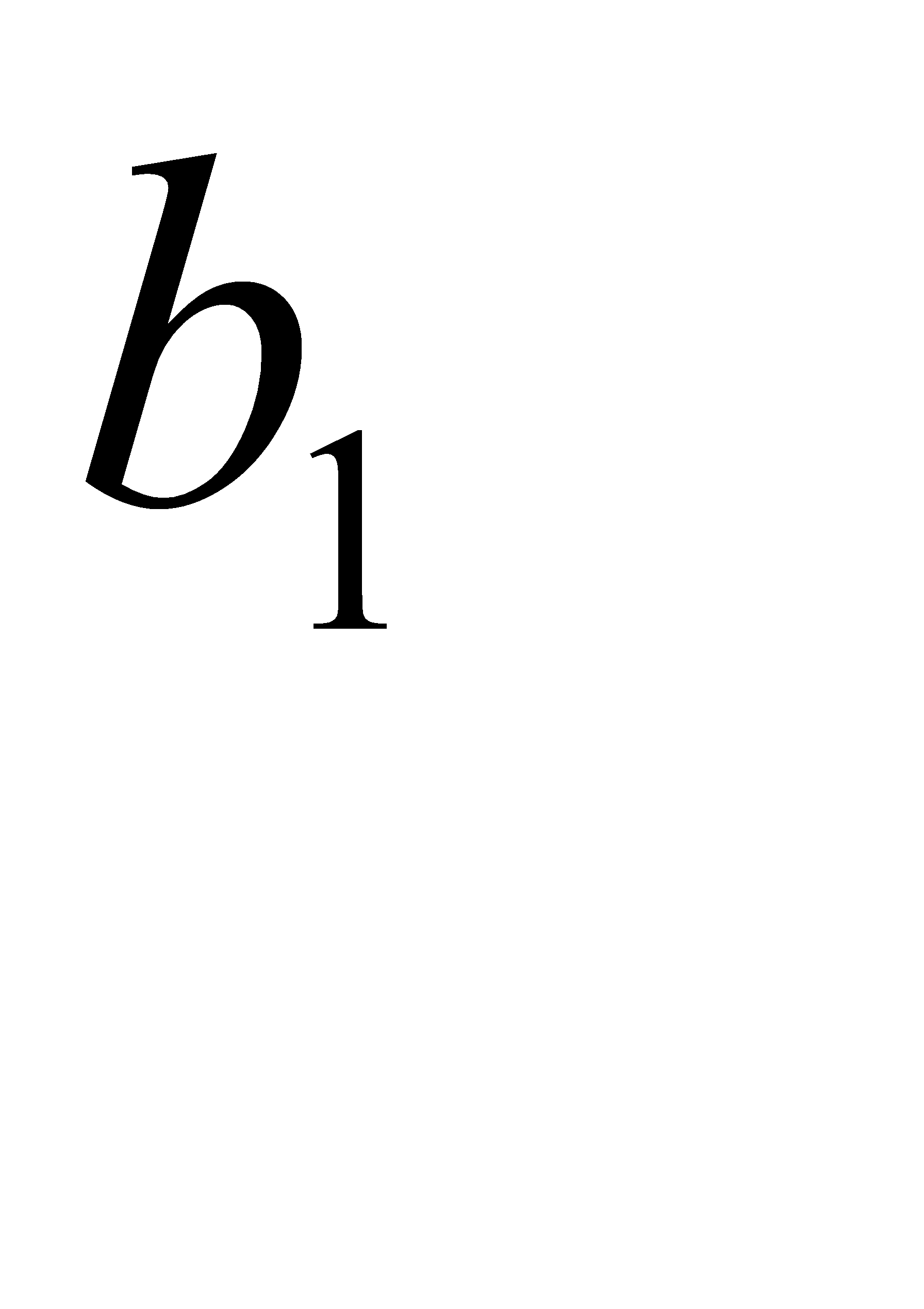
| 0,2 |
| 
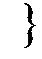
| 0 | 0 | ||
|
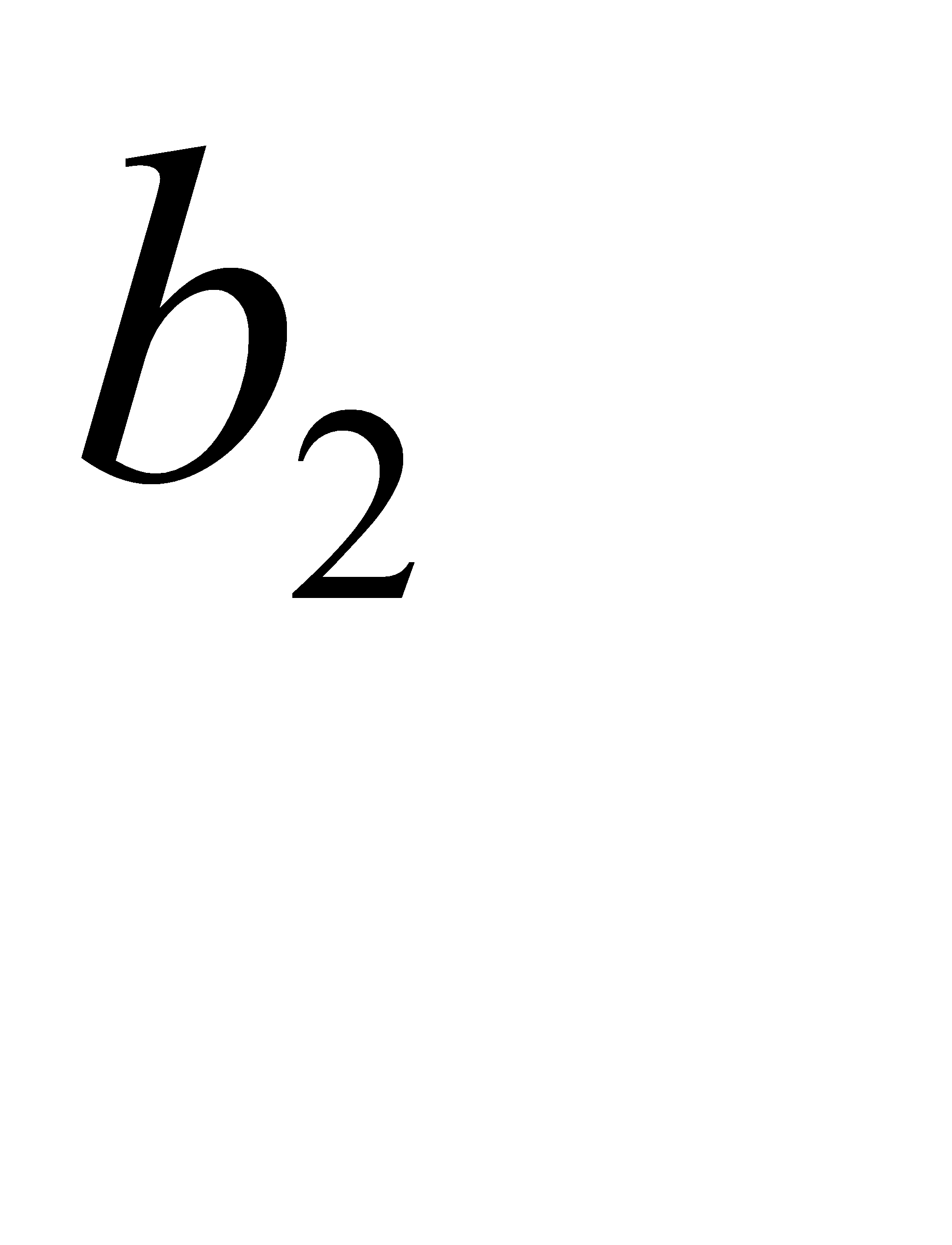
| 0,2 |
|
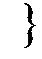
| 0 | 1 | 0 | |
|
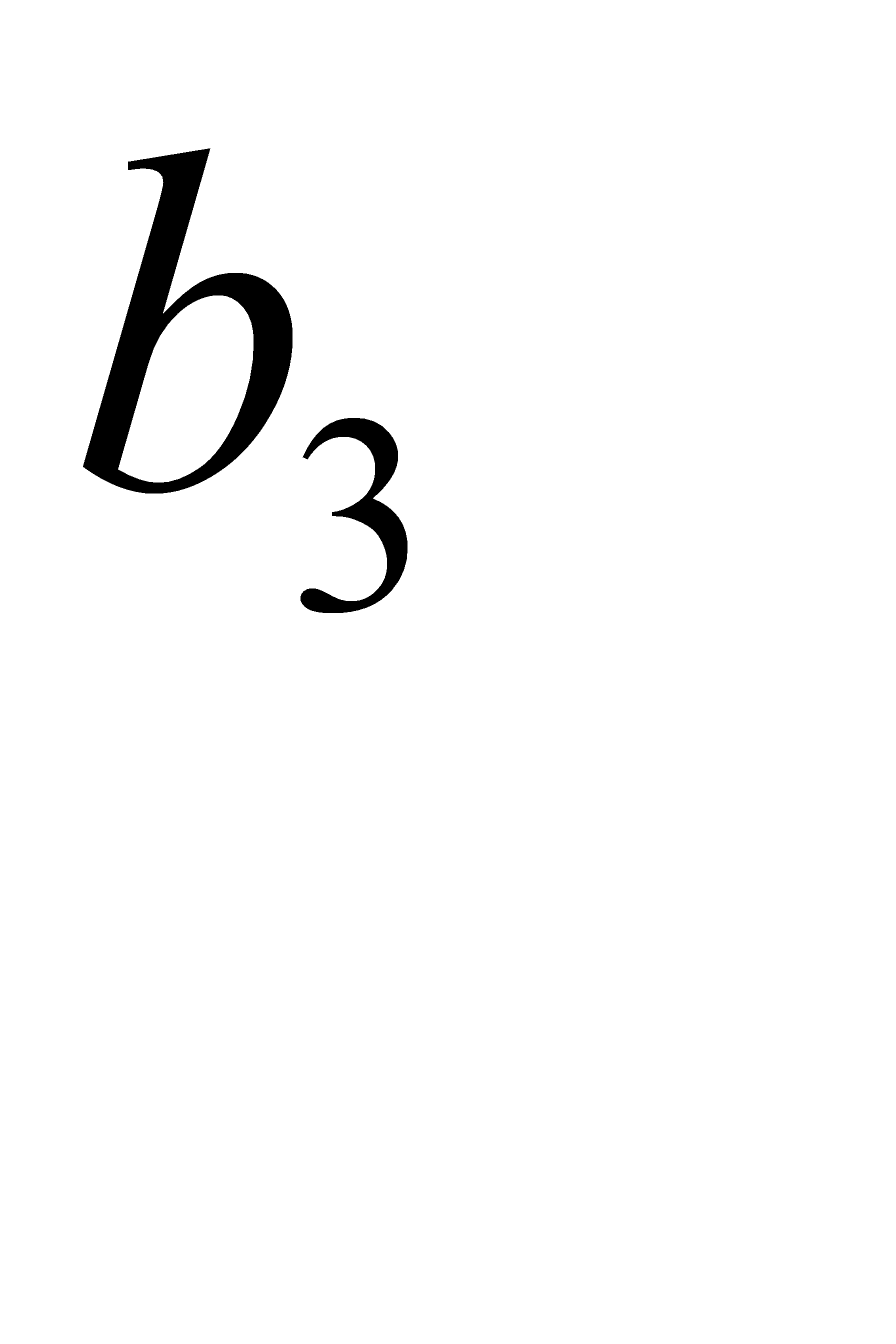
| 0,19 |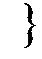
| 0 | 1 | 1 | ||
|
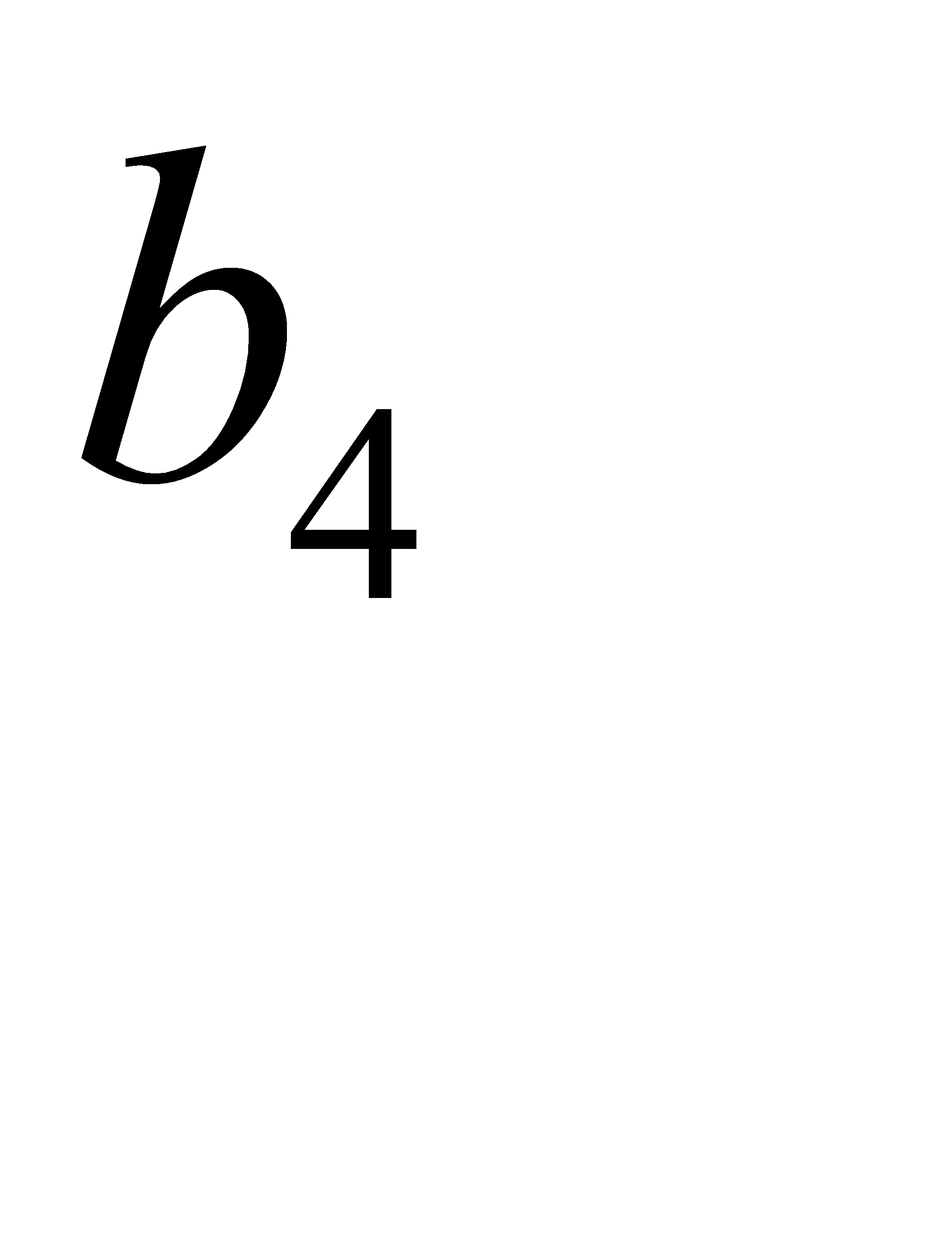
| 0,12 |
|
|
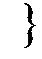
| 1 | 0 | 0 |
|
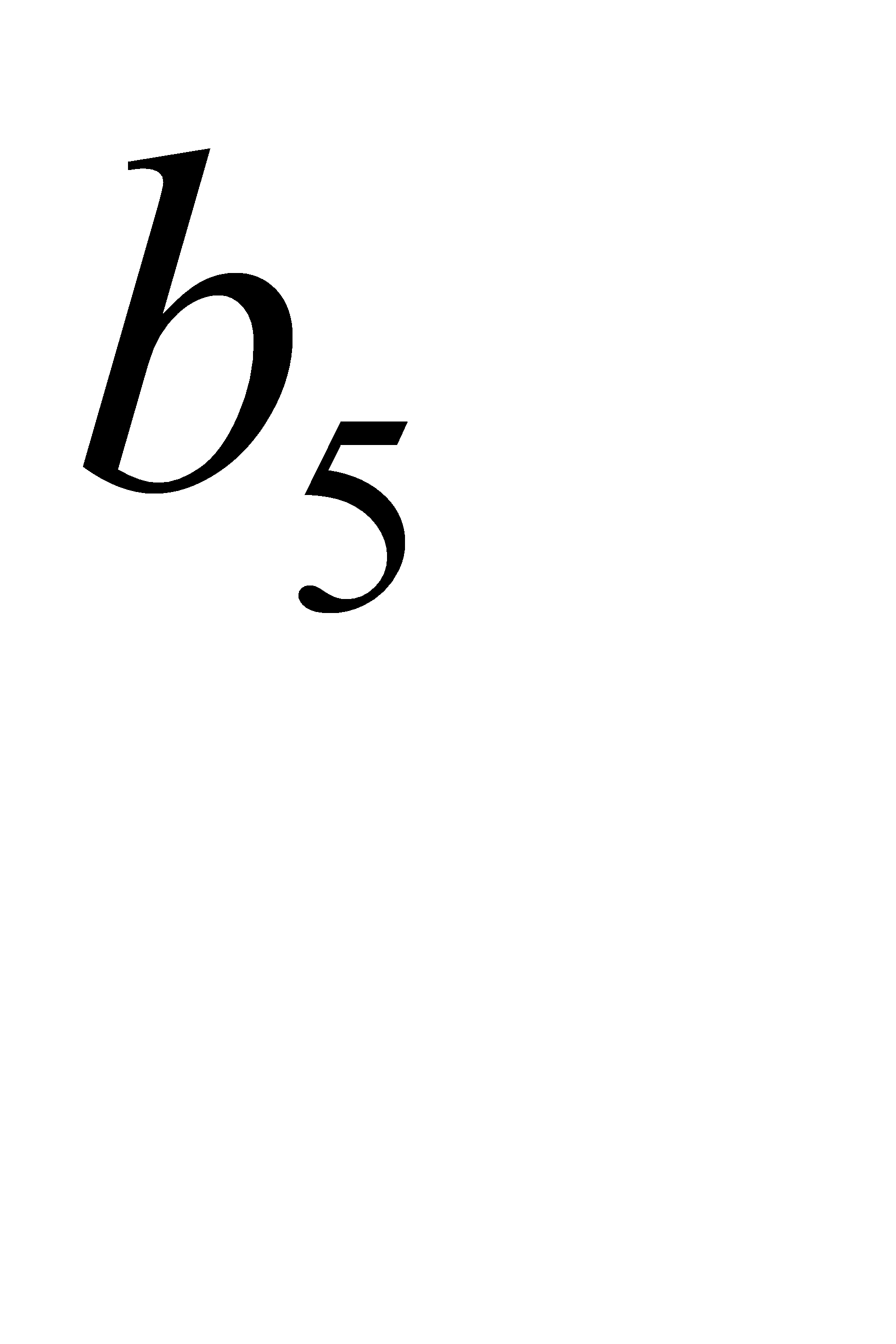
| 0,11 |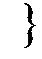
| 1 | 0 | 1 | ||
|
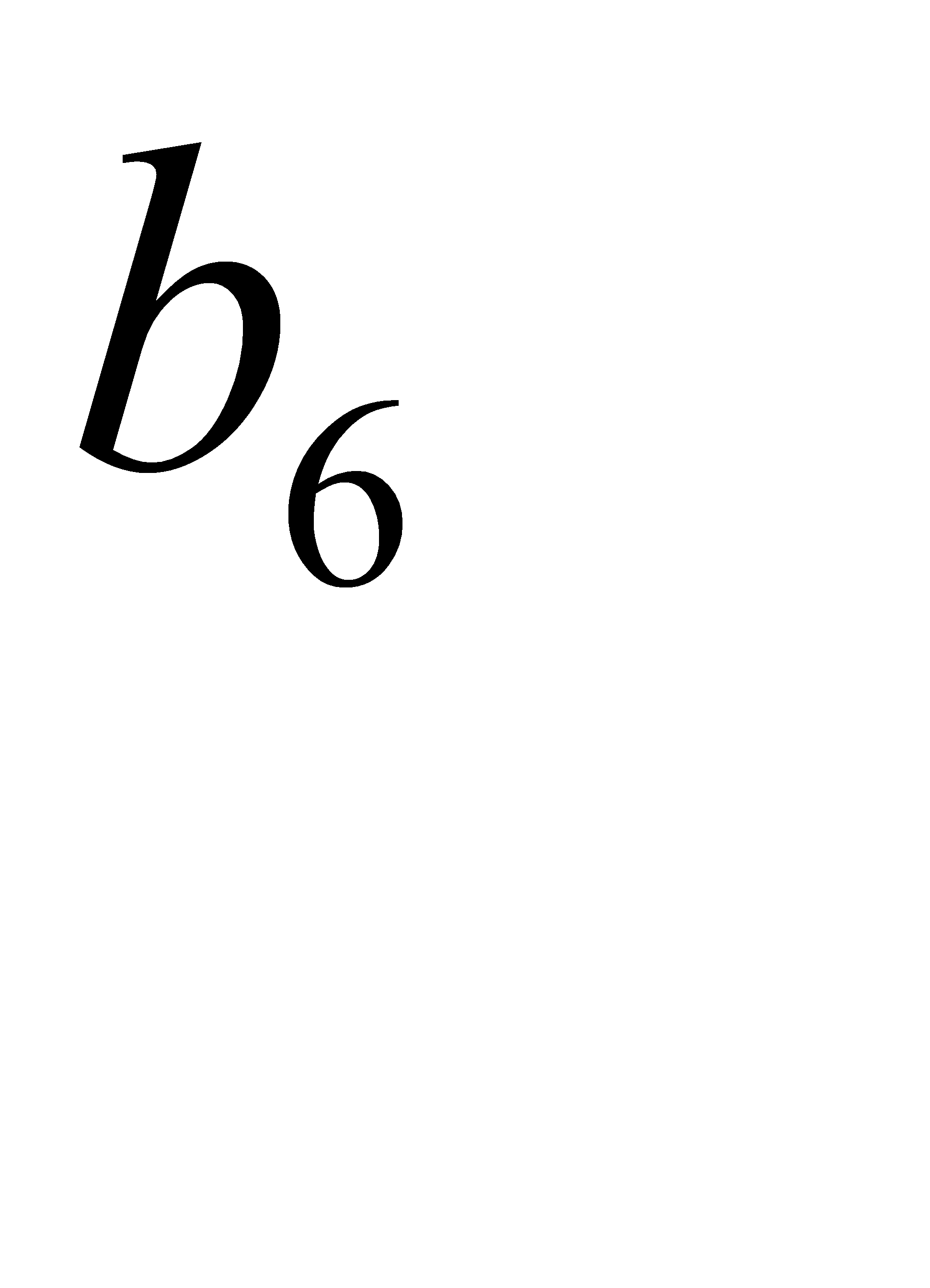
| 0,09 |
|
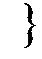
| 1 | 1 | 0 | |
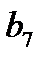
| 0,09 |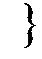
| 1 | 1 | 1 | ||
Получаем следующую схему алфавитного кодирования:
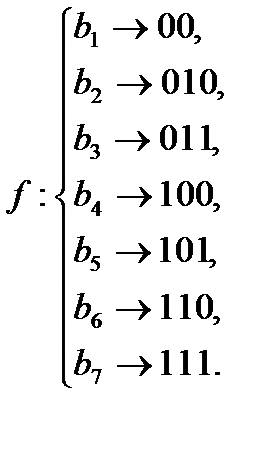
Стоимость кодирования равна
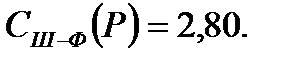
Пример. Построить код, используя алгоритм Шеннона-Фано для алфавита, состоящего из семи символов, с вероятностями, указанными в таблице.
| а | в | л | и | е | с | к |
| 0.3 | 0.2 | 0.15 | 0.1 | 0.1 | 0.08 | 0.07 |
Процедура кодирования представлена в виде таблицы ниже.
| Символ |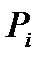 
| Деление на группы | Кодовое слово | ||||||
| а | 0,3 |
|
| 0 | 0 | ||||
| в | 0,2 |
| 0 | 1 | |||||
| л | 0,15 |
|
|
| 1 | 0 | 0 | ||
| и | 0,1 |
| 1 | 0 | 1 | ||||
| е | 0,1 |
|
| 1 | 1 | 0 | |||
| с | 0,08 |
|
| 1 | 1 | 1 | 0 | ||
| к | 0,07 |
| 1 | 1 | 1 | 1 | |||
В соответствии с приведенным алгоритмом получаем таблицу кодов для символов алфавита:
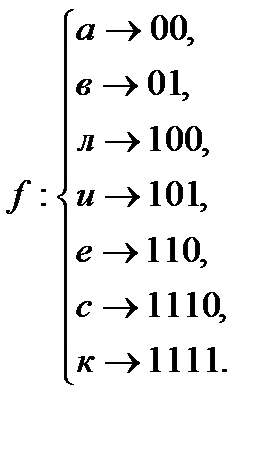
Пусть входное сообщение: «вилка». Выходная последовательность кодов: 01101100111100. Если входная последовательность кодов: 1000101111000. Сообщение на выходе: «лиса».
Пример. Построить код, используя алгоритм Шеннона-Фано для распределения вероятностей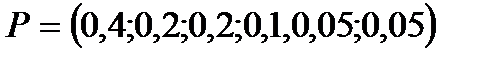 
.
| Символ |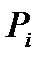
| Деление на группы | Кодовое слово | ||||||||
|
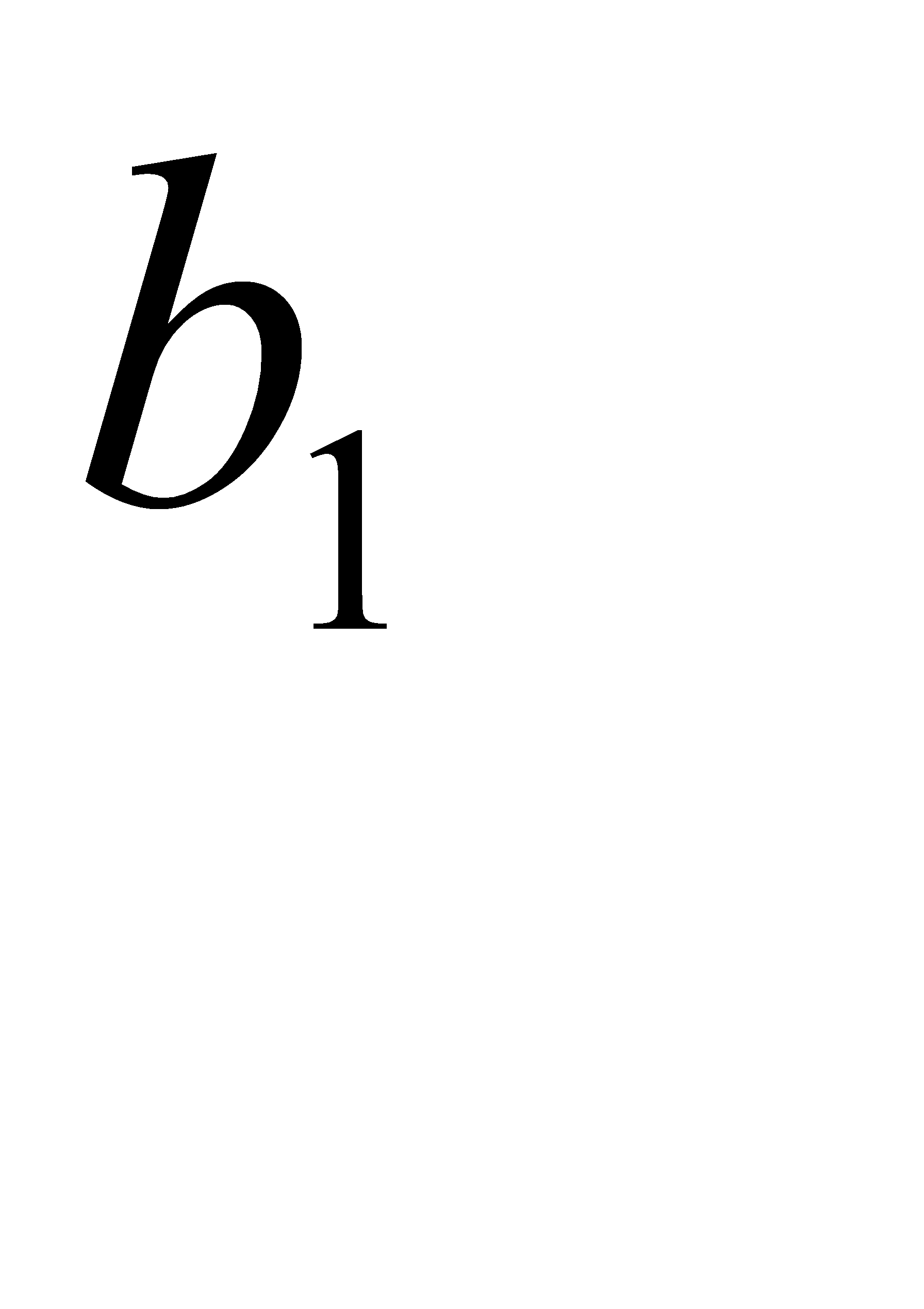
| 0,4 |
| 0 | ||||||||
|
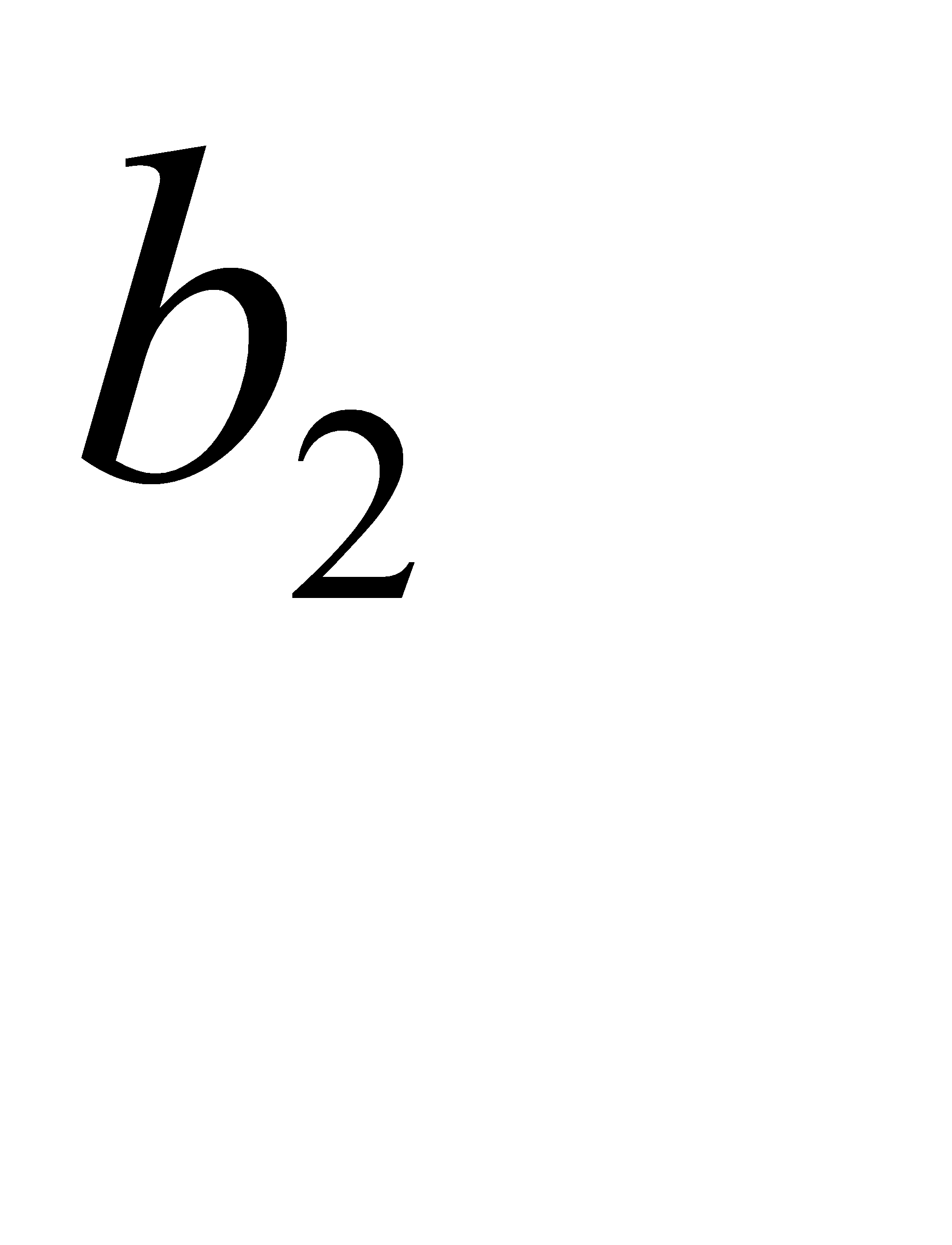
| 0,2 |
|
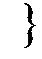
| 1 | 0 | ||||||
|
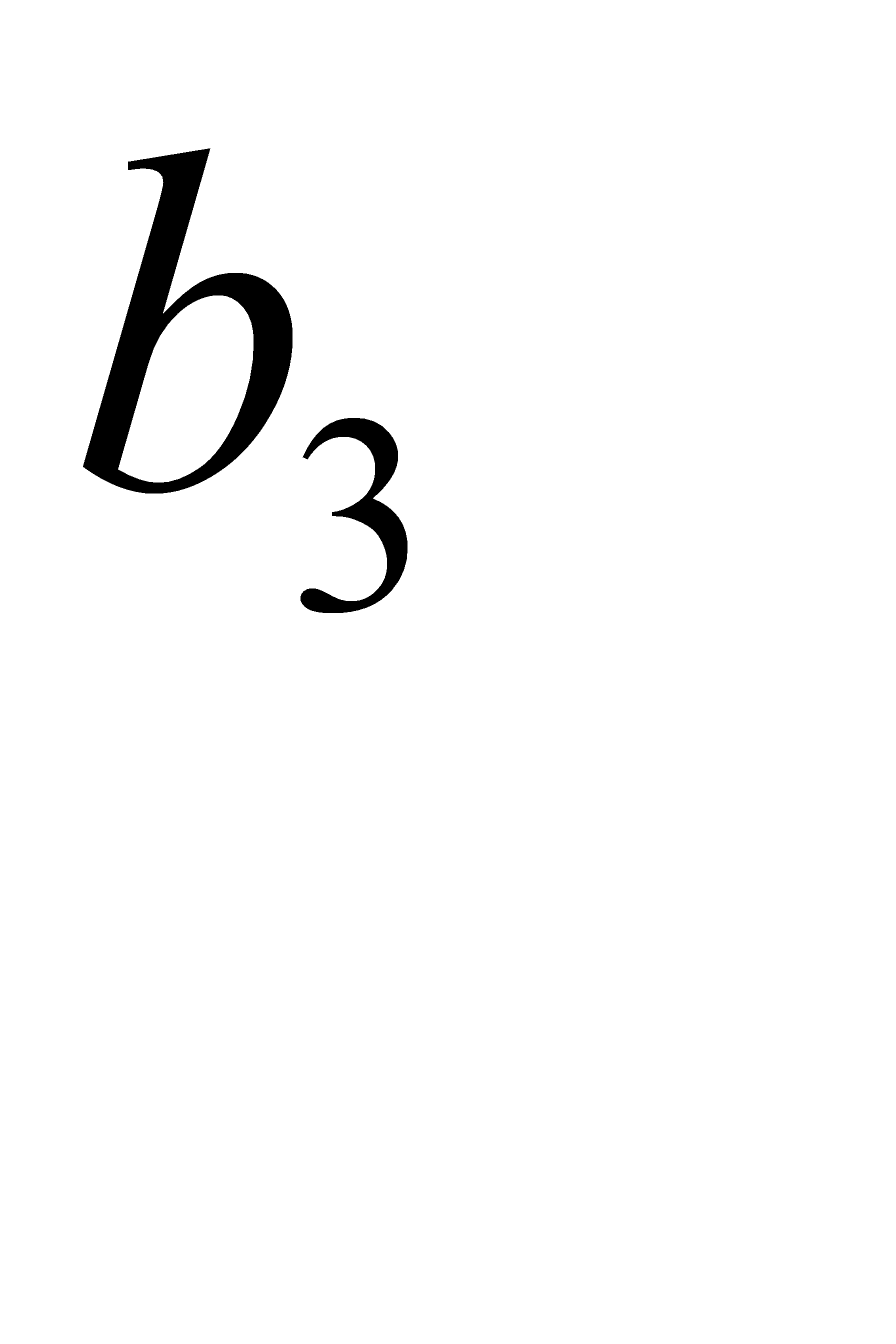
| 0,2 |
| 
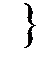
| 1 | 1 | 0 | |||||
|
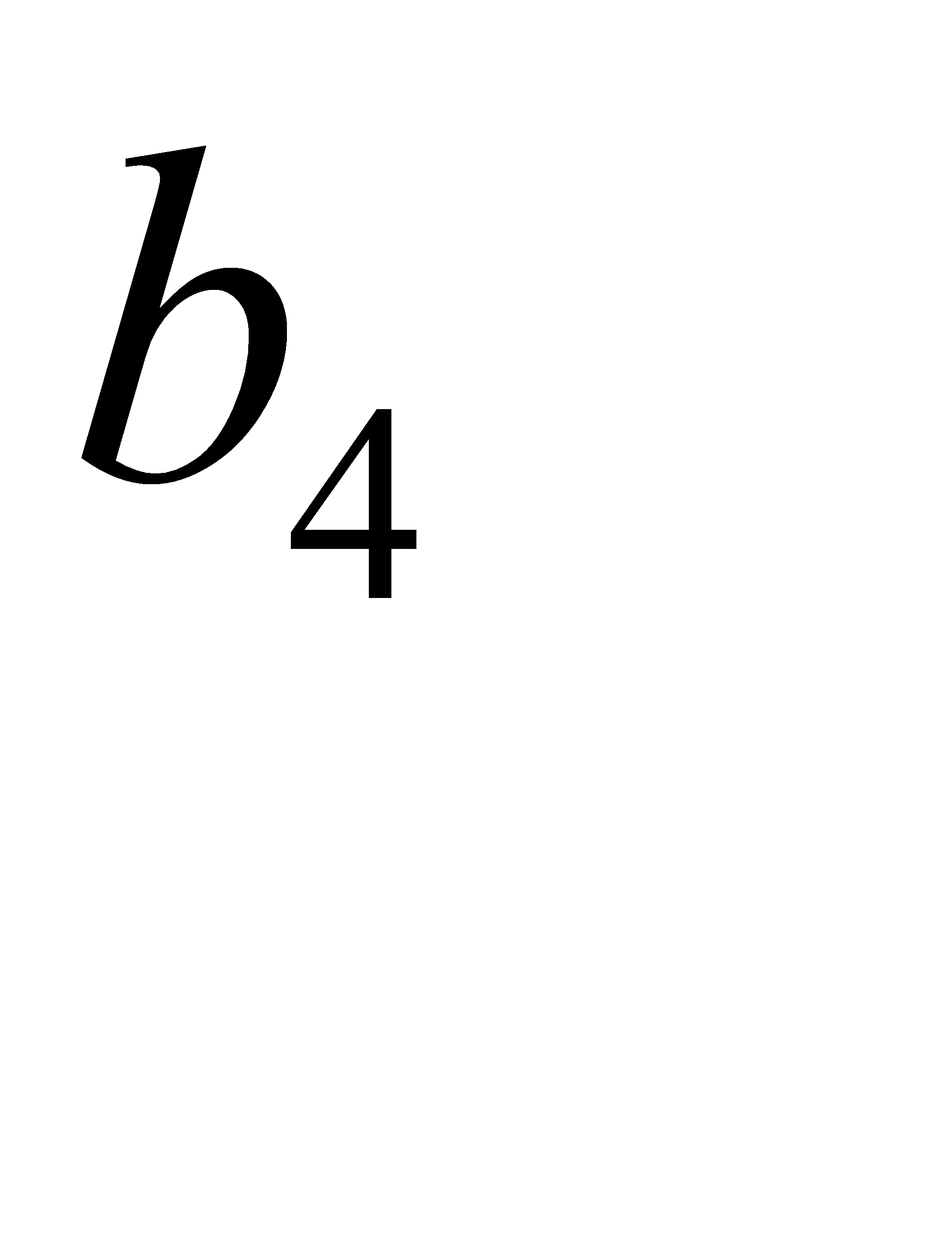
| 0,1 |
|
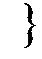
| 1 | 1 | 1 | 0 | ||||
|
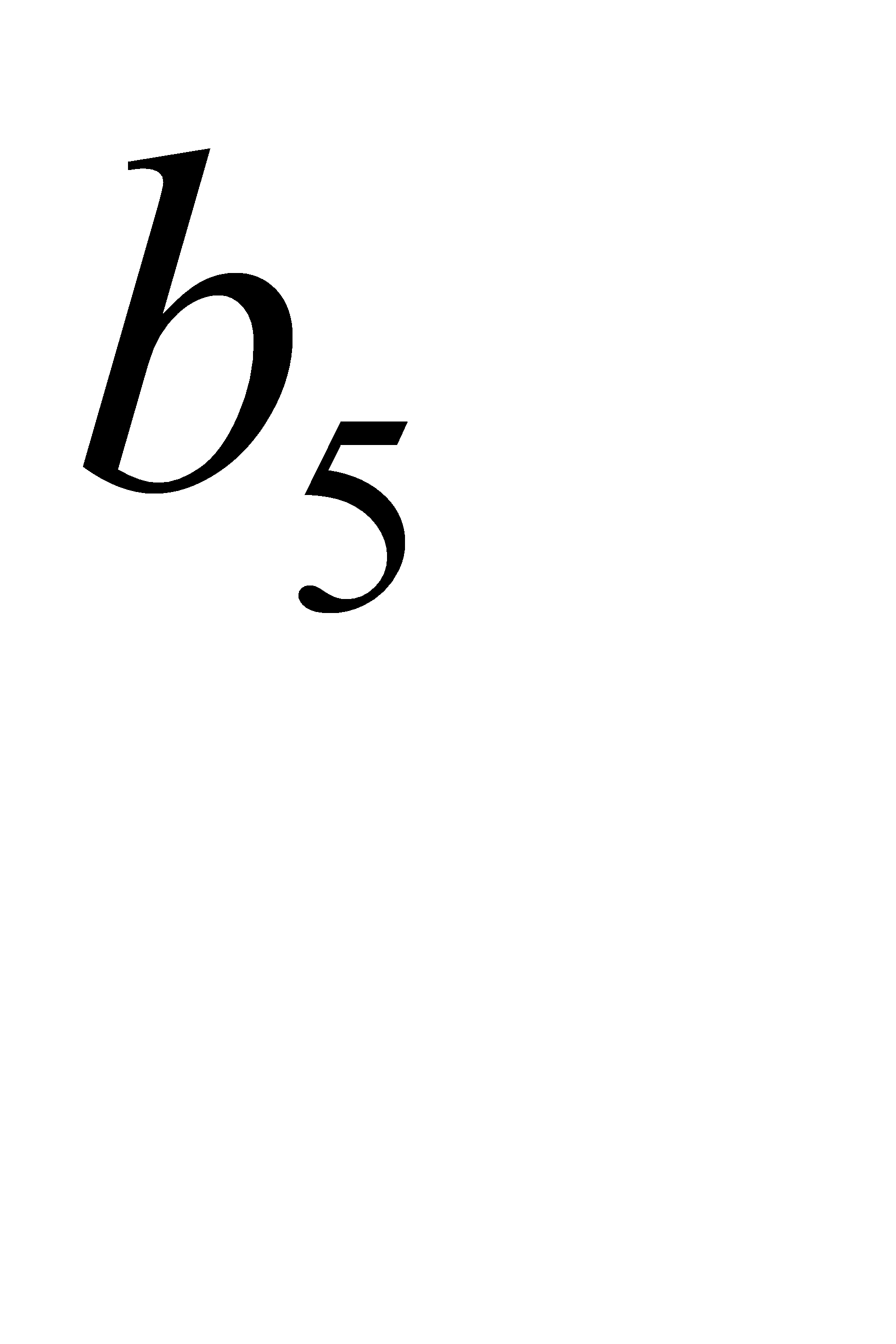
| 0,05 |
|
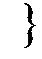
| 1 | 1 | 1 | 1 | 0 | |||
|
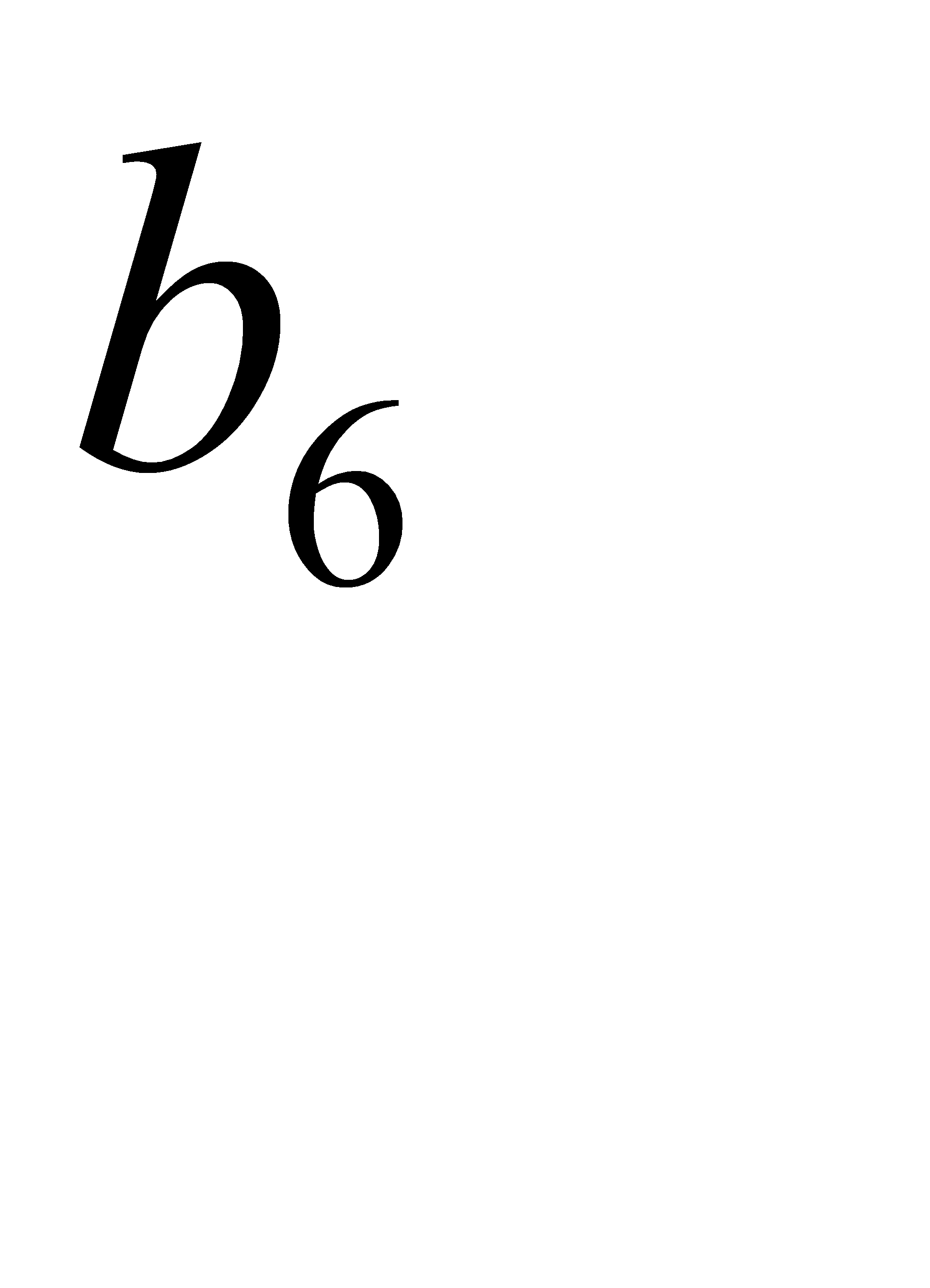
| 0,05 |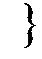
| 1 | 1 | 1 | 1 | 1 | ||||
Алгоритм Шеннона (1948)
Рассмотрим алфавит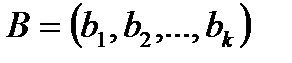 
с заданным распределением вероятностей 
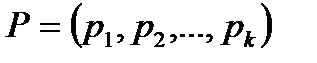. Алгоритм Шеннона применяется лишь в случае, когда в данном распределении все вероятности 
, 
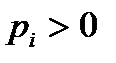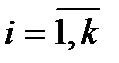. Каждому символу алфавита 
, 
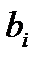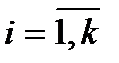, ставится в соответствие значение
, .
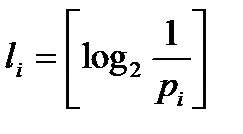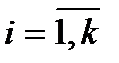Получается последовательность двоичных символов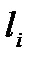 
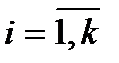, , которые удовлетворяют неравенству Мак-Миллана. После определения этих значений применяется описанные ранее алгоритм Шеннона построения схемы кодирования по заданному набору длин элементарных кодов.
Пример. Построить код, используя алгоритм Шеннона, для алфавита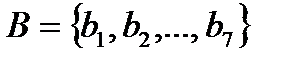 
с заданным распределением вероятностей .
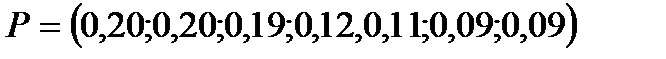Вычислим наборы длин элементарных кодов:
, 
, 
, 
, 
.
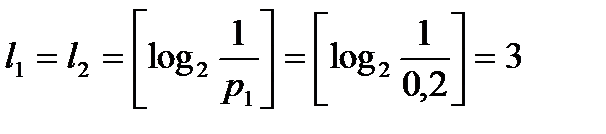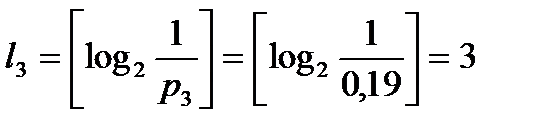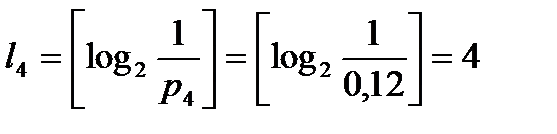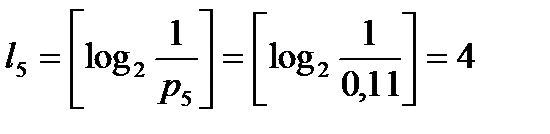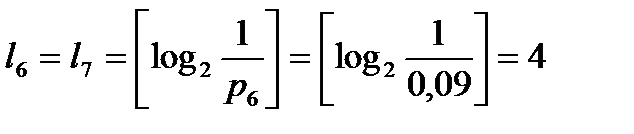Здесь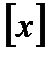 
- ближайшее сверху значение х. Например, 
, 
.
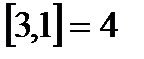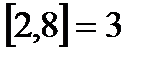Очевидно, что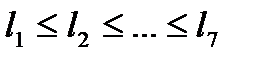 
, причем 
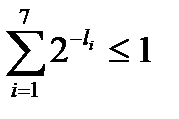. Построим префиксный код по алгоритму Шеннона, используя заданные длины элементарных кодов. Вычислим вспомогательную последовательность чисел 
, 
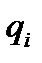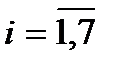, записывая их в двоичной системе счисления, по формуле:
, 
, 
.
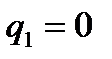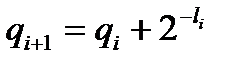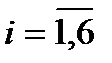Получаем
, 
, 
, 
, 
, 
, 
.
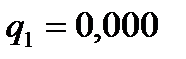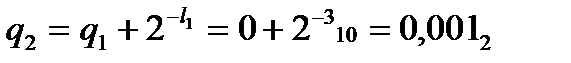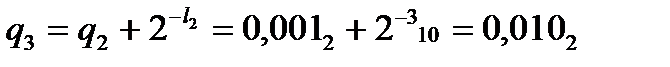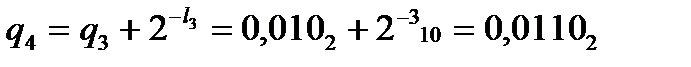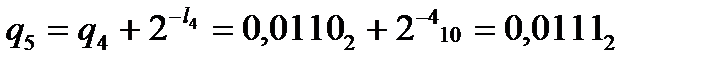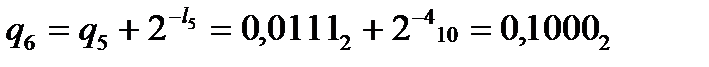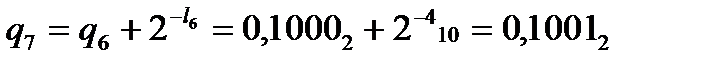Строим схему алфавитного кодирования, выбирая в качестве элементарных кодов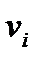 
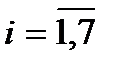, , последовательность из 0 и 1, заданной длины, образующих дробную часть двоичной записи элементов 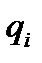, 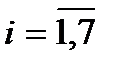. Напомним, что недостающие разряды в записи дополняются справа нулями.
Получаем
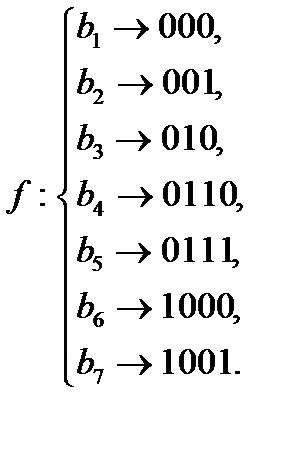
Стоимость кодирования равна
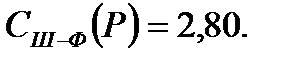
Известно, что при объединении зависимых систем суммарная энтропия меньше суммы энтропий отдельных систем. Следовательно, информация, передаваемая отрезком связанного текста, всегда меньше, чем информация на один символ, умноженная на число символов. Поэтому более экономичный код можно построить, если кодировать не каждую букву в отдельности, а целые «блоки» из букв. Например, «тся», «ает», «ние» и т. д.
Кодируемые блоки располагаются в порядке убывания частот и двоичное кодирование осуществляется по тому же принципу.
Пример. Определить среднюю длину кодовой комбинации при эффективном кодировании по методу Шеннона - Фано ансамбля - из восьми знаков и энтропию алфавита.
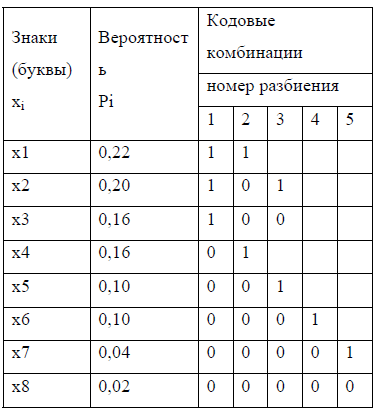
Средняя длина кодовых комбинаций – 2,84. Энтропия алфавита Н=2,76. При кодировании по методу Шеннона - Фано некоторая избыточность в последовательностях символов, как правило, остается (qср > H). Эту избыточность можно устранить, если перейти к кодированию достаточно большими блоками.
Дата добавления: 2021-07-19; просмотров: 471; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!