ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

Цель и задачи работы

Научиться производить проверку статистических гипотез.

 

Порядок выполнения работы

- ознакомится с теоретическими сведениями;

- выполнить задание;

- оформить отчет;

- ответить на контрольные вопросы, заданные преподавателем.

 

Оформление отчета

Отчет должен содержать: титульный лист, цель работы, описание пунктов выполнения лабораторной работы в соответствии с заданием, ответы на контрольные вопросы и выводы по работе.

 

Теоретические сведения

Статистической гипотезой называют гипотезу о виде неизвестного распределения генеральной совокупности или о параметрах известных распределений.

Нулевой (основной) называют выдвинутую гипотезу Н₀. Конкурирующей (альтернативной) называют гипотезу Н1, которая противоречит нулевой.

Пример. Пусть Н₀ заключается в том, что математическое ожидание генеральной совокупности а=3. Тогда возможные варианты Н1: а) а ≠ 3; б) а > 3; в) а < 3.

Проверка гипотез

Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Эту величину называют статистическим критерием K. Для проверки гипотезы по данным выборок вычисляют точные значения входящих в критерий величин и таким образом получают наблюдаемое значение критерия K_набл.

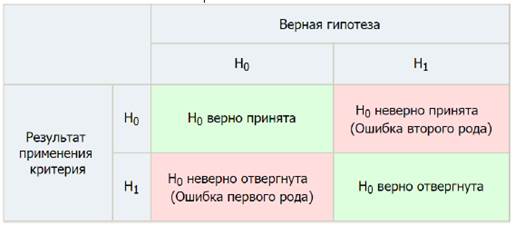
После выбора определенного критерия множество всех его возможных значений разбивают два непересекающихся подмножества: W, содержащее значения критерия, при которых H₀ принимается – область принятия гипотезы, и W – при которых нулевая гипотеза H₀ отвергается, – критическая область. При использовании любого критерия возможны ошибки следующих видов:

1) ошибка первого рода – принять гипотезу H₁, когда верна H₀;

2) ошибка второго рода – принять гипотезу H₀, когда верна H1.

Для каждой из них могут быть заданы соответствующие вероятности:

 

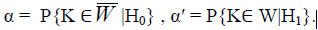
Вероятность ошибки первого рода называется критерием (или уровнем) значимости. Нулевую гипотезу отвергают, если для нее значение p ниже уровня значимости, т. е., если p<α. Обычно назначают условное значение 0,05, тогда шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α=0,05, так как нулевую гипотезу отвергают только тогда, когда p<0,05. Если обнаружено, что p>0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода. Величина (1-β) называется мощностью критерия.

 

Односторонние и двусторонние критические области.

Точки, отделяющие критическую область от области принятия гипотезы называют критическими точками k_кр. Различают одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области:

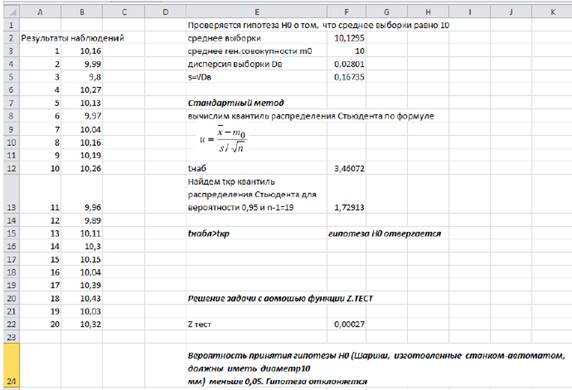
1. Правосторонняя критическая область определяется неравенством K>k_кр, где k_кр>0. Например, когда проверяется гипотеза о том, что среднее значение равно 10.

2. Левосторонняя критическая область K<k_кр, где k_кр<0 .

3. Двусторонняя критическая область K< k₁, K>k₂, где k₂>k₁. В частности, если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется как |K |> k_кр.

Для нахождения критической точки k_кр правосторонней критической области при условии, что справедлива гипотеза H₀:

1) задаются достаточно малой вероятностью — уровнем значимости α (связанной с доверительной вероятностью β соотношением α=1− β);

2) ищут k_кр, исходя из требования: P (K >k_кр=α);

3) по таблицам соответствующих критериев находят k кр и сравнивают с наблюдаемым значением критерия K_набл;

4) если K_набл > k_кр, то H₀ отвергают; если K_набл < k_кр , нет оснований отвергать H₀.

Отыскание левосторонней и двусторонней критических областей сводится к нахождению соответствующих критических точек:

P(K< k_кр)= α – требование для левосторонней критической области;

P(K<k₁)+P(K>k₂)=α – требование для двусторонней критической области.

Если выбрать симметричные относительно нуля точки: −k_кр и k_кр (k_кр>0), то получим следующее соотношение для отыскания критических точек двусторонней области:

Для пересчета одностороннего значения уровня значимости в двустороннее значение можно воспользоваться простой формулой: α_{двустор}=2 ⋅ α_{одностор}.

Существенным моментом является то, что статистические методы не позволяют подтвердить гипотезу. Корректное утверждение, которое можно сформулировать в результате анализа, звучит, например: «проведенный анализ не позволяет с заданным уровнем значимости отвергнуть гипотезу».

Проверить гипотезу о равенстве среднего значения заданному можно двумя способами.

Первый способ:

Пусть генеральная совокупность Х имеет нормальное распределение, и требуется проверить предположение о том, что ее математическое ожидание равно некоторому числу m₀. Рассмотрим две возможности.

1) Известна дисперсия σ² генеральной совокупности. Тогда по выборке объема n найдем выборочное среднее x и проверим нулевую гипотезу Н₀: М(Х)=m₀. Критерием может служить величина

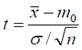
где t – квантиль нормального распределения. Если же дисперсия неизвестна, то используется статистика

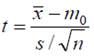
имеющая распределение Стъюдента с (n–1) степенью свободы, t – квантиль распределения Стьюдента, s – среднее квадратическое отклонение выборки.

Найденное значение t сравнивается с критическим t_кр, которое определяется по таблице квантилей в зависимости от уровня значимости или вычисляется встроенными функциями Excel. При попадании выборочного значения в критическую область гипотеза отвергается.

Второй способ:

Для проверки гипотезы о равенстве среднего заданному значению может быть использована функция Z.ТЕСТ, которая вычисляет двухстороннюю вероятность значений z-теста при стандартном распределении.

Синтаксис:

Z.ТЕСТ (Данные; Число; Сигма)

Данные: массив данных.

Число: значение для теста.

Сигма: необязательное стандартное отклонение генеральной совокупности. Если аргумент не указан, используется стандартное отклонение выборки.

Пример:

=Z.ТЕСТ (A1:A50; 12) вычисляет вероятность того, что значение12 относится к стандартному распределению генеральной совокупности данных в A1:A50.

При использовании этой функции вычисляется вероятность того, что для генеральной совокупности справедлива гипотеза H₀: m=m₀. Используется двухсторонний критерий, то есть альтернативная гипотеза H₁: m≠m₀. Если эта вероятность меньше заданного уровня значимости, гипотеза отклоняется.

 

 

 

Проверка гипотез о равенстве дисперсий

При проверке гипотеза о равенстве дисперсий двух нормально распределенных совокупностей Н0: σ₁²=σ₂² при неизвестных математических ожиданиях m₁ и m₂ используется статистика

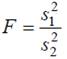                                               (1)

которая имеет F-распределение Фишера с числом степеней свободы (n₁–1) и (n₂–1); здесь n₁ и n₂ – объемы выборок, s₁² и s₂² – соответствующие несмещенные дисперсии; при этом предполагается, что s₁² > s₂².

Для проверки этой гипотезы в Excel есть функция F.ТЕСТ, которая возвращает результат F-теста. Синтаксис функции:

F.ТЕСТ (Данные1; Данные2)

Данные1: первый массив записей.

Данные2: второй массив записей.

Пример:

=F.ТЕСТ (A1:A30; B1:B12) вычисляет различие дисперсий для двух множеств данных и возвращает вероятность того, что оба множества представляют собой выборку из общей совокупности.

 

Проверка гипотез о виде распределения

Другой группой статистических гипотез являются гипотезы о проверке вида распределения: неизвестен вид распределения генеральной совокупности, и в частности, неизвестна функция распределения F(x).

Пусть x₁,x₂,…,x_n – выборка наблюдений случайной величины X. Проверяется гипотеза Н₀ о том, что случайная величина X имеет функцию распределения F(x). Разобьем область возможных значений X на r интервалов Δ₁, Δ₂, … Δ_r. Пусть n_i – число элементов выборки, принадлежащих интервалу Δ_i(i=1, …, r); при малых значениях n_i интервалы объединяют таким образом, чтобы в каждом из них было n_i≥5. Используя предполагаемый закон распределения – с функцией F(x), c учетом оценок параметров этого закона, найденных по выборке, находят вероятности того, что значения X принадлежат интервалу Δ_i, то есть

Статистика

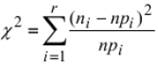
имеет распределение χ² с числом степеней свободы (r–l–1), где r – число интервалов, l – число неизвестных параметров распределения. Например, для нормального распределения l=2 (неизвестные параметры m и σ). Считается, что гипотеза Н₀ согласуется с опытом, если

,

где χ² – выборочное значение статистики, 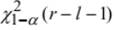 – квантиль порядка (1–α) распределения χ² c числом степеней свободы (r–l–1). Рассмотренный метод проверки гипотезы вида распределения называется критерием хи-квадрат или критерием согласия Пирсона.

 

 

 

Оборудование

Персональный компьютер с установленной операционной системой Windows XP/7/8, браузер (Например, Internet Explorer, Google Chrome, Opera), OOo Writer (MS Word), Ооо Calc (MS Excel) пакет офисных приложений «Мой офис».

 

Задание на работу

1. Шарики, изготовленные станком-автоматом, должны иметь диаметр 10 мм; проверить эту гипотезу по заданной выборке на уровне значимости 0.05, если:

A) Дисперсия известна и равна 0,1 мм²

B) Дисперсия неизвестна.

Результаты наблюдений приведены в таблице.

10,16	9,99	9,8	10,27	10,13	9,97	10,04	10,16	10,19	10,26
9,96	9,89	10,11	10,3	10,15	10,04	10,39	10,43	10,03	10,32

Воспользоваться стандартным алгоритмом проверки гипотез и встроенной функцией Z.ТЕСТ.

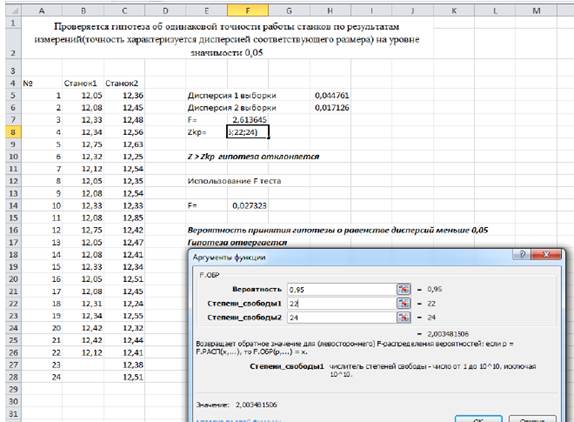
2. Проверить гипотезу об одинаковой точности работы станков по результатам измерений (точность характеризуется дисперсией соответствующего размера) на уровне значимости 0,05 с использованием формулы (1) и функции F.ТЕСТ. Результаты измерений контролируемого параметра на двух станках приведены в таблице.

 

№	Станок1	Станок2	№	Станок1	Станок2
1	12,05	12,36	13	12,05	12,47
2	12,08	12,45	14	12,08	12,41
3	12,33	12,48	15	12,33	12,34
4	12,34	12,56	16	12,05	12,51
5	12,75	12,63	17	12,08	12,45
6	12,32	12,25	18	12,31	12,24
7	12,12	12,54	19	12,34	12,55
8	12,05	12,35	20	12,42	12,32
9	12,08	12,54	21	12,42	12,44
10	12,33	12,33	22	12,12	12,41
11	12,08	12,85	23		12,38
12	12,75	12,42	24		12,51

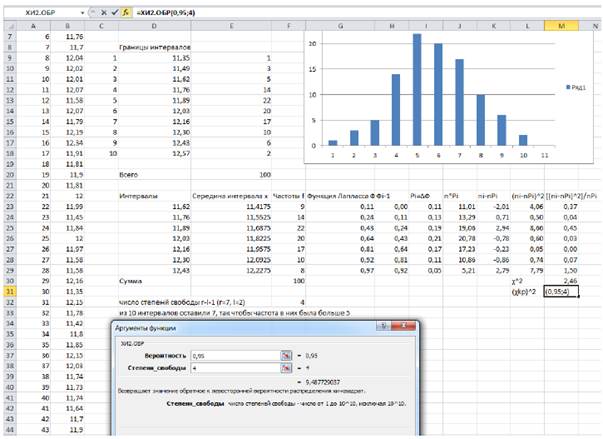
3. Дана выборка из 100 наблюдений; определить числовые характеристики, построить гистограмму частот, проверить нормальность распределения по критерию хи-квадрат.

12,01	12	11,64	12,09	11,79
11,64	11,99	11,7	11,79	12,16
11,59	11,45	11,9	11,86	12,25
11,4	11,84	12,15	11,79	11,92
12,37	12	11,93	11,98	11,72
11,76	11,97	12,25	11,76	11,9
11,7	11,58	12,1	12,39	11,74
12,04	11,58	11,81	12,13	12,09
12,02	12,16	11,94	12,2	11,66
12,01	11,35	12,2	11,84	11,84
12,07	12,15	12,1	11,52	11,84
11,58	11,78	11,79	11,78	11,83
12,07	11,42	12,08	12,03	12,03
11,79	11,8	12,7	11,65	11,96
12,19	11,85	12,42	11,72	12,4
12,34	12,15	11,65	12,27	11,81
11,91	12,03	12,16	12,11	11,92

 

Для выполнения задания необходимо рассчитать и внести в таблицу следующие данные:

n_i – частота попаданий элементов выборки в i-й интервал;

x_i – верхняя граница i-го интервала;

F(x_i) – значение функции нормального распределения;

Δ F_i – теоретическое значение вероятности попадания случайной величины в i-й интервал

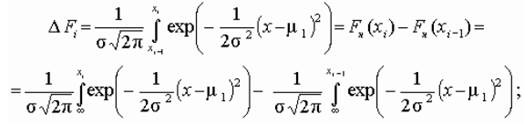
F_i=ΔF_i*n – теоретическая частота попадания случайной величины в i-й интервал; (n_i – F_i)2/F_i – взвешенный квадрат отклонения.

 

Контрольные вопросы

1. Что называется критерием, уровнем значимости, критической областью и областью допустимых значений критерия?

2. Что такое ошибки первого и второго рода?

3. Что называется мощностью критерия?

4. Сформулируйте этапы проверки статистических гипотез.

5. Проверку какой гипотезы осуществляет функция Excel Z.TEST?

 

---

Дата добавления: 2021-07-19; просмотров: 193; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!