В ЛЕГИРОВАННЫХ ГЕТЕРОСТРУКТУРАХ
Одним из важных методов управления электронными свойствами гетероструктур является целенаправленное легирование составляющих структуру материалов донорными или акцепторными примесями. Рассмотрят кратко особенности энергетической диаграммы гетероструктуры, изготовленной с применением метода модулированного легирования. Этот метод позволяет в процессе выращивания структуры внедрять примесные атомы (пусть здесь речь идёт о донорах) только в область потенциальных барьеров [6, 7]. При этом область потенциальной ямы, в которой за счет легирования образуются свободные носители заряда, остаётся почти свободной от дефектов, в результате чего подвижность носителей заряда в ней существенно повышается.
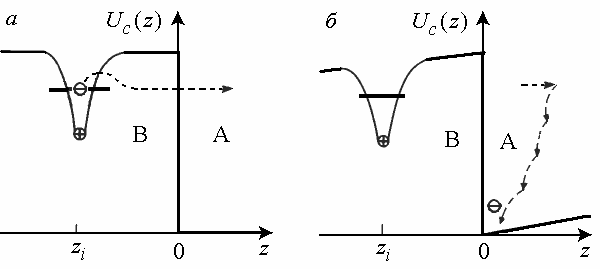
Рисунке 6. Механизм перераспределения электрического заряда в одиночном гетеропереходе. (рис. из книги [https://elib.spbstu.ru/dl/2375.pdf/download/2375.pdf].
Область барьера (материал В) легирована донорной примесью. В области А, начиная от дна зоны проводимости и выше, существует континуум электронных состояний. а – донорный центр переходит из электрически нейтрального состояния в ионизованное, положительно заряженное состояние за счёт перемещения электрона в область А, свободную от примесей. б – электрон, переместившийся в область А из области В, испускает фононы и заселяет свободное состояние с энергией меньшей, чем энергия донорного уровня в материале В. Электрическое поле положительно заряженных ионов в области барьера приводит к изгибу краёв зон
|
|
|
На рисунке 6 схематично показано механизм образования свободных электронов вблизи интерфейса одиночного гетероперехода В / А с селективным легированием. В этом примере материал В с более высоким положением края зоны проводимости 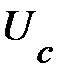 (широкозонный полупроводник) легирован донорной примесью, а материал А (узкозонный полупроводник) примесей не содержит. Если бы доноры оставались в нейтральном состоянии, то химический потенциал электронов в области В был бы выше, чем в области А, что не отвечало бы состоянию термодинамического равновесия. В равновесном состоянии уровень химического потенциала электронов должен быть постоянным по всей системе. Термодинамическое равновесие устанавливается в результате переходов электронов из области В, с донорных центров, в свободные состояния зоны проводимости области А. Переходы осуществляются посредством туннельного эффекта или термоактивационным способом – за счёт взаимодействия с тепловыми колебаниями кристаллической решётки. Поскольку ионизованные доноры заряжены положительно, они притягивают к себе электроны, так что свободные электроны скапливаются в области А вблизи границы с областью В. Это означает, что для электронов в области А образуется потенциальная яма, которую можно представить как следствие изгиба зон.
(широкозонный полупроводник) легирован донорной примесью, а материал А (узкозонный полупроводник) примесей не содержит. Если бы доноры оставались в нейтральном состоянии, то химический потенциал электронов в области В был бы выше, чем в области А, что не отвечало бы состоянию термодинамического равновесия. В равновесном состоянии уровень химического потенциала электронов должен быть постоянным по всей системе. Термодинамическое равновесие устанавливается в результате переходов электронов из области В, с донорных центров, в свободные состояния зоны проводимости области А. Переходы осуществляются посредством туннельного эффекта или термоактивационным способом – за счёт взаимодействия с тепловыми колебаниями кристаллической решётки. Поскольку ионизованные доноры заряжены положительно, они притягивают к себе электроны, так что свободные электроны скапливаются в области А вблизи границы с областью В. Это означает, что для электронов в области А образуется потенциальная яма, которую можно представить как следствие изгиба зон.
|
|
|
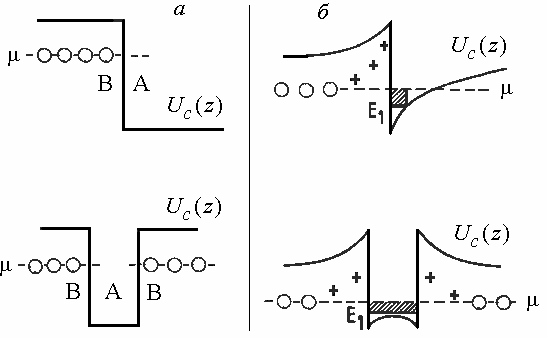
Рисунке 7. Образование двумерного электронного газа в одиночной и в двойной гетероструктурах (рис. из книги [https://elib.spbstu.ru/dl/2375.pdf/download/2375.pdf].
Верхний рисунок – одиночный гетеропереход, нижний рисунок – двойная гетероструктура с квантовой ямой. а – неравновесное состояние, все доноры электронейтральны. б – равновесное состояние. Белые кружки изображают доноры в нейтральном состоянии, крестики – положительно заряженные (ионизованные) донорные центры. Штриховкой показан двумерный электронный газ, частично заполняющий состояния размерно-квантованной подзоны  .
.
Такая потенциальная яма вблизи границы В / А имеет форму, напоминающую треугольную, и в ней может образоваться одна или несколько размерно-квантованных подзон 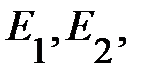 … . Свободные электроны, появившиеся в области А за счет переходов с доноров из области В, заселяют состояния подзон, тем самым образуя двумерный электронный газ. В двойном гетеропереходе, представляющем для электронов квантовую яму В / А / В, размерно-квантованные состояния существуют уже в отсутствие легирования, но при этом они не заселены электронами. Легирование В-слоёв донорной примесью позволяет получить двумерный электронный газ также и в этом случае (см. рисунке 7).
… . Свободные электроны, появившиеся в области А за счет переходов с доноров из области В, заселяют состояния подзон, тем самым образуя двумерный электронный газ. В двойном гетеропереходе, представляющем для электронов квантовую яму В / А / В, размерно-квантованные состояния существуют уже в отсутствие легирования, но при этом они не заселены электронами. Легирование В-слоёв донорной примесью позволяет получить двумерный электронный газ также и в этом случае (см. рисунке 7).
|
|
|
Особенностью рассмотренной картины является то, что для количественного анализа изгиба зон и положения уровней размерного квантования здесь необходимы самосогласованные расчёты – совместное решение уравнения Шредингера и уравнений электростатики, определяющих потенциальный рельеф 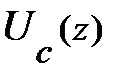 .
.
2. 1 Энергетический спектр 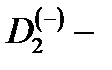 центра в квантовой проволоке:
центра в квантовой проволоке:
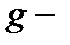 и
и  термы
термы
Как показывают эксперименты [12], в низкоразмерных системах при определенных условиях возможны реакции типа  , в результате которых нейтральные мелкие доноры связывают дополнительный электрон с образованием популяции, так называемых
, в результате которых нейтральные мелкие доноры связывают дополнительный электрон с образованием популяции, так называемых 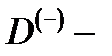 состояний. Такие состояния, ограниченные потенциалом конфайнмента, открывают новые возможности для изучения корреляционных эффектов в низкоразмерных системах [12]. В настоящей работе рассмотрена ситуация, когда не все
состояний. Такие состояния, ограниченные потенциалом конфайнмента, открывают новые возможности для изучения корреляционных эффектов в низкоразмерных системах [12]. В настоящей работе рассмотрена ситуация, когда не все 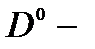 позиции могут эффективно заполняться электронным переносом из барьера. В этом случае, в зависимости от расстояния
позиции могут эффективно заполняться электронным переносом из барьера. В этом случае, в зависимости от расстояния 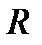 между
между 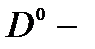 центрами, возможно образование отрицательного молекулярного иона
центрами, возможно образование отрицательного молекулярного иона 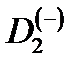 . Следует отметить, что система, состоящая из слабосвязанного электрона в поле двух одинаковых потенциальных центров, встречается также и в щелочно-галоидных кристаллах [77]. Это так называемый
. Следует отметить, что система, состоящая из слабосвязанного электрона в поле двух одинаковых потенциальных центров, встречается также и в щелочно-галоидных кристаллах [77]. Это так называемый 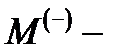 центр окраски, который представляет собой электрон в поле нейтрального
центр окраски, который представляет собой электрон в поле нейтрального 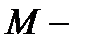 центра (два рядом расположенных
центра (два рядом расположенных 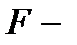 центра). Как известно [78,79],
центра). Как известно [78,79],  центр является простейшей системой, которая может моделироваться электроном в поле потенциала нулевого радиуса. Ранее [8,9] было показано, что метод потенциала нулевого радиуса позволяет получить аналитическое решение для волновой функции и энергии связи локализованного на
центр является простейшей системой, которая может моделироваться электроном в поле потенциала нулевого радиуса. Ранее [8,9] было показано, что метод потенциала нулевого радиуса позволяет получить аналитическое решение для волновой функции и энергии связи локализованного на 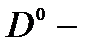 центре электрона, а также исследовать примесное магнитопоглощение света в КП с параболическим потенциалом конфайнмента. Моделирование отрицательного молекулярного иона
центре электрона, а также исследовать примесное магнитопоглощение света в КП с параболическим потенциалом конфайнмента. Моделирование отрицательного молекулярного иона 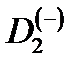 и исследование его магнитооптических свойств в КП представляет отдельный интерес. Так как
и исследование его магнитооптических свойств в КП представляет отдельный интерес. Так как 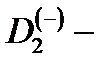 система является симметричной относительно ее центра, состояния электрона при фиксированном расстоянии
система является симметричной относительно ее центра, состояния электрона при фиксированном расстоянии 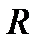 между
между 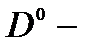 центрами должны быть либо симметричными (
центрами должны быть либо симметричными ( 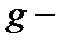 термы), либо антисимметричными (
термы), либо антисимметричными ( 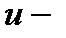 термы). Очевидно, что расщепление
термы). Очевидно, что расщепление 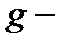 и
и  термов (вырожденных при больших
термов (вырожденных при больших 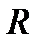 ) будет определяться величиной
) будет определяться величиной 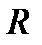 и, как следствие понижения размерности – параметрами КП. С другой стороны, приложенное вдоль оси КП магнитное поле играет роль варьируемого параметра, посредством которого можно изменять геометрический конфайнмент системы и, следовательно, управлять как величиной расщепления, так и энергиями оптических переходов [8].
и, как следствие понижения размерности – параметрами КП. С другой стороны, приложенное вдоль оси КП магнитное поле играет роль варьируемого параметра, посредством которого можно изменять геометрический конфайнмент системы и, следовательно, управлять как величиной расщепления, так и энергиями оптических переходов [8].
|
|
|
Цель настоящего раздела состоит в том, чтобы в рамках модели потенциала нулевого радиуса проследить за эволюцией термов с изменением величины продольного магнитного поля в КП.
Рассмотрят задачу на связанные состояния электрона, локализованного на 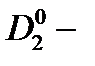 центре в полупроводниковой КП с параболическим потенциалом конфайнмента, помещенной в продольное магнитное поле. Будем считать, что КП имеет форму круглого цилиндра, радиус основания
центре в полупроводниковой КП с параболическим потенциалом конфайнмента, помещенной в продольное магнитное поле. Будем считать, что КП имеет форму круглого цилиндра, радиус основания 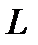 которого значительно меньше его длины
которого значительно меньше его длины 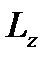 (
( 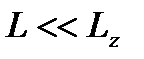 ). Для описания одноэлектронных состояний в КП будем использовать симметричный потенциал конфайнмента вида
). Для описания одноэлектронных состояний в КП будем использовать симметричный потенциал конфайнмента вида
 , (2.1.1)
, (2.1.1)
где 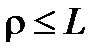 ;
;  – цилиндрические координаты;
– цилиндрические координаты;  – эффективная масса электрона;
– эффективная масса электрона; 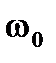 – характерная частота удерживающего потенциала КП.
– характерная частота удерживающего потенциала КП.
Пусть КП находится в продольном по отношению к ее оси магнитном поле с вектором магнитной индукции 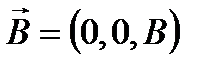 . Векторный потенциал магнитного поля
. Векторный потенциал магнитного поля 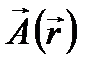 выберем в симметричной калибровке
выберем в симметричной калибровке
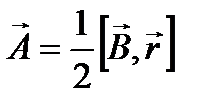 , (2.1.2)
, (2.1.2)
в результате получим, что 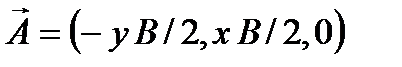 .
.
Для невозмущенных примесями одноэлектронных состояний в продольном магнитном поле гамильтониан в выбранной модели в цилиндрической системе координат имеет вид
 , (2.1.3)
, (2.1.3)
где 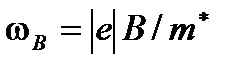 – циклотронная частота;
– циклотронная частота; 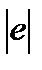 – абсолютное значение электрического заряда электрона;
– абсолютное значение электрического заряда электрона;  .
.
Тогда спектр гамильтониана (2.1.3) запишется как [8]
 , (2.1.4)
, (2.1.4)
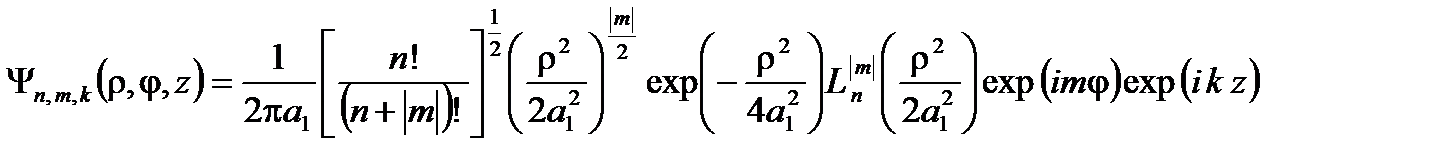 , (2.1.5)
, (2.1.5)
где  – квантовое число, соответствующее уровням Ландау;
– квантовое число, соответствующее уровням Ландау; 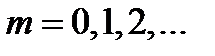 – магнитное квантовое число;
– магнитное квантовое число; 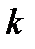 – проекция квазиволнового вектора электрона в КП на ось Oz;
– проекция квазиволнового вектора электрона в КП на ось Oz; 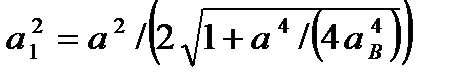 ;
; 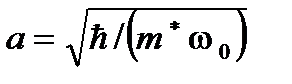 ;
; 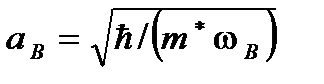 – магнитная длина;
– магнитная длина; 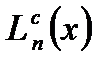 – полиномы Лагерра [17].
– полиномы Лагерра [17].
Пусть 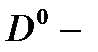 центры расположены в точках
центры расположены в точках 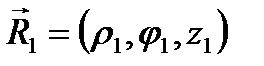 и
и  , здесь
, здесь 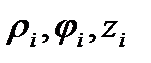
 – цилиндрические координаты примесных центров. Двухцентровой потенциал моделируется суперпозицией потенциалов нулевого радиуса мощностью
– цилиндрические координаты примесных центров. Двухцентровой потенциал моделируется суперпозицией потенциалов нулевого радиуса мощностью 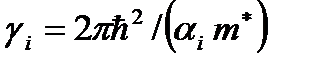 :
:
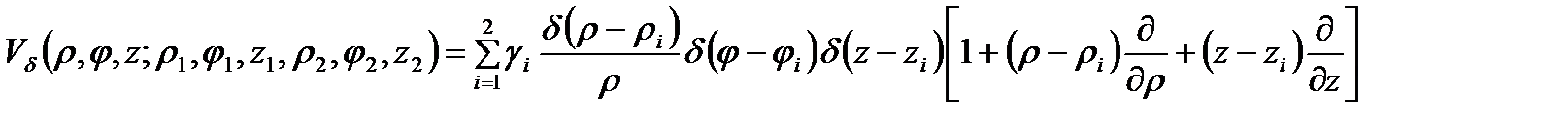 (2.2.6)
(2.2.6)
где 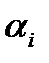 определяется энергией
определяется энергией  связанного состояния на этих же
связанного состояния на этих же  центрах в массивном полупроводнике;
центрах в массивном полупроводнике; 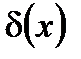 – дельта-функция Дирака.
– дельта-функция Дирака.
В приближении эффективной массы волновая функция электрона  , локализованного на
, локализованного на 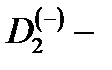 центре, удовлетворяет уравнению Липпмана-Швингера для связанного состояния:
центре, удовлетворяет уравнению Липпмана-Швингера для связанного состояния:
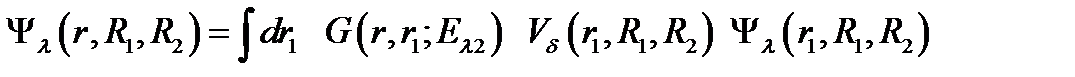 , (2.1.7)
, (2.1.7)
где 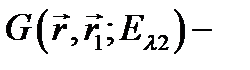 одноэлектронная функция Грина, соответствующая источнику в точке
одноэлектронная функция Грина, соответствующая источнику в точке 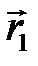 , и энергии
, и энергии  (
( 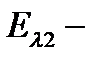 энергия связанного состояния электрона в поле
энергия связанного состояния электрона в поле 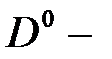 центров при наличии продольного магнитного поля, отсчитываемая от дна двумерной осцилляторной ямы):
центров при наличии продольного магнитного поля, отсчитываемая от дна двумерной осцилляторной ямы):
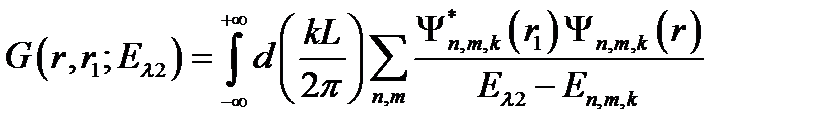 (2.1.8)
(2.1.8)
Подставляя (2.1.6) в (2.1.7), получим
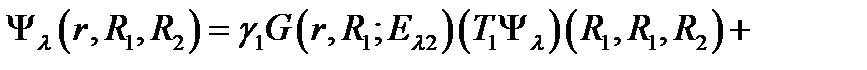

, (2.1.9)
где 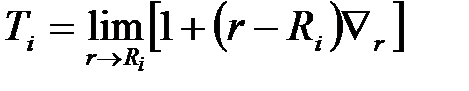 (2.1.10)
(2.1.10)
Применят последовательно операцию (2.1.10) к обеим частям соотношения (2.1.9), получим систему алгебраических уравнений вида [A5, A6]:
 , (2.1.11)
, (2.1.11)
здесь 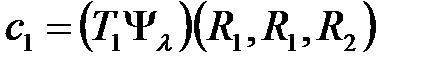 ;
; 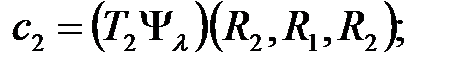
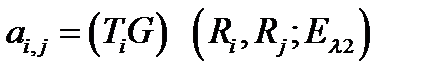 ;
;  .
.
Исключая из системы (2.1.11) коэффициенты  , содержащие неизвестную функцию, получим уравнение, определяющее зависимость энергии связанного состояния
, содержащие неизвестную функцию, получим уравнение, определяющее зависимость энергии связанного состояния  электрона на
электрона на 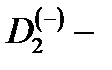 центре от координат
центре от координат 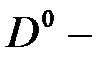 центров, параметров КП и величины магнитного поля:
центров, параметров КП и величины магнитного поля:
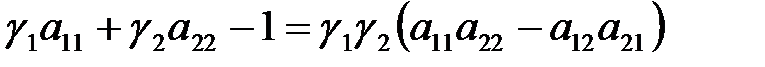 (2.1.12)
(2.1.12)
Таким образом, задача на связанные состояния электрона локализованного на  – центре в полупроводниковой КП с параболическим потенциалом конфайнмента, помещенной в продольное магнитное поле сводится к построению одноэлектронной функции Грина (2.1.8)
– центре в полупроводниковой КП с параболическим потенциалом конфайнмента, помещенной в продольное магнитное поле сводится к построению одноэлектронной функции Грина (2.1.8)
Используют явный вид одночастичных волновых функций (2.1.5), а также (2.1.4), для функции Грина в (2.1.8) будем иметь:
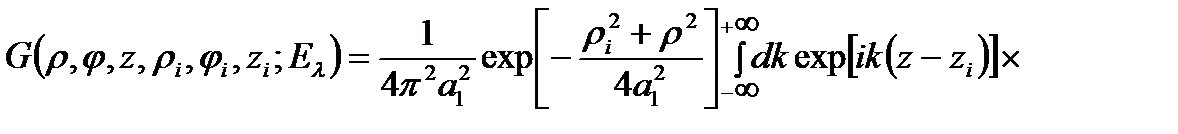
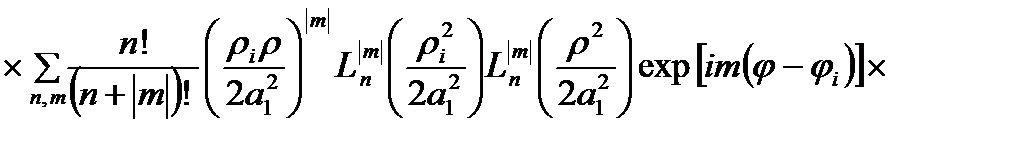
 (2.1.13)
(2.1.13)
Воспользуются очевидным соотношением
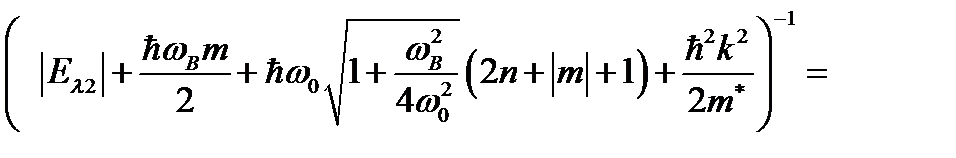
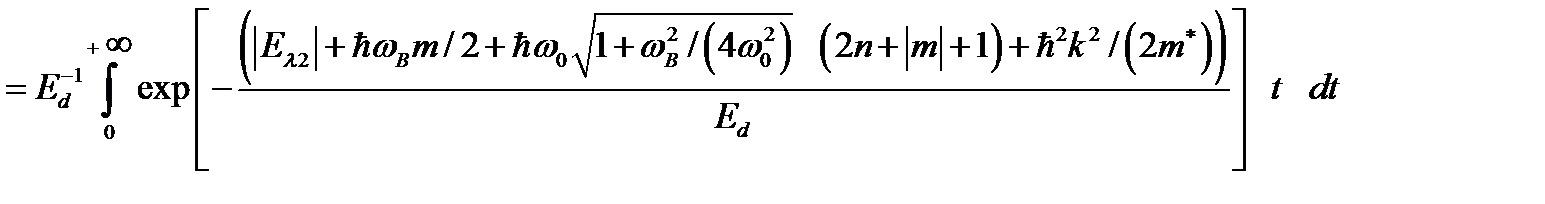 , (2.1.14)
, (2.1.14)
тогда выражение (2.1.13) можно представить в виде
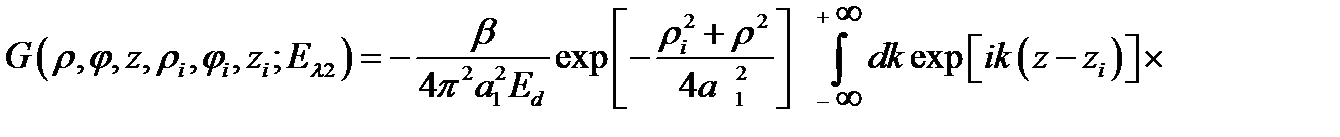
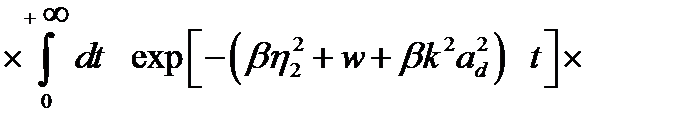
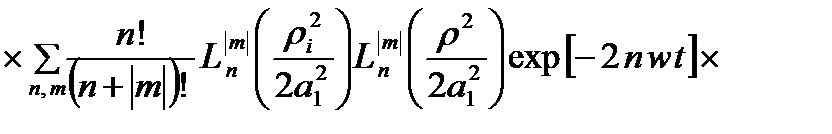
 , (2.1.15)
, (2.1.15)
где 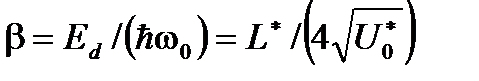 ;
; 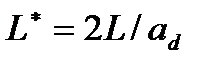 ;
; 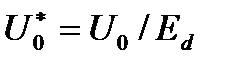 ;
;  ;
; 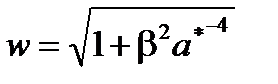 ;
; 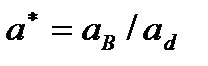 .
.
Используют формулу Хилле-Харди для билинейной производящей функции (подробно это выполнено в пункте 1.1 главы 1), произведем суммирование по квантовым числам 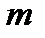 и
и 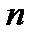 .
.
Следует заметить, что изменение порядка интегрирования в (2.1.15) приводит к интегралу вида
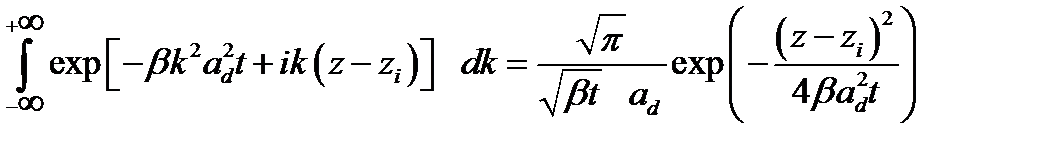 , (2.1.16)
, (2.1.16)
где было учтено, что [17]
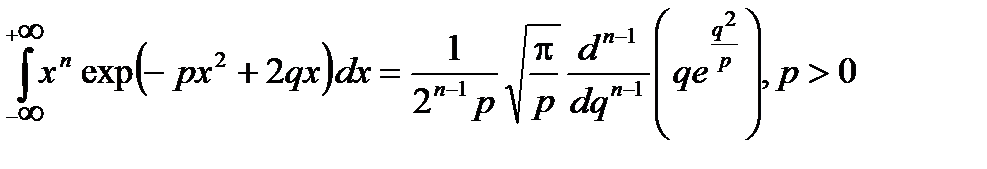 (2.1.17)
(2.1.17)
Далее, учитывая (2.1.16), для функции Грина 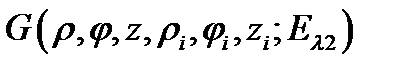 получим
получим
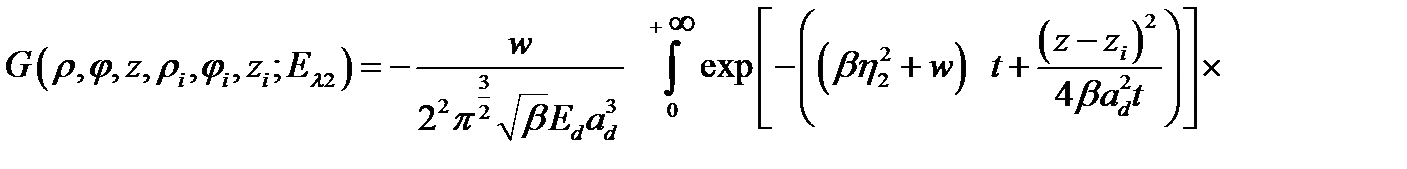
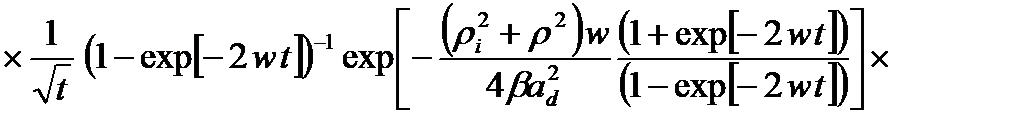
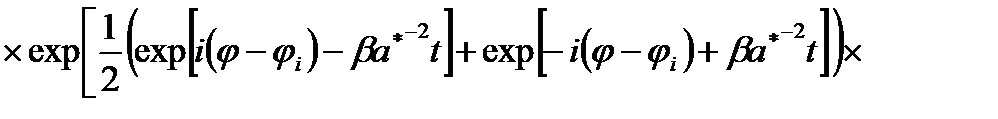
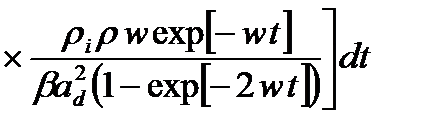 (2.1.18)
(2.1.18)
Для выделения в (2.1.18) расходящейся части воспользуемся интегралом Вебера, который в принятых в этой главе обозначениях имеет вид [17]
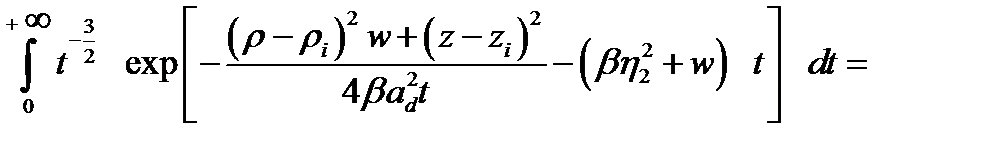
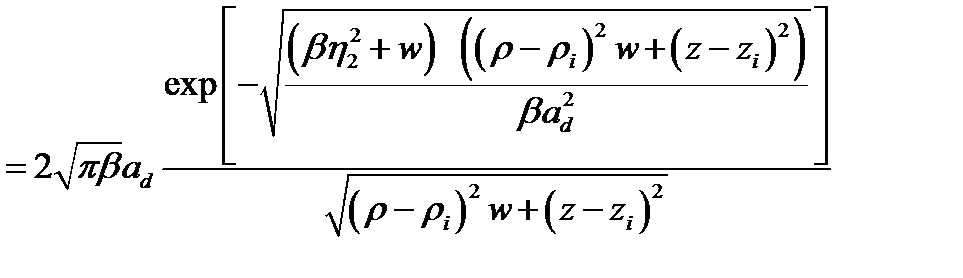 (2.1.19)
(2.1.19)
Тогда выражение (2.1.18) для функции Грина запишется как

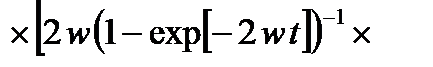
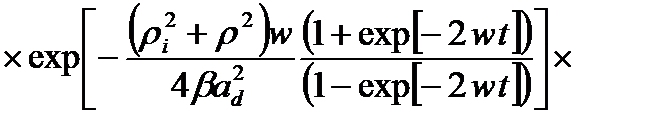
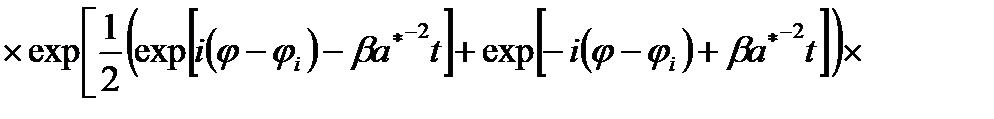
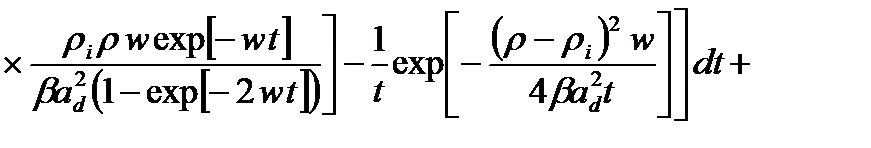
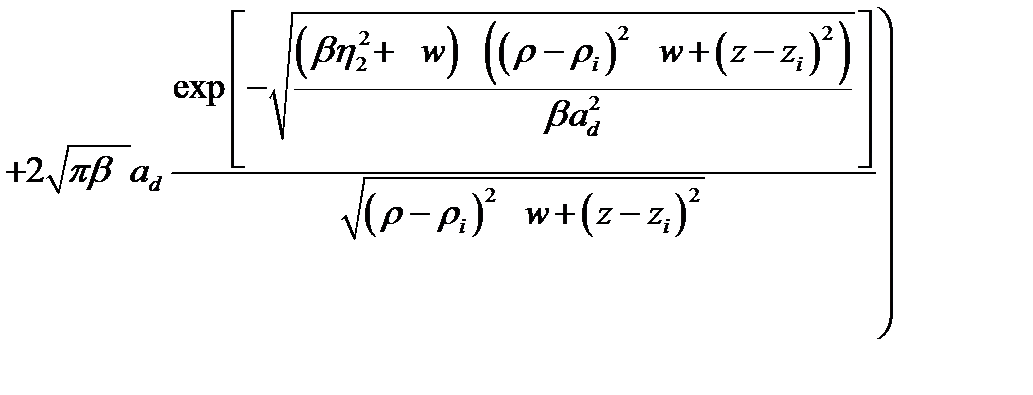 (2.1.20)
(2.1.20)
Коэффициенты 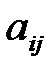 , входящие в (2.1.12), с учетом (2.1.20) примут вид:
, входящие в (2.1.12), с учетом (2.1.20) примут вид:

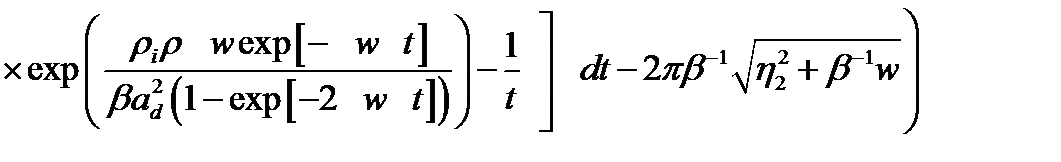 , (2.1.21)
, (2.1.21)


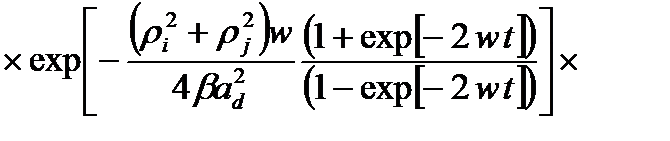
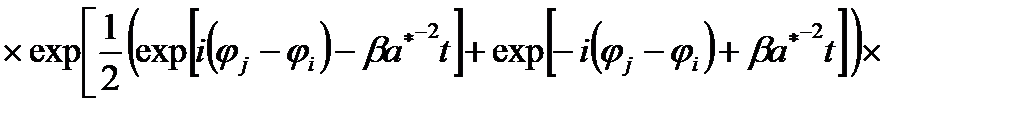
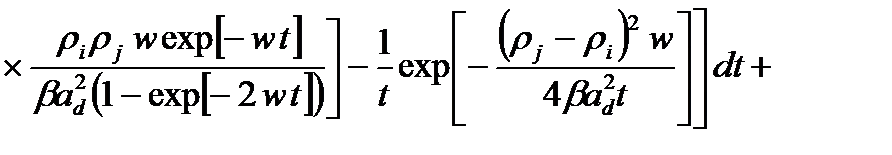
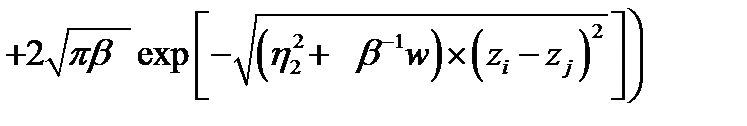 (2.1.22)
(2.1.22)
В случае, когда 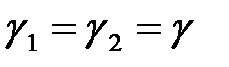 и
и 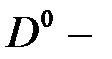 центры расположены на оси КП
центры расположены на оси КП 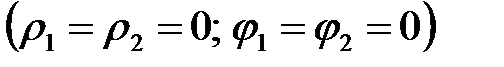 уравнение (2.1.12) распадается на два уравнения, определяющих симметричное (
уравнение (2.1.12) распадается на два уравнения, определяющих симметричное ( 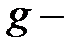 терм) и антисимметричное (
терм) и антисимметричное ( 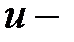 терм) состояния электрона соответственно:
терм) состояния электрона соответственно:
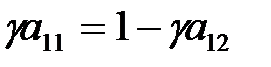 ,
, 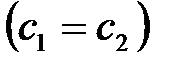 (2.1.23)
(2.1.23)
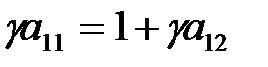 ,
, 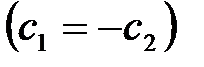 , (2.1.24)
, (2.1.24)
где
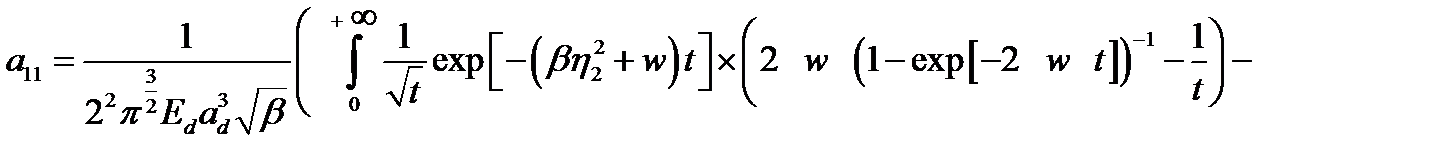
 , (2.1.25)
, (2.1.25)


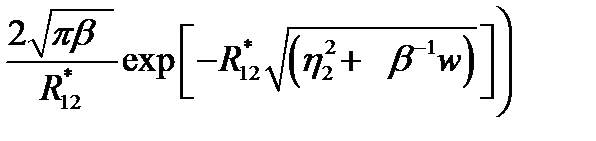 , (2.1.26)
, (2.1.26)
где 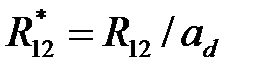 ;
; 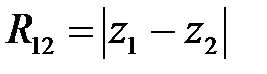 – расстояние между
– расстояние между 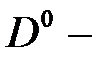 центрами.
центрами.
Подставляют выражения (2.1.25), (2.1.26) в (2.1.23) и (2.1.24) получили уравнения, определяющие зависимости энергии связанного состояния электрона в симметричном 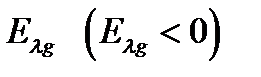 и антисимметричном
и антисимметричном 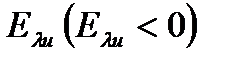 состояниях от расстояния между
состояниях от расстояния между 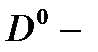 центрами, от параметров КП и величины магнитной индукции [A1, A5, A6]:
центрами, от параметров КП и величины магнитной индукции [A1, A5, A6]:

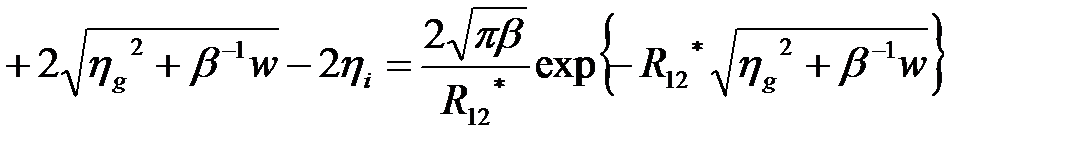 (2.1.27)
(2.1.27)
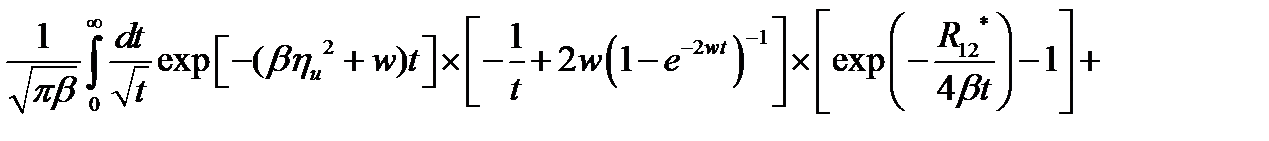
 , (2.1.28)
, (2.1.28)
где  ,
, 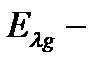 энергия связи соответствующая
энергия связи соответствующая 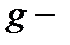 терму;
терму;  ,
, 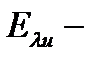 энергия связи соответствующая
энергия связи соответствующая  терму.
терму.
Рассмотрят случай, когда примесный уровень 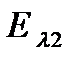 расположен между дном двумерной осцилляторной потенциальной ямы, которой описывается потенциал КП, и уровнем энергии основного состояния
расположен между дном двумерной осцилляторной потенциальной ямы, которой описывается потенциал КП, и уровнем энергии основного состояния 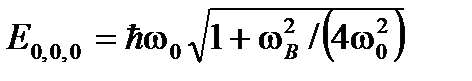 электрона в КП:
электрона в КП: 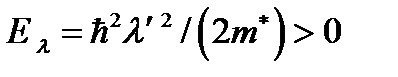 . Замена
. Замена 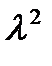 на
на 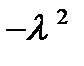 или
или 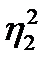 на
на 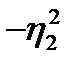 приводит к переходу от случая
приводит к переходу от случая 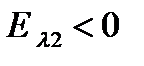 к случаю
к случаю 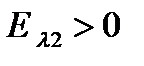 . Тогда трансцендентные уравнения, определяющие зависимости энергии связанного состояния электрона в симметричном
. Тогда трансцендентные уравнения, определяющие зависимости энергии связанного состояния электрона в симметричном 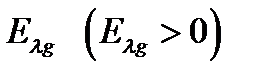 и антисимметричном
и антисимметричном 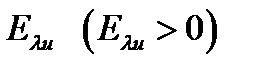 состояниях от расстояния между
состояниях от расстояния между 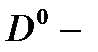 центрами, от параметров КП и величины магнитной индукции, примут вид:
центрами, от параметров КП и величины магнитной индукции, примут вид:
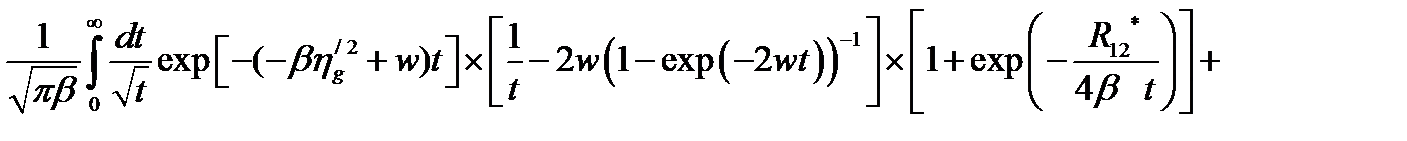
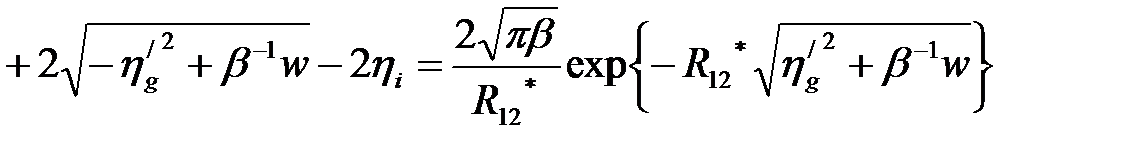 (2.1.29)
(2.1.29)
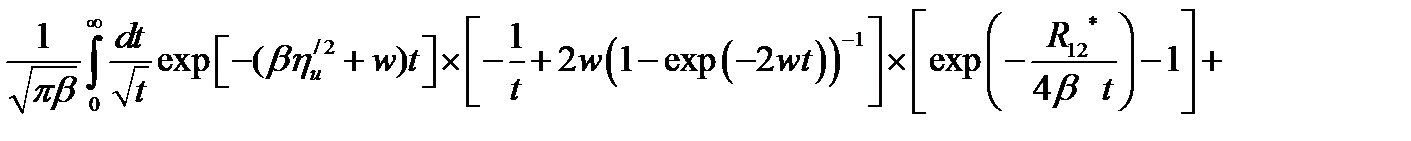
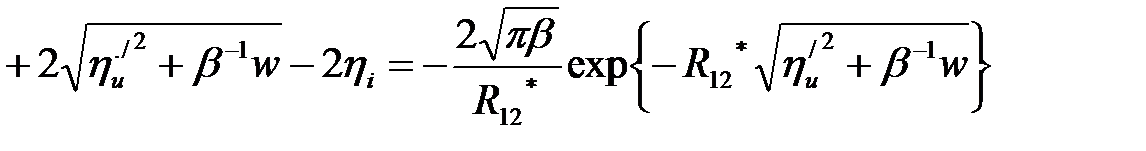 (2.1.30)
(2.1.30)
Из-за наличия квантового размерного эффекта энергию связи электрона локализованного на двух 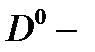 центрах в КП, помещенной в продольное магнитное поле, необходимо определить как [8]
центрах в КП, помещенной в продольное магнитное поле, необходимо определить как [8]
 (2.1.31)
(2.1.31)
или в боровских единицах
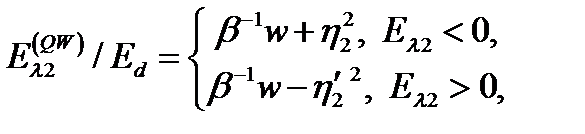 (2.1.32)
(2.1.32)
здесь 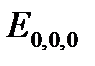 вычисляется по формуле (2.1.4).
вычисляется по формуле (2.1.4).
В случае, когда 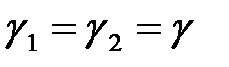 и
и 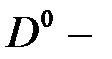 центры расположены в плоскости перпендикулярной оси КП
центры расположены в плоскости перпендикулярной оси КП  уравнения (2.1.23) и (2.1.24) сохранят свой вид, а коэффициенты
уравнения (2.1.23) и (2.1.24) сохранят свой вид, а коэффициенты 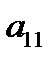 и
и 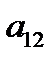 примут вид:
примут вид:
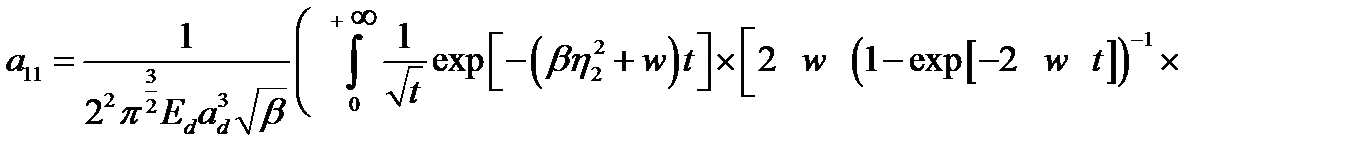
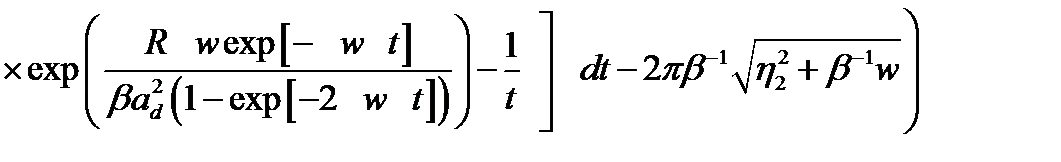 , (2.1.33)
, (2.1.33)
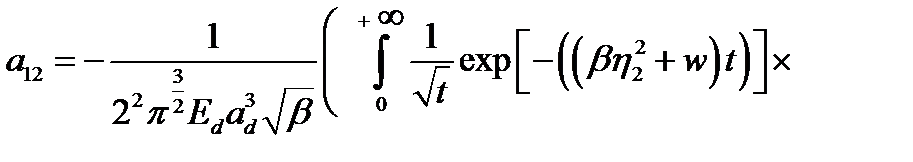

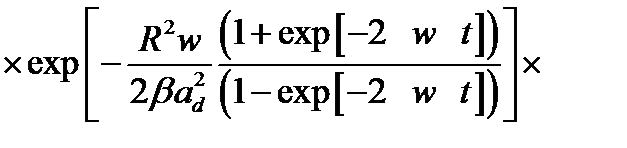
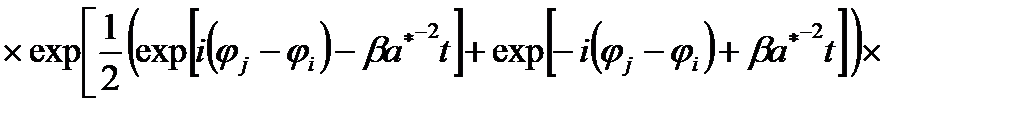
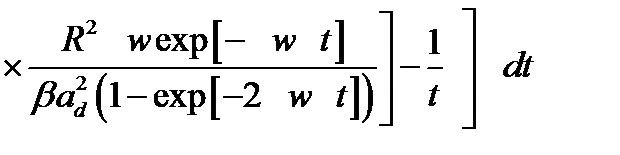 (2.1.34)
(2.1.34)
Соотношения (2.1.33) и (2.1.34) позволяют численно исследовать зависимость  и
и  термов от пространственной конфигурации
термов от пространственной конфигурации 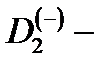 центра. Компьютерное исследование поведения термов молекулярного иона
центра. Компьютерное исследование поведения термов молекулярного иона 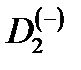 в КП при изменении параметров КП, величины внешнего магнитного поля, и пространственной конфигурации
в КП при изменении параметров КП, величины внешнего магнитного поля, и пространственной конфигурации 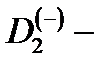 центра будет проведено в разделе 2.3.
центра будет проведено в разделе 2.3.
2.3 Сечение фотоионизации 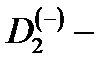 центра в квантовой проволоке
центра в квантовой проволоке
Рассмотрят процесс фотоионизации 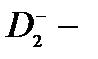 центра связанный с оптическим переходом электрона из
центра связанный с оптическим переходом электрона из 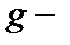 состояния в состояние квазидискретного спектра КН в продольном магнитном поле. Эффективный гамильтониан взаимодействия с полем световой волны
состояния в состояние квазидискретного спектра КН в продольном магнитном поле. Эффективный гамильтониан взаимодействия с полем световой волны 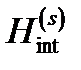 в случае продольной по отношению к направлению магнитного поля поляризации
в случае продольной по отношению к направлению магнитного поля поляризации  , дается выражением
, дается выражением
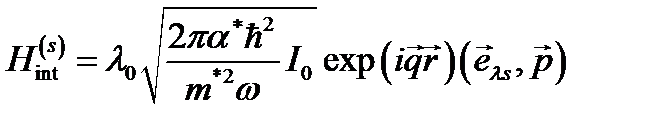 , (2.3.1)
, (2.3.1)
где  – коэффициент локального поля;
– коэффициент локального поля; 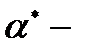 постоянная тонкой структуры с учетом диэлектрической проницаемости
постоянная тонкой структуры с учетом диэлектрической проницаемости  ;
; 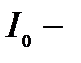 интенсивность света;
интенсивность света;  его частота;
его частота; 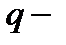 величина волнового вектора;
величина волнового вектора;  оператор импульса электрона.
оператор импульса электрона.
Согласно (2.1.9), волновую функцию электрона локализованного на  центре можно представить в виде
центре можно представить в виде
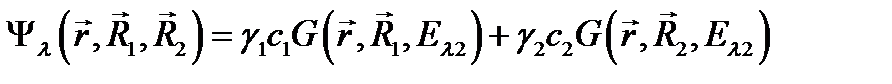 , (2.3.2)
, (2.3.2)
где одноэлектронные функции Грина 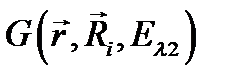 определяются формулой (2.1.20). В случае, когда
определяются формулой (2.1.20). В случае, когда 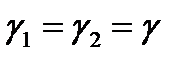 из (3.1.2) получим
из (3.1.2) получим
 , (2.3.3)
, (2.3.3)
здесь 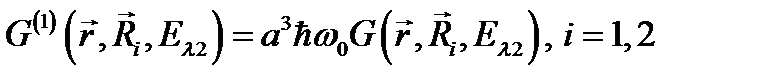 ; знак «+» в (2.3.3) соответствует
; знак «+» в (2.3.3) соответствует 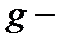 терму, а знак «–» –
терму, а знак «–» – 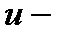 терму
терму 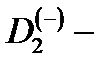 центра;
центра; 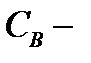 нормировочный множитель.
нормировочный множитель.
Проводили вычисление  для случая симметричного состояния, когда
для случая симметричного состояния, когда  :
:
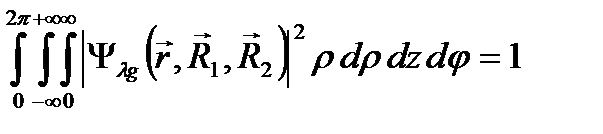 (2.3.4)
(2.3.4)
Согласно определению одноэлектронной функции Грина, имеем
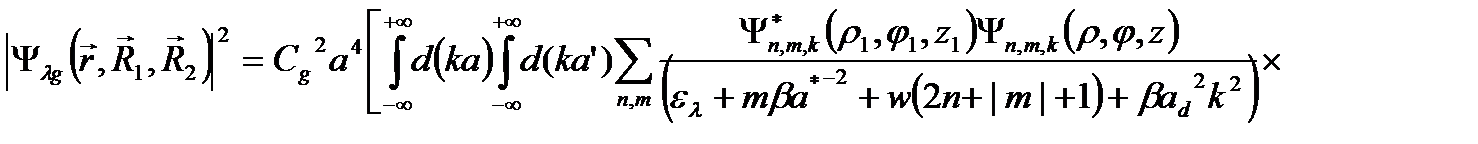
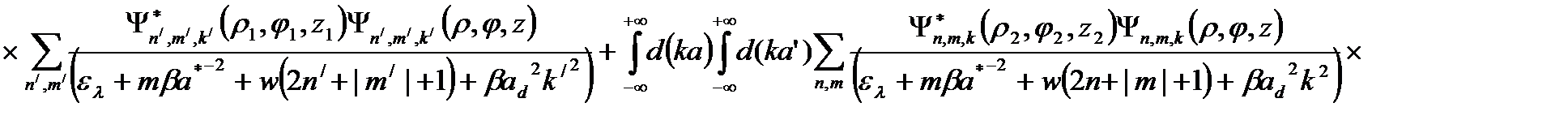

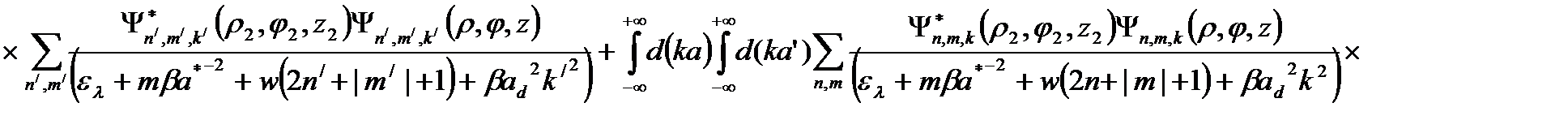
 , (2.3.5)
, (2.3.5)
где 
В результате необходимо вычислить интегралы вида:
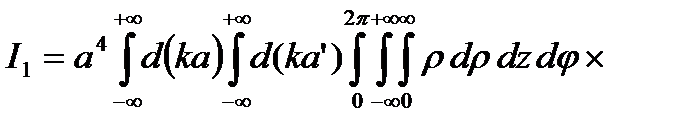
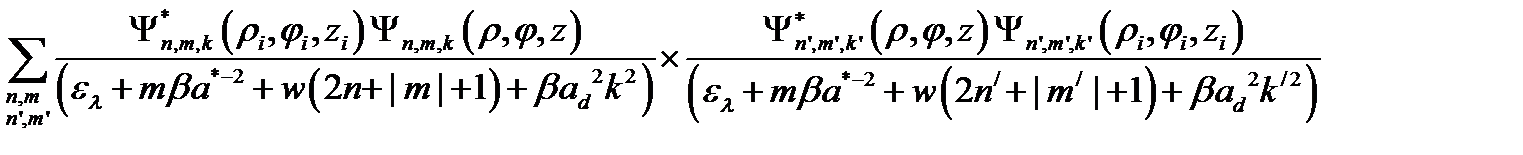 ,
,
(2.3.6)
где 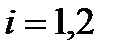
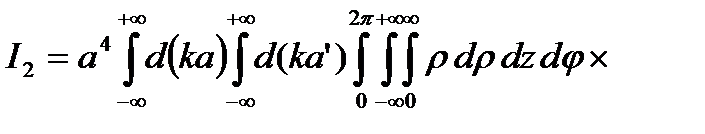
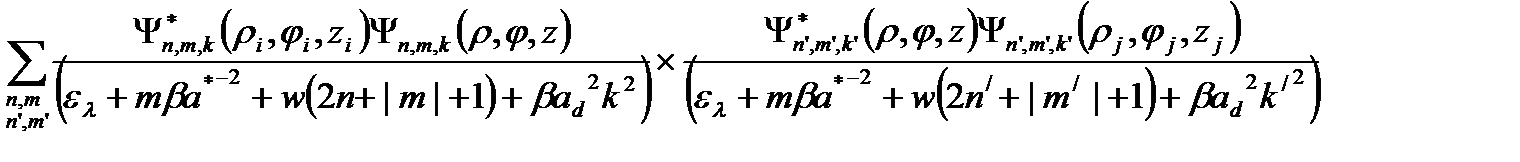 ,
,
(2.3.7)
где 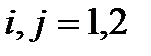
Так как одно частичные волновые функции образуют систему ортогональных функций, то в (2.3.6)
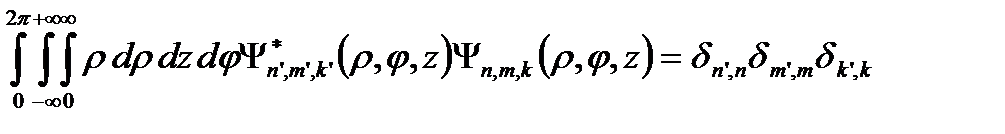 , (2.3.8)
, (2.3.8)
где 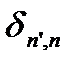 - символ Кронекера
- символ Кронекера
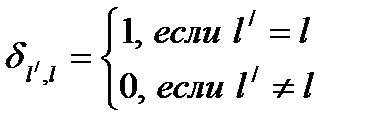 (2.3.9)
(2.3.9)
С учетом (2.3.8) получаем
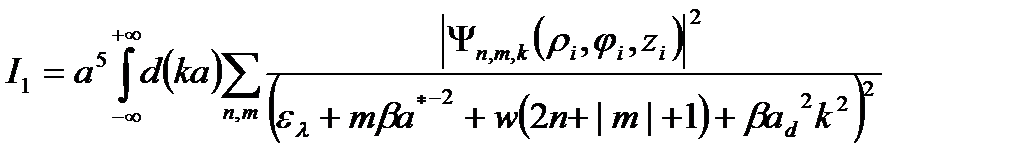 , (2.3.10)
, (2.3.10)
Учитывая, что
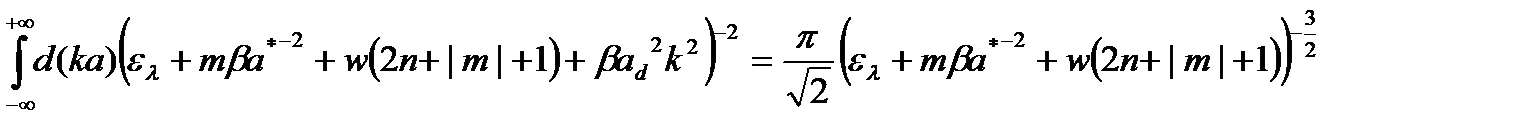 , (2.3.11)
, (2.3.11)
будем иметь
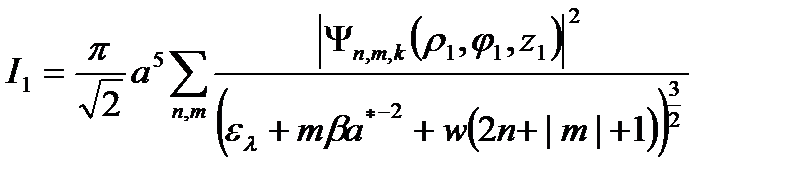 (2.3.12)
(2.3.12)
Тогда для безразмерной функции Грина получим следующее выражение:
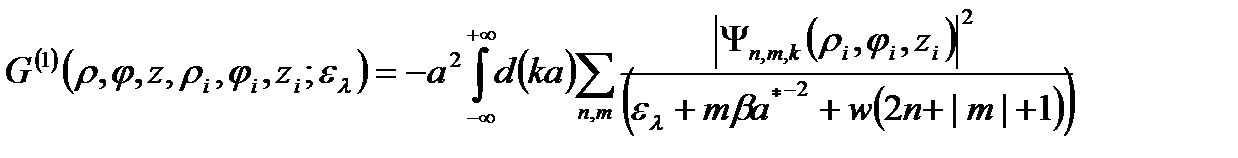 (2.3.13)
(2.3.13)
Вычисление производной приводит к следующему результату:
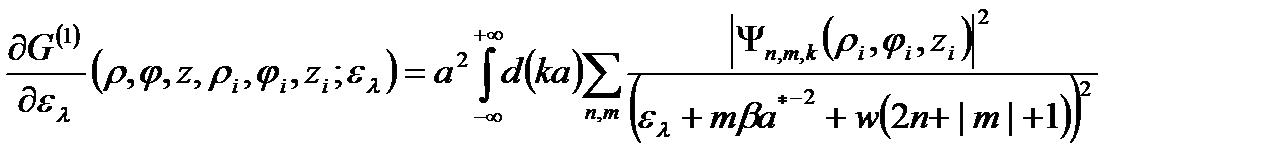 (2.3.14)
(2.3.14)
или с учетом (2.3.11)
 (2.3.15)
(2.3.15)
Подставляя (2.3.15) в (2.3.12) получим
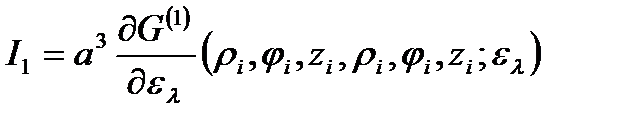 (2.3.16)
(2.3.16)
или в боровских единицах
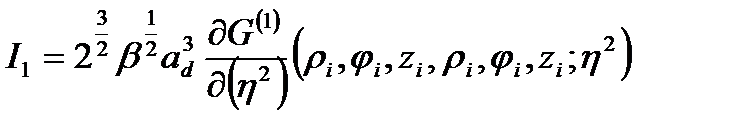 (2.3.17)
(2.3.17)
Рассмотрели случай, когда 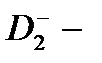 центр расположен на оси КП, т.е.
центр расположен на оси КП, т.е.
 (2.3.18)
(2.3.18)
С учетом (2.3.3) для производной  получили
получили
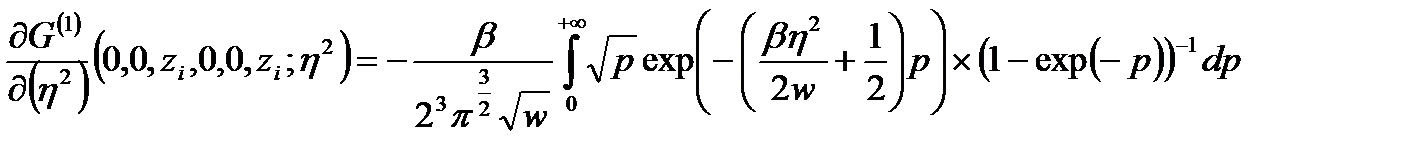 (2.3.19)
(2.3.19)
Учитывая, что [17]
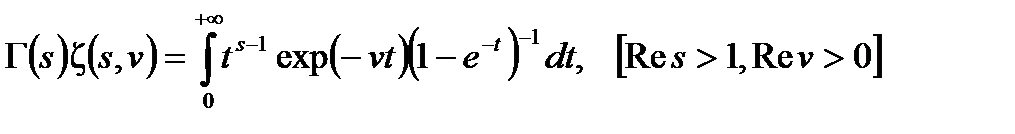 , (2.3.20)
, (2.3.20)
где 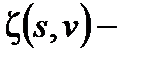 обобщенная дзета-функция, получаем для
обобщенная дзета-функция, получаем для 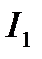 получим
получим
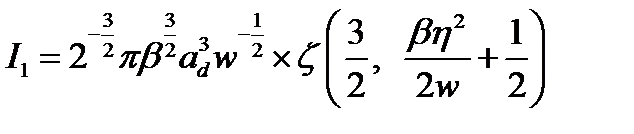 (2.3.21)
(2.3.21)
Вычисление интеграла 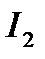 проводится в соответствии с описанной выше процедурой для
проводится в соответствии с описанной выше процедурой для  , применяя которую для
, применяя которую для  получили
получили
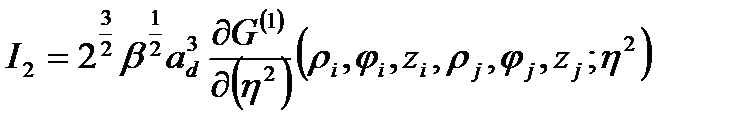 (2.3.22)
(2.3.22)
В случае расположения примесных атомов на оси КП получили:
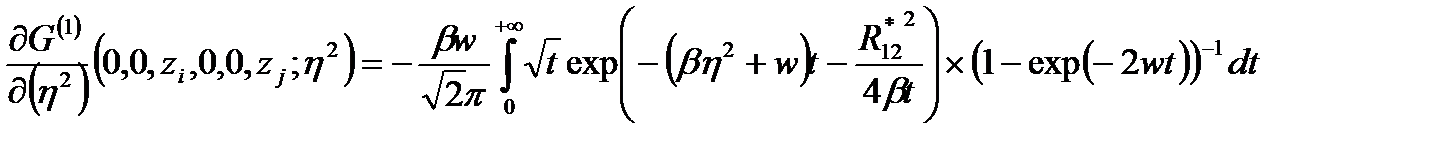 (2.3.23)
(2.3.23)
Вычисление интеграла в (3.1.23), используя известные соотношения [16], дает следующий результат
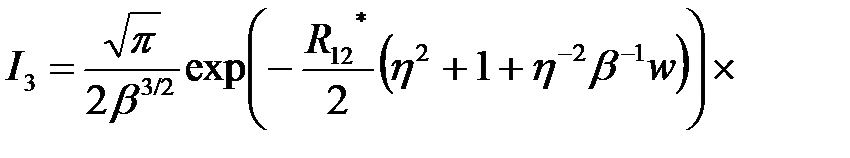
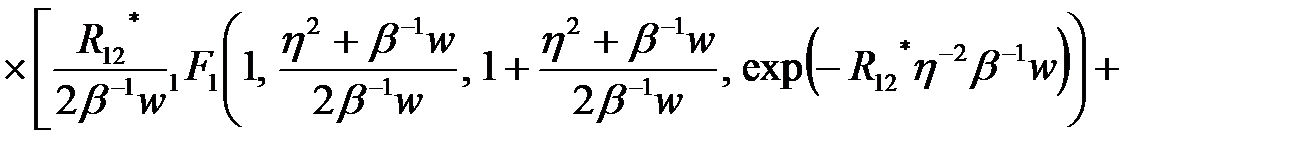
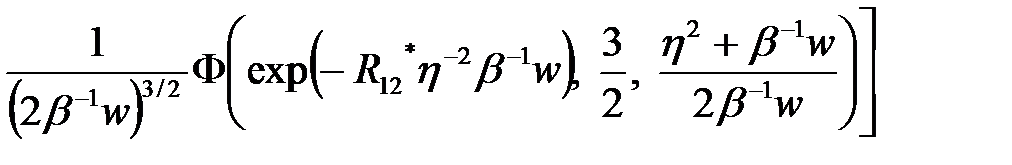 (2.3.24)
(2.3.24)
Таким образом, для нормировочного множителя 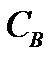 волновой функции электрона локализованного на
волновой функции электрона локализованного на 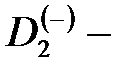 центре получили:
центре получили:
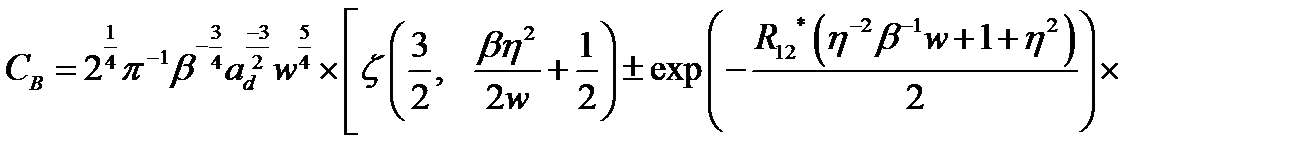
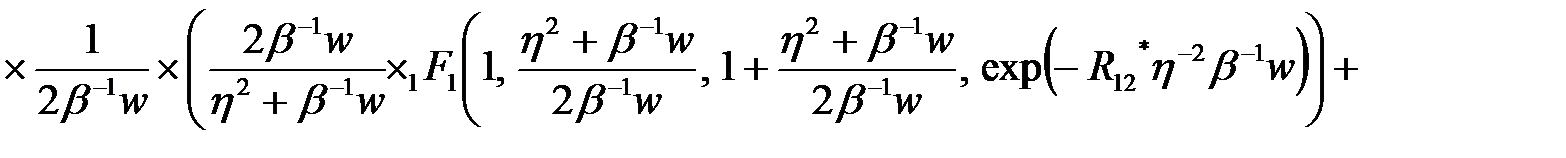
 (2.3.25)
(2.3.25)
Матричный элемент  , определяющий величину силы осциллятора дипольных оптических переходов электрона из состояния
, определяющий величину силы осциллятора дипольных оптических переходов электрона из состояния 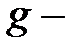 терма
терма 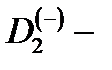 центра в состояния
центра в состояния 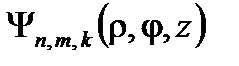 квазидискретного спектра КП, находящейся в магнитном поле, в случае продольной поляризации
квазидискретного спектра КП, находящейся в магнитном поле, в случае продольной поляризации 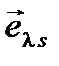 света запишется как
света запишется как
 =
=  (2.3.26)
(2.3.26)
Учитывая выражения для волновой функции начального  и конечного состояния
и конечного состояния 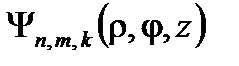
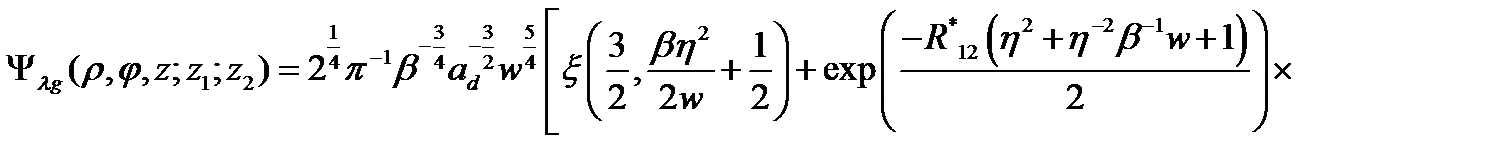
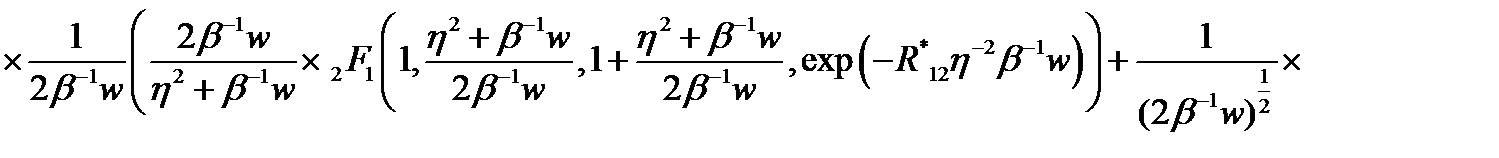


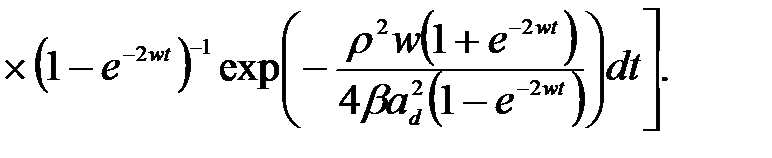 (2.3.27)
(2.3.27)

(2.3.28)
а также (2.3.1), для  получили
получили
 =
= 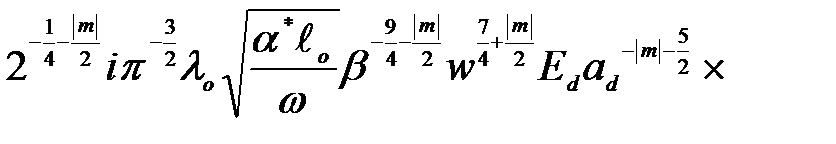
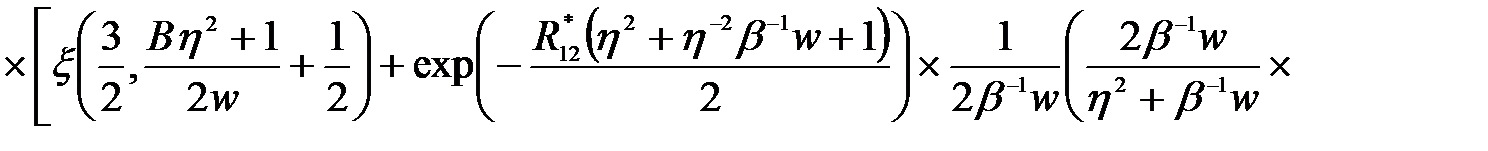
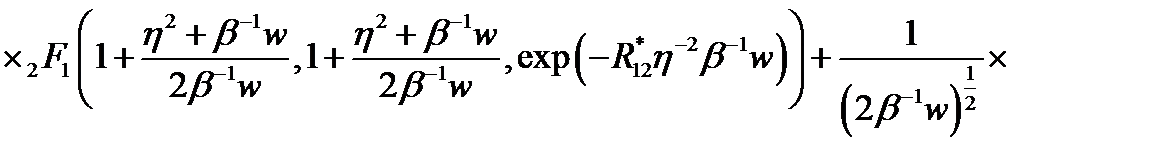
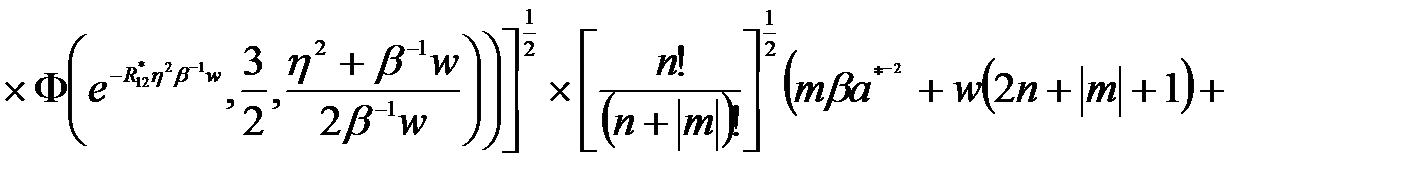

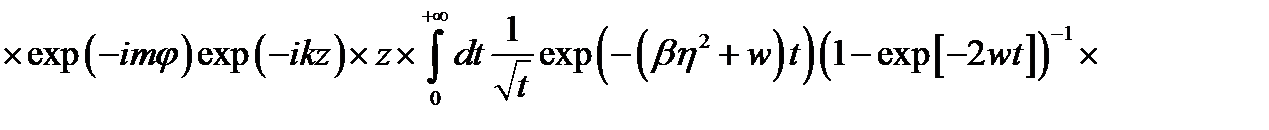
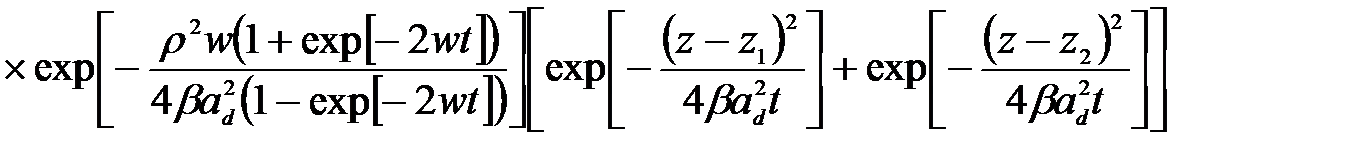 (2.3.29)
(2.3.29)
При вычислении матричного элемента появляются интегралы вида:
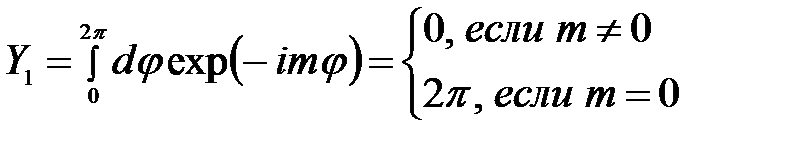
(2.3.30)

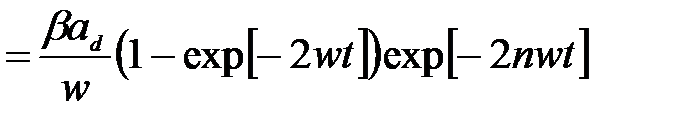 (2.3.31)
(2.3.31)
Из (2.3.30) видно, что правила отбора таковы, что оптические переходы из состояния 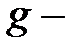 терма возможны только в состояния КП со значением магнитного квантового числа
терма возможны только в состояния КП со значением магнитного квантового числа 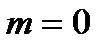 . Интегрирование по переменной
. Интегрирование по переменной  в (2.3.29) сводится к вычислению интеграла вида
в (2.3.29) сводится к вычислению интеграла вида
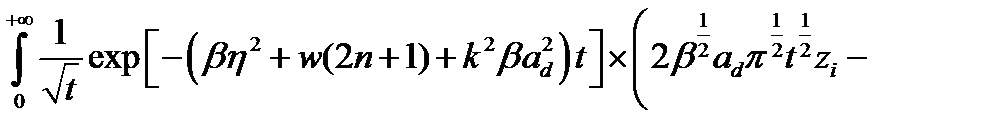
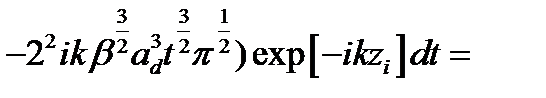
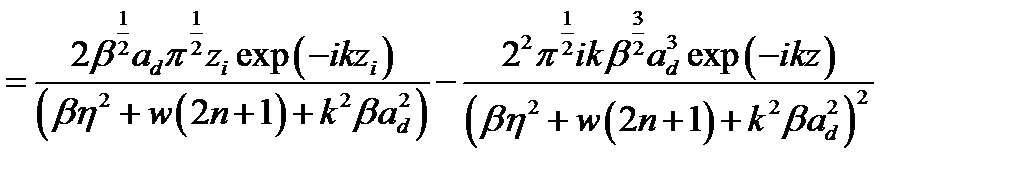 , (2.3.32)
, (2.3.32)
Полагая  , (в этом случае
, (в этом случае  – расстояние между
– расстояние между 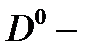 центрами), а в (2.3.29) получено
центрами), а в (2.3.29) получено
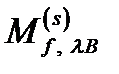 =
= 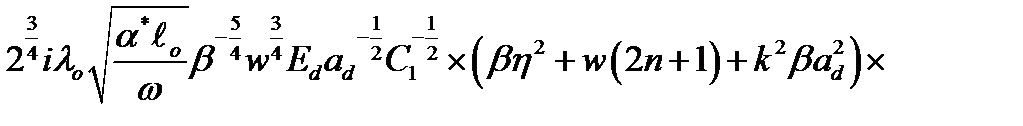

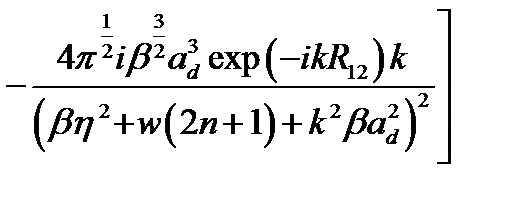 , (2.3.33)
, (2.3.33)
где 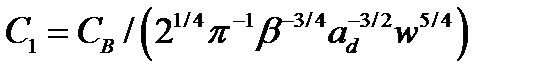 .
.
Выделяя действительную и мнимую части  получили
получили
 =
= 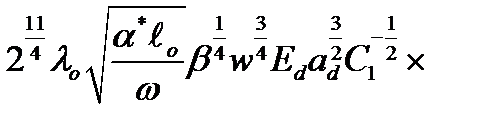
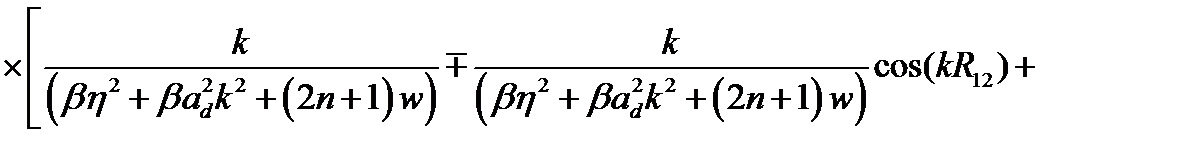
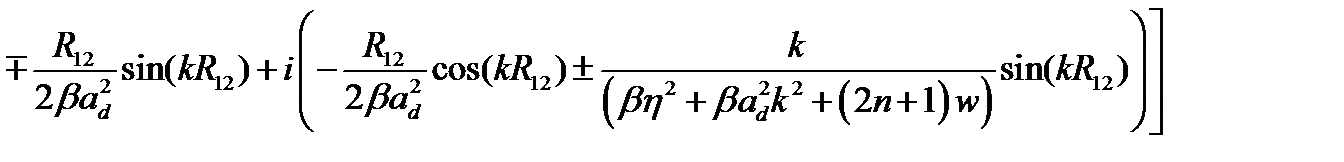 (2.3.34)
(2.3.34)
С учетом (2.3.34) квадрат модуля матричного элемента  запишется как
запишется как
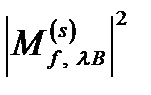 =
= 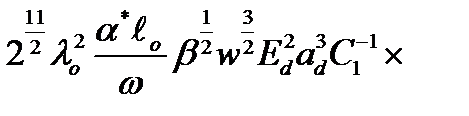
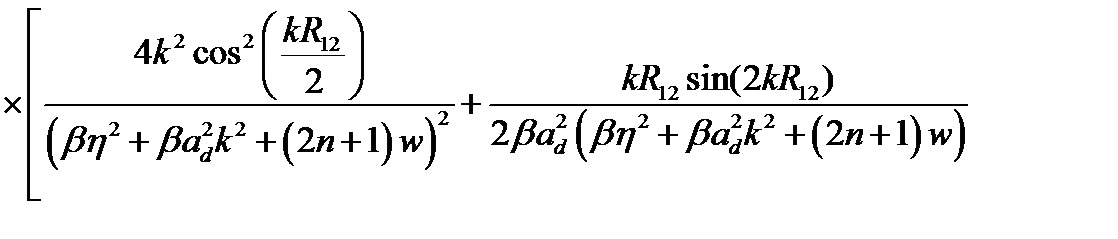
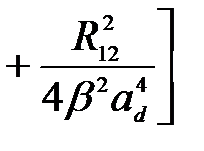 (2.3.35)
(2.3.35)
Сечение фотоионизации 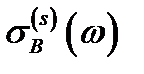
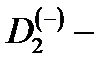 центра в случае поглощения света продольной, по отношению к оси КП поляризации
центра в случае поглощения света продольной, по отношению к оси КП поляризации  определяется формулой
определяется формулой
 (3.1.36)
(3.1.36)
Далее, используя стандартную процедуру расчета, описанную в главе 1, для 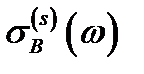 получили
получили
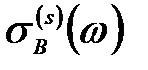
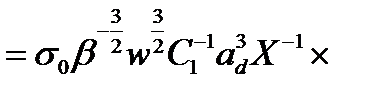
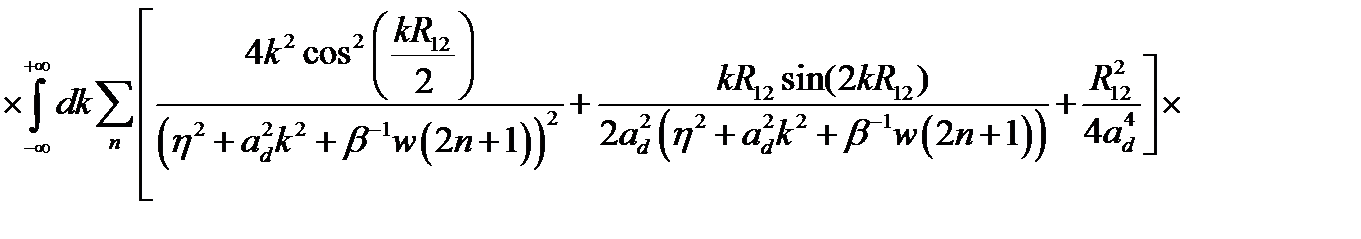
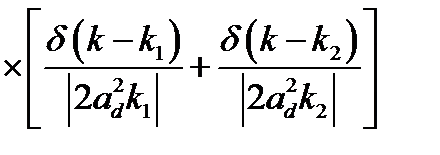 , (2.3.37)
, (2.3.37)
где 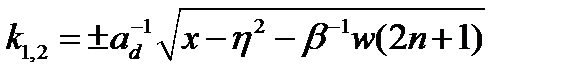 – корни аргумента
– корни аргумента 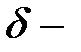 функции,
функции, 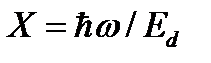 .
.
После интегрирования в (2.3.37) для сечения фотоионизации при оптических переходах электрона из состояния  терма
терма  центра в состояния
центра в состояния 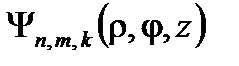 квазидискретного спектра КП получили [A5]:
квазидискретного спектра КП получили [A5]:
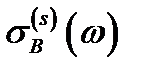
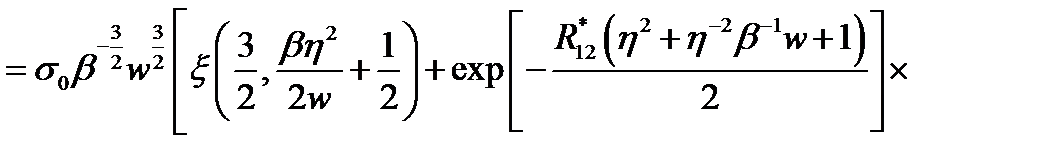

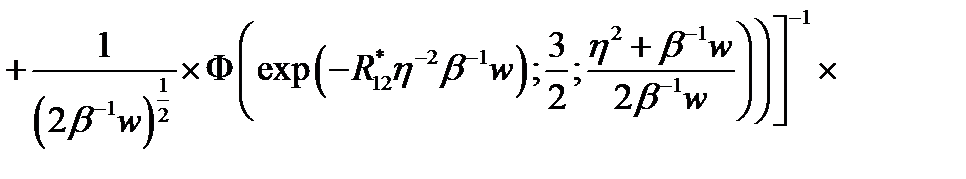
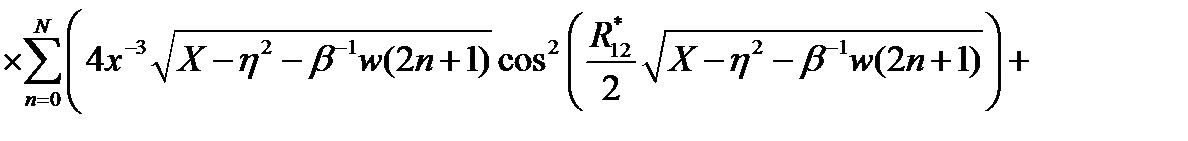
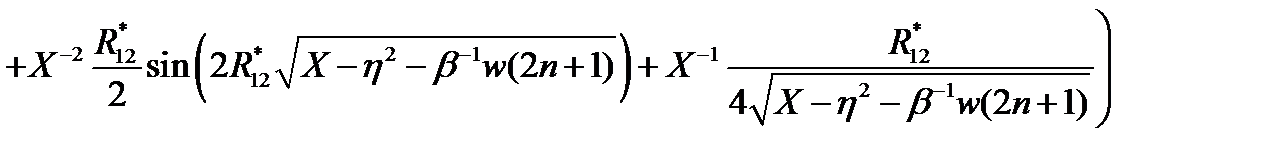 , (2.3.38)
, (2.3.38)
где  ,
, 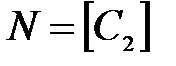 ,
, 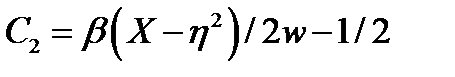
На рис.23 представлена спектральная зависимость 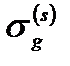 , рассчитанная по формуле (2.3.38) для КП на основе InSb. Видно, что спектр магнито поглощения света продольной поляризации содержит резонансные пики с ярко выраженными осцилляциями интерференционной природы. Резонансные пики появляются с периодом, определяемым гибридной частотой
, рассчитанная по формуле (2.3.38) для КП на основе InSb. Видно, что спектр магнито поглощения света продольной поляризации содержит резонансные пики с ярко выраженными осцилляциями интерференционной природы. Резонансные пики появляются с периодом, определяемым гибридной частотой 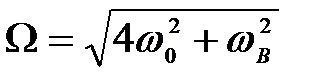 и соответствуют оптическим переходам электрона из
и соответствуют оптическим переходам электрона из 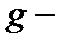 состояния
состояния 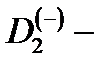 центра в состояния квазидискретного спектра КП с
центра в состояния квазидискретного спектра КП с 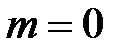 . В магнитном поле край поглощения сдвигается в коротковолновую область спектра (ср. кривые 1 и 2). В случае, когда
. В магнитном поле край поглощения сдвигается в коротковолновую область спектра (ср. кривые 1 и 2). В случае, когда 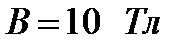 этот сдвиг, как нетрудно видеть из рис.23, составляет почти
этот сдвиг, как нетрудно видеть из рис.23, составляет почти 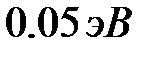 и происходит по закону
и происходит по закону
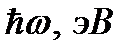
|
| 2 |
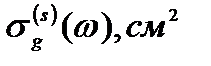
|
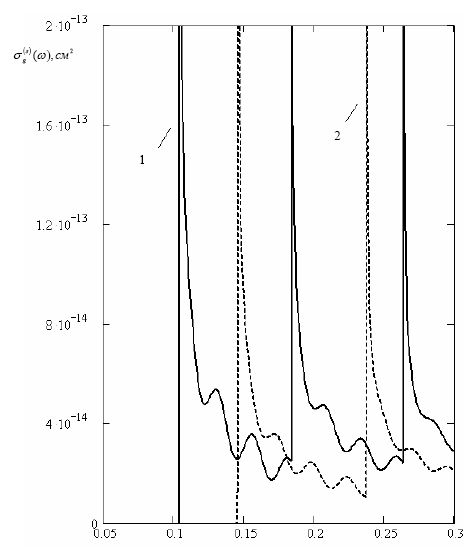
Рис.23 Спектральная зависимость сечения фотоионизации 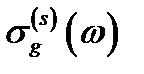
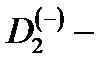 центра для случая продольной поляризации света при
центра для случая продольной поляризации света при 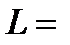 65 нм,
65 нм, 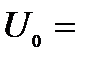 0,1 эВ,
0,1 эВ, 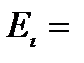 0,001 эВ,
0,001 эВ,  =16 нм: 1 –
=16 нм: 1 –  0 Тл, 2 –
0 Тл, 2 – 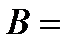 10 Тл
10 Тл
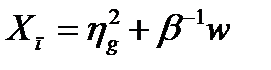 , где
, где 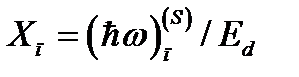 . При этом амплитуда осцилляций заметно уменьшается. Зависимость края полосы примесного поглощения света продольной по отношению к оси КП поляризации от величины магнитного поля приведена на рис.24.
. При этом амплитуда осцилляций заметно уменьшается. Зависимость края полосы примесного поглощения света продольной по отношению к оси КП поляризации от величины магнитного поля приведена на рис.24.
Выяснили природу осцилляций в спектрах магнитооптического поглощения КП с 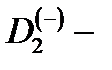 центром. С этой целью рассмотрят формально амплитуду оптического перехода электрона из
центром. С этой целью рассмотрят формально амплитуду оптического перехода электрона из 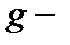 состояния в гибридно-квантованные состояния КП в дипольном приближении
состояния в гибридно-квантованные состояния КП в дипольном приближении 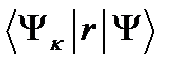 , где
, где 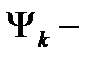 волновая функция конечного состояния, а
волновая функция конечного состояния, а 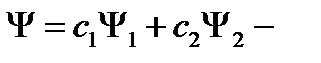 волновая функция начального состояния электрона, локализованного на
волновая функция начального состояния электрона, локализованного на 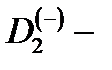 центре. Для
центре. Для 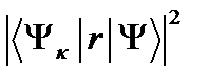 получено, учитывая, что для
получено, учитывая, что для  терма
терма 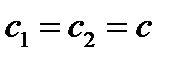 :
:

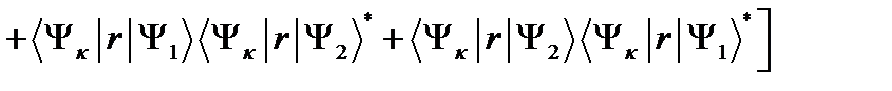 (2.3.39)
(2.3.39)
Можно видеть, что результирующая амплитуда перехода не равна сумме амплитуд оптических переходов из состояния каждого 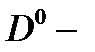 центра в отдельности, т.е. в соотношении (2.3.39) содержатся два дополнительных слагаемых, обусловленные интерференцией амплитуд. Таким образом, осцилляции в спектрах магнитооптического поглощения являются следствием интерференции амплитуд двух возможных оптических переходов электрона в конечное состояние КП. На рис.25 приведены результаты численного исследования зависимости периода осцилляций заполняющих расстояние между резонансными пиками на спектральной кривой для случая продольной поляризации света от расстояния между
центра в отдельности, т.е. в соотношении (2.3.39) содержатся два дополнительных слагаемых, обусловленные интерференцией амплитуд. Таким образом, осцилляции в спектрах магнитооптического поглощения являются следствием интерференции амплитуд двух возможных оптических переходов электрона в конечное состояние КП. На рис.25 приведены результаты численного исследования зависимости периода осцилляций заполняющих расстояние между резонансными пиками на спектральной кривой для случая продольной поляризации света от расстояния между 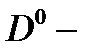 центрами и величины магнитного поля. Из рис.25 видно, что период осцилляций линейно растет с уменьшением расстояния между
центрами и величины магнитного поля. Из рис.25 видно, что период осцилляций линейно растет с уменьшением расстояния между 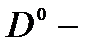 центрами
центрами 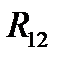 и слабо зависит от величины магнитного поля.
и слабо зависит от величины магнитного поля.
Рис. 24 Зависимость порогового значения энергии фотона 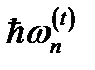 для случая примесного поглощения света продольной поляризации в КП на основе InSb (
для случая примесного поглощения света продольной поляризации в КП на основе InSb (  , L=65 нм, U0=0.2 эВ) от величины магнитной индукции B:
, L=65 нм, U0=0.2 эВ) от величины магнитной индукции B:
1 – 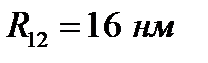 ; 2. –
; 2. – 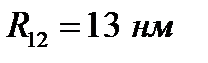 ; 3. –
; 3. – 
Рис.25 Зависимость периода осцилляций между спектральными резонансными пиками от расстояния между  центрами при
центрами при  ; L=65 нм; U0=0.2 эВ для различных значений магнитного поля:
; L=65 нм; U0=0.2 эВ для различных значений магнитного поля:
1 – 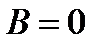 Тл; 2 –
Тл; 2 –  Тл; 3 –
Тл; 3 –  Тл
Тл
Рассматривается поглощение света системой «КН – 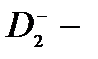 центр» в случае, когда
центр» в случае, когда 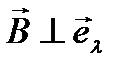 (
(  единичный вектор поляризации света). Эффективный гамильтониан взаимодействия с полем световой волны
единичный вектор поляризации света). Эффективный гамильтониан взаимодействия с полем световой волны 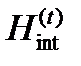 в цилиндрической системе координат запишется в виде:
в цилиндрической системе координат запишется в виде:
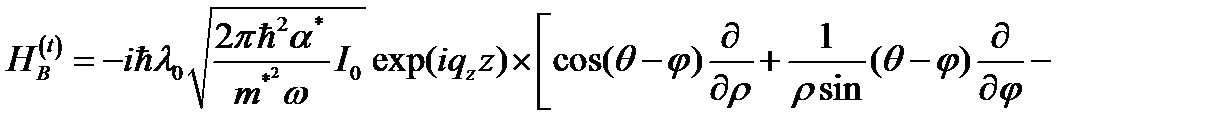
 , (2.3.40)
, (2.3.40)
где  – полярный угол единичного вектора поперечной поляризации
– полярный угол единичного вектора поперечной поляризации  в цилиндрической системе координат.
в цилиндрической системе координат.
В дипольном приближении матричный элемент 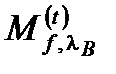 рассматриваемого оптического перехода электрона из состояния
рассматриваемого оптического перехода электрона из состояния  терма
терма  центра в состояния
центра в состояния 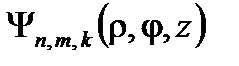 квазидискретного спектра КП запишется в виде
квазидискретного спектра КП запишется в виде
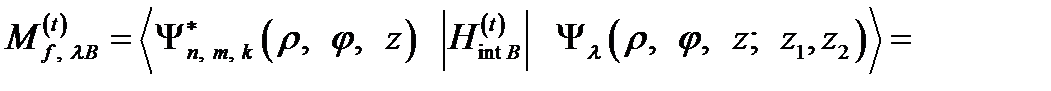
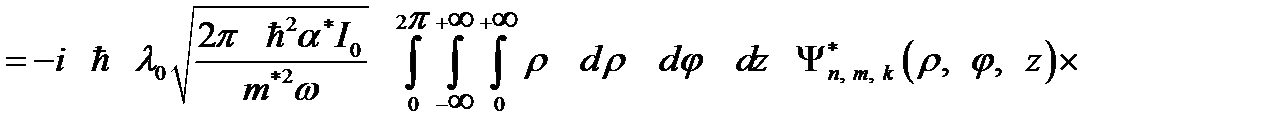
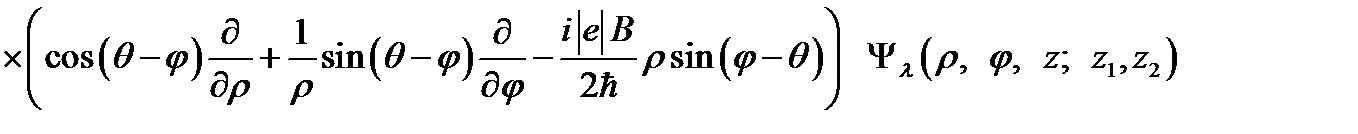 (2.3.41)
(2.3.41)
С учетом одноэлектронных состояний в продольном магнитном поле (2.3.3) и волновой функции (2.3.27) связанного состояния в КП, матричный элемент 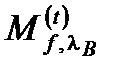 можно представить как
можно представить как
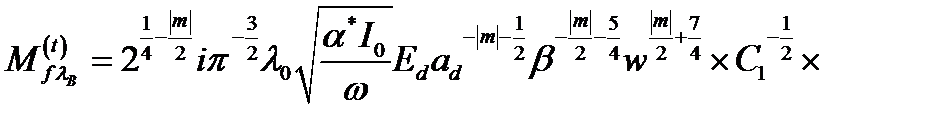
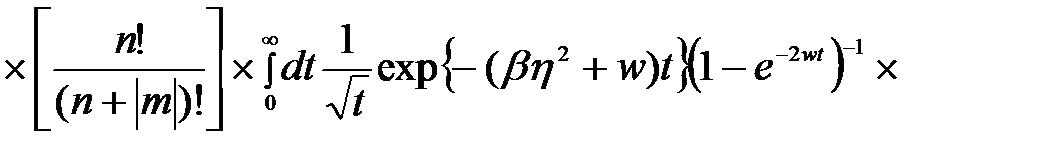
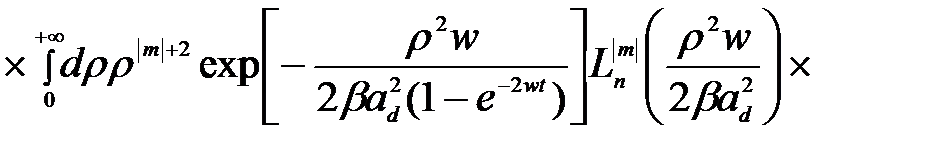

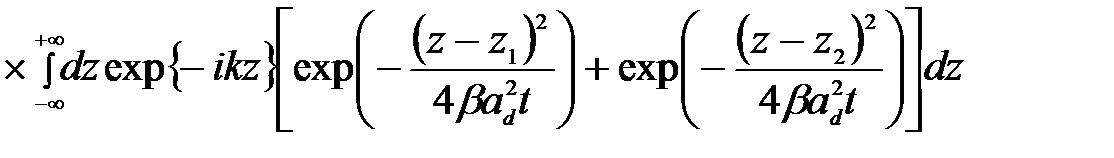 (2.3.42)
(2.3.42)
При расчете матричного элемента в (2.3.42) появляются интегралы вида

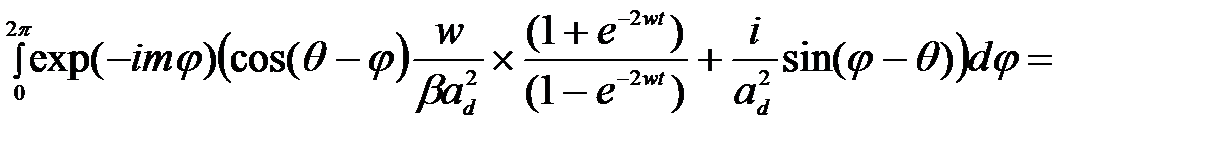
 , (2.3.43)
, (2.3.43)
здесь 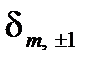 – символ Кронекера
– символ Кронекера
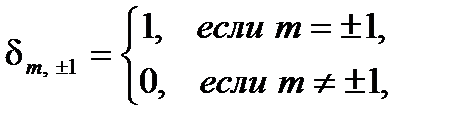 (2.3.44)
(2.3.44)
знак «–» в показателе степени 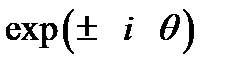 соответствует значению
соответствует значению 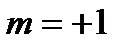 , а знак «+» —
, а знак «+» —  . Из (2.3.43) и (2.3.44) видно, что оптические переходы с
. Из (2.3.43) и (2.3.44) видно, что оптические переходы с 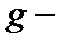 терма могут происходить только в состояния КП со значениями магнитного квантового числа
терма могут происходить только в состояния КП со значениями магнитного квантового числа 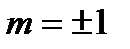 . Дальнейшие вычисления в (2.3.42) сводятся к интегралу вида:
. Дальнейшие вычисления в (2.3.42) сводятся к интегралу вида:

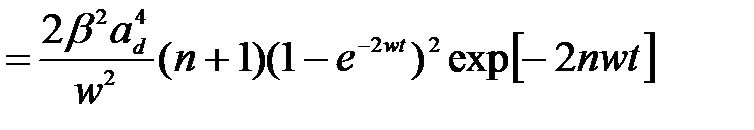 (2.3.45)
(2.3.45)
Интегрирование по координате 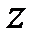 дает
дает

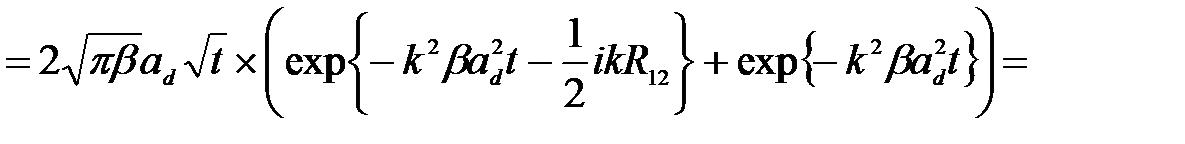
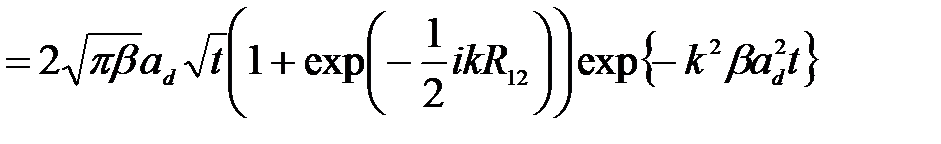 (2.3.46)
(2.3.46)
Учитывая (2.3.43), (2.3.45), (2.3.42) и (2.3.46), для матричного элемента 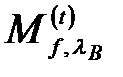 окончательно получено
окончательно получено
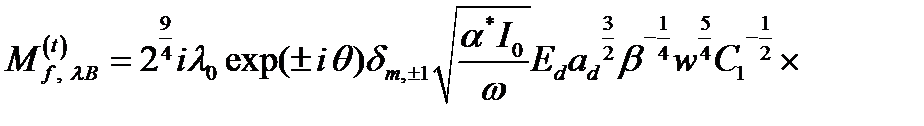
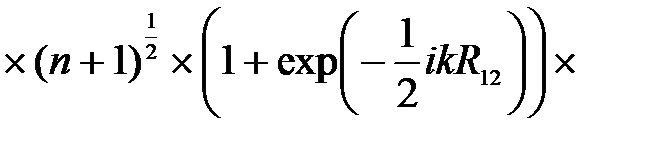
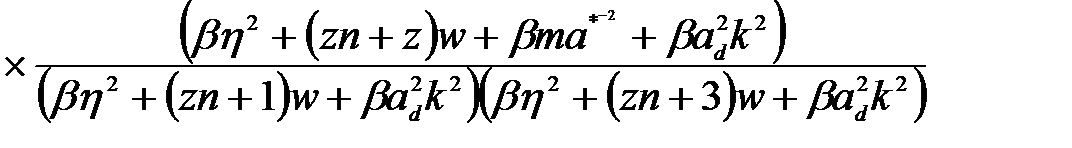 (2.3.47)
(2.3.47)
Квадрат модуля матричного элемента запишется как

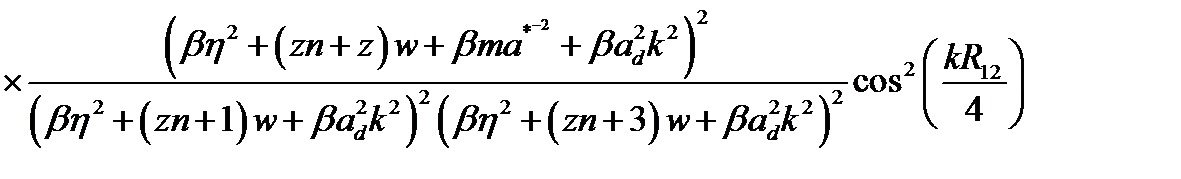 (2.3.48)
(2.3.48)
Сечение фотоионизации 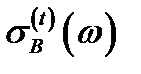 с учетом правил отбора (2.3.43) были представлены в виде
с учетом правил отбора (2.3.43) были представлены в виде
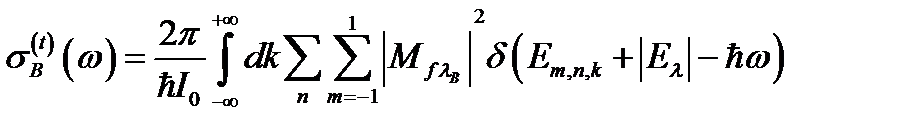 (2.3.49)
(2.3.49)
Интегрирование по переменной 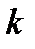 в (2.3.49) предполагает нахождение корней аргумента d-функции Дирака
в (2.3.49) предполагает нахождение корней аргумента d-функции Дирака
 (2.3.50)
(2.3.50)
или
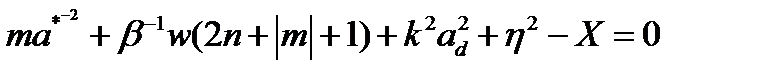 (2.3.51)
(2.3.51)
Корни уравнения (2.3.51) имеют вид
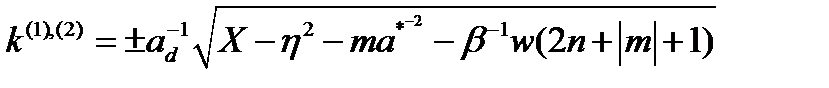 (3.1.52)
(3.1.52)
С учетом (2.3.52) для 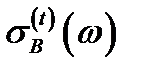 получено [A5]
получено [A5]
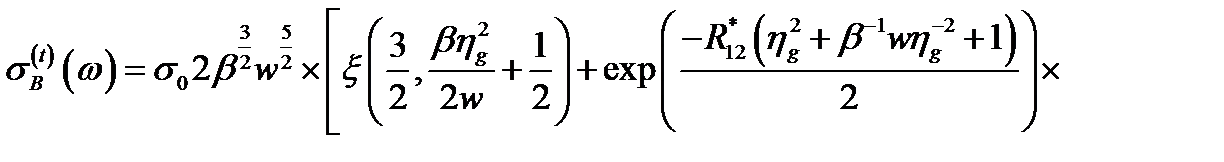
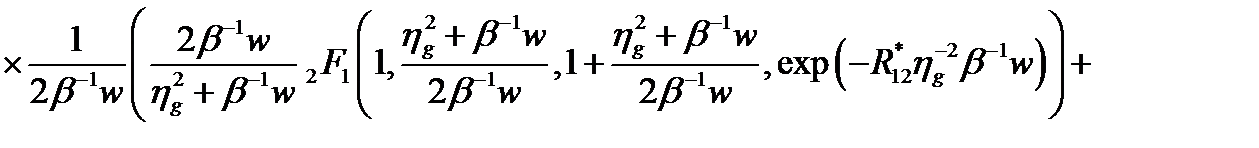
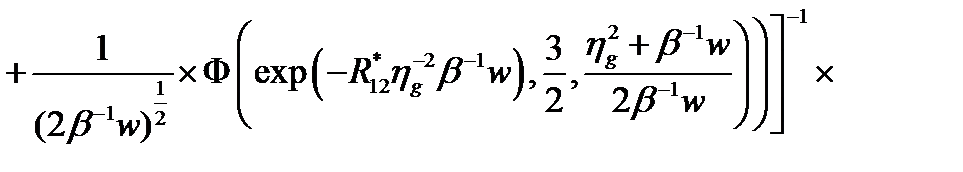
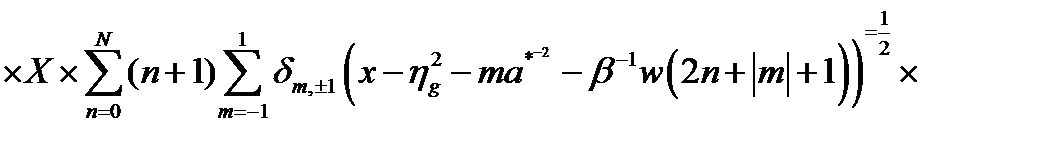

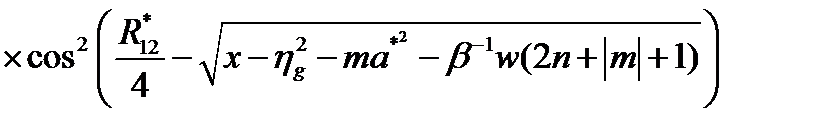 , (2.3.53)
, (2.3.53)
где 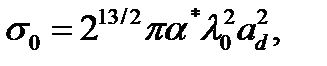
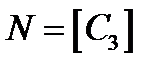 целая часть числа
целая часть числа 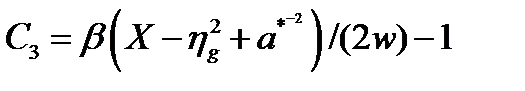 .
.
Пороговое значение энергии фотона для случая поперечной поляризации света 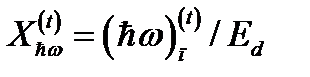 определиться как
определиться как 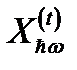
 .
.
На рис.26 приведена спектральная зависимость сечения фотоионизации  центра
центра 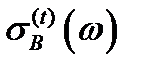 , рассчитанная по формуле (2.3.53) в случае КП на основе InSb. Можно видеть, что магнитном поле резонансные пики
, рассчитанная по формуле (2.3.53) в случае КП на основе InSb. Можно видеть, что магнитном поле резонансные пики 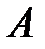 и
и 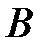 (кривая 1) расщепляются в дублеты
(кривая 1) расщепляются в дублеты 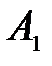 и
и 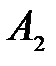 ,
, 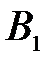 и
и  (кривая 2) соответственно. Промежутки между пиками в дублете Зеемана «заполнены» осцилляциями интерференционной природы. Расстояние между резонансными пиками, составляющими дублет, равно
(кривая 2) соответственно. Промежутки между пиками в дублете Зеемана «заполнены» осцилляциями интерференционной природы. Расстояние между резонансными пиками, составляющими дублет, равно 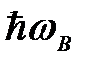 , т.е. определяется циклотронной частотой. Дублеты расположены периодично на кривой поглощения с периодом равным
, т.е. определяется циклотронной частотой. Дублеты расположены периодично на кривой поглощения с периодом равным 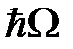 . Период осцилляций в дублете и между дублетами, как показал численный анализ, экспоненциально возрастает с уменьшением расстояния между
. Период осцилляций в дублете и между дублетами, как показал численный анализ, экспоненциально возрастает с уменьшением расстояния между  центрами и незначительно меняется с ростом магнитного поля (см. рис.27)
центрами и незначительно меняется с ростом магнитного поля (см. рис.27)
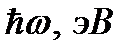
|
| 2 |
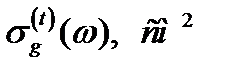
|

Рис.26 Спектральная зависимость сечения фотоионизации 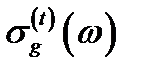
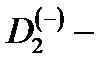 центра в КП на основе InSb для случая поперечной поляризации света при
центра в КП на основе InSb для случая поперечной поляризации света при 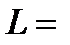 65 нм,
65 нм, 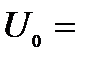 0,1 эВ,
0,1 эВ, 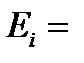 0,001 эВ,
0,001 эВ,  =16 нм:
=16 нм:
1 – 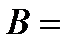 0 Тл, 2 –
0 Тл, 2 – 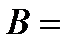 10 Тл
10 Тл
Приведенные в данном разделе результаты показывают, что приложенное вдоль оси КП магнитное поле играет роль варьируемого параметра, посредством которого можно достаточно эффективно управлять как величиной энергии связи 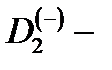 центров, так и их магнитооптическими свойствами. Это важно для создания фоточувствительных структур с управляемыми параметрами.
центров, так и их магнитооптическими свойствами. Это важно для создания фоточувствительных структур с управляемыми параметрами.
В случае структуры, представляющей собой набор туннельно-несвязанных КП, коэффициент примесного магнитопоглощения света 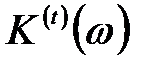 поперечной поляризации можно получить из (2.3.53) путем усреднения по всем возможным значениям расстояния
поперечной поляризации можно получить из (2.3.53) путем усреднения по всем возможным значениям расстояния 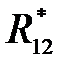 между
между 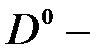 центрами с учетом экспоненциально малого вклада больших
центрами с учетом экспоненциально малого вклада больших  :
:
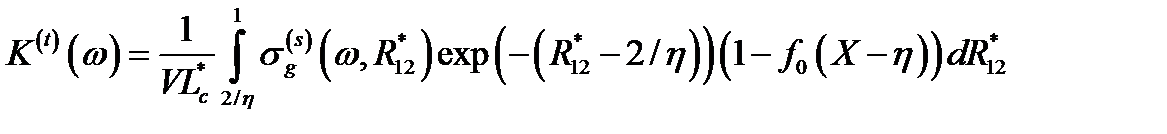 , (2.3.54)
, (2.3.54)
где 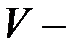 объем КП;
объем КП;  период структуры в единицах эффективного боровского радиуса;
период структуры в единицах эффективного боровского радиуса; 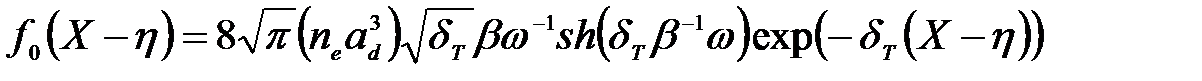 – квазиравновесная функция распределения электронов в КП [80];
– квазиравновесная функция распределения электронов в КП [80]; 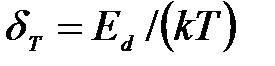 ;
; 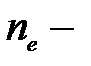 концентрация электронов.
концентрация электронов.
На рис.26 приведена спектральная зависимость коэффициента примесного магнитопоглощения света поперечной поляризации в относительных единицах 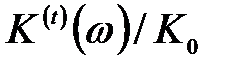 , где
, где 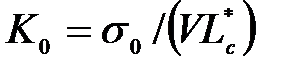 , для оптического перехода с максимальной силой осциллятора (
, для оптического перехода с максимальной силой осциллятора ( 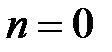 ) в случае КП на основе InSb. Из сравнения рис. 26 и 28 видно, что резонансные пики
) в случае КП на основе InSb. Из сравнения рис. 26 и 28 видно, что резонансные пики 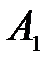 и
и 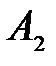 в дублете (рис. 26) размываются в полосы (рис.28), размываются также и осцилляции в дублете. Оценка величины
в дублете (рис. 26) размываются в полосы (рис.28), размываются также и осцилляции в дублете. Оценка величины  в дублете для КП на основе InSb при следующих численных значениях параметров (см. рис. 26):
в дублете для КП на основе InSb при следующих численных значениях параметров (см. рис. 26):  65 нм,
65 нм, 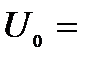 0,1 эВ,
0,1 эВ,  0,001 эВ,
0,001 эВ, 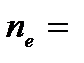 1,4*1016 см-3,
1,4*1016 см-3, 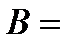 20 Тл,
20 Тл,  7 К,
7 К, 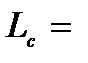 70 нм, дает
70 нм, дает 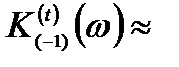 3,6*103 см-1 и
3,6*103 см-1 и 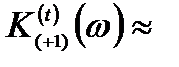 5,4*103 см-1 соответственно в максимумах кривых
5,4*103 см-1 соответственно в максимумах кривых 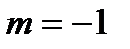 и
и 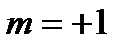 , что по порядку величины сравнимо с коэффициентом
, что по порядку величины сравнимо с коэффициентом
Рис.28 Спектральная зависимость коэффициента примесного поглощения света в КН на основе  с максимальной силой осциллятора (
с максимальной силой осциллятора ( 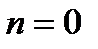 ) при
) при  65 нм,
65 нм, 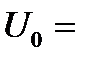 0,1 эВ,
0,1 эВ, 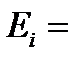 0,001 эВ,
0,001 эВ, 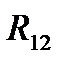 =16 нм:,
=16 нм:, 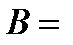 20 Тл,
20 Тл, 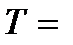 7 К
7 К
поглощения на прямых межзонных переходах в многоямной квантовой структуре в отсутствии квантующего магнитного поля [81].
Заключение
1. В рамках модели потенциала нулевого радиуса в приближении эффективной массы аналитически получены дисперсионные уравнения локализованного на  центре электрона, определяющие симметричное (
центре электрона, определяющие симметричное ( 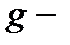 терм) и антисимметричное (
терм) и антисимметричное ( 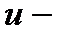 терм) состояния электрона соответственно в КП и МС при наличии продольного магнитного поля.
терм) состояния электрона соответственно в КП и МС при наличии продольного магнитного поля.
2. Показано, что магнитное поле приводит к значительному изменению положения термов и стабилизации 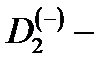 состояний в КП и МС.
состояний в КП и МС.
Установлено, что эффективная длина МС существенно влияет как на величину расщепления между термами, так и на размер области, где возможно существование 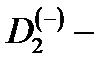 состояний.
состояний.
Исследовано влияние фактора пространственной конфигурации отрицательного молекулярного иона  в КП на
в КП на 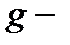 и
и 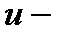 термы, а также на величину расщепления между термами.
термы, а также на величину расщепления между термами.
3. Показано, что для планарной конфигурации 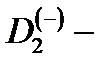 центра в КП и МС близость границ системы приводит к излому энергетических уровней, соответствующих вырожденным
центра в КП и МС близость границ системы приводит к излому энергетических уровней, соответствующих вырожденным 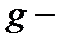 и
и 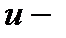 состояниям.
состояниям.
4. В дипольном приближении получены аналитические формулы сечений фотоионизации 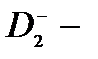 центров в квантовой проволоке для случая поперечной и продольной по отношению к направлению магнитного поля поляризации света.
центров в квантовой проволоке для случая поперечной и продольной по отношению к направлению магнитного поля поляризации света.
Показано, что спектр магнитопоглощения света продольной поляризации содержит резонансные пики с ярко выраженными осцилляциями. интерференционной природы. Установлено, что осцилляции в спектрах магнитооптического поглощения являются следствием интерференции амплитуд двух возможных оптических переходов электрона в конечное состояние КП.
5. Найдено, что период осцилляций линейно растет с уменьшением расстояния между 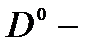 центрами и слабо зависит от величины магнитного поля. Резонансные пики обнаруживают периодичность, определяемую гибридной частотой.
центрами и слабо зависит от величины магнитного поля. Резонансные пики обнаруживают периодичность, определяемую гибридной частотой.
Показано, что для спектральной зависимости сечения фотоионизации в случае поперечной поляризации света характерен квантово-размерный эффект Зеемана. Промежутки между пиками в дублете Зеемана заполнены осцилляциями интерференционной природы, период которых экспоненциально возрастает с уменьшением расстояния между 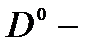 центрами и незначительно меняется с ростом магнитного поля.
центрами и незначительно меняется с ростом магнитного поля.
6. Показано, что расстояние между резонансными пиками, составляющими дублет Зеемана, определяется циклотронной частотой, а дублеты расположены на кривой поглощения с периодом, определяемым гибридной частотой.
Дата добавления: 2021-07-19; просмотров: 125; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
