Водородоподобные примесные центры в наноструктурах

Рассмотрят водородоподобный (кулоновский) примесный центр в объемном материале. Взаимодействие электрона и примесного иона во многих случаях может быть описано кулоновским потенциалом:

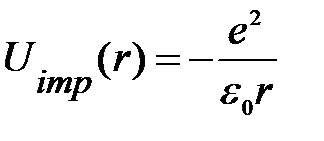                                                               (1.1.1)

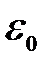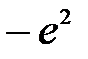где  статическая диэлектрическая проницаемость материала,  расстояние до примесного центра; начало координат помещено  в   центр     примесного   иона. Величина  представляет собой произведение заряда электрона на заряд иона, который здесь полагается равным по величине и противоположным по знаку заряду электрона. 

Если принять, что электронные состояние в зоне проводимости полупроводника описываются в рамках метода эффективной массы в однозонной изотропной модели, то уравнение Шредингера для волновых функций 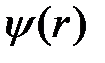 и уровней энергии Е стационарных состояний электрона в потенциале (1.1) запишется в виде:

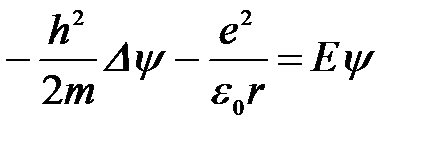                                                         (1.1.2)

где m – эффективная масса электрона, 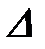 – оператор Лапласа.

Это уравнение подобно по своей форме уравнению Шредингера для электрона в атоме водорода и отличается от него только заменой массы 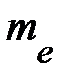 электрона в вакууме на эффективную массу m электрона полупроводнике, а также заменой квадрата заряда электро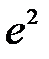на   на . Поэтому можно воспользоваться известным решением для атома водорода [4], произведя в нём указанную замену. Волновые функции стационарных состояний в сферической системе координат имеют вид произведения радиальной и угловой функций:

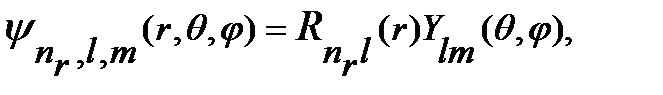                          (1.1.3)

где 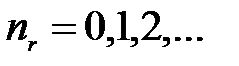– радиальное квантовое число (оно равно количеству узлов радиальной функции  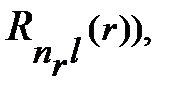l= 0, 1, 2, ... – орбитальный момент импульса (в единицах 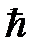), m=l,  l –1, ... , –l – проекция момента на ось z. Уровни энергии не зависят от квантового числа m (его не следует смешивать с массой электрона), то есть они (2l+1)-кратно вырождены по m, причём от квантовых чисел nr  и l уровни энергии зависят только через сумму

                                                (1.1.4)

называемую главным квантовым числом:

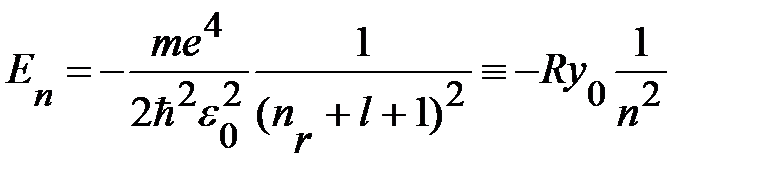                             (1.1.5)

Здесь 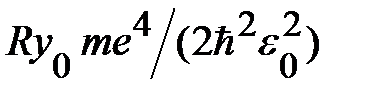–  эффективная постоянная Ридберга; её величина может быть существенно меньшей, чем величина постоянной Ридберга для атома водорода 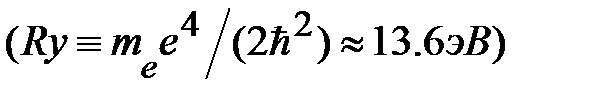, постольку в полупроводнике обычно 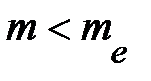и .

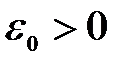Примесные уровни (1.1.6) расположены в запрещённой зоне, ниже края зоны проводимости, выбранного за начало отсчёта энергии. Каждому уровню 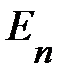(c n > 1) принадлежит  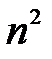состояний (1.1.4), различающихся значениями квантовых чисел. С учётом спина кратность вырождения уровней E_n увеличивается вдвое и составляет уже 2n ².

Обычно главную роль играет основное состояние – обладающее наименьшей энергией. Волновая функция (1.1.4) в случае основного состояния соответствует квантовым числам n_r = 0, l = 0, m = 0; она имеет сферическую симметрию и описывается формулой:

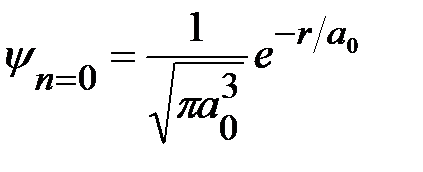                                          (1.1.6)

где величина

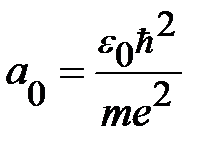                                                     (1.1.7)

 

называется эффективным боровским радиусом. Как видно из выражения (1.1.7), 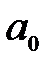имеет смысл радиуса локализации примесного состояния. Энергия основного состояния ( 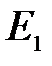) равна

.                                        (1.1.8)

Её абсолютная величина, 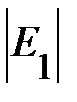, представляет собой энергия связи электрона на примесном центре.

Приведен количественный пример. Для GaAs: , ,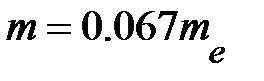поэтому 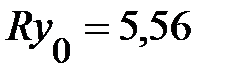мэВ и 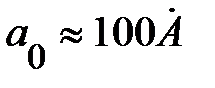. Поскольку глубина залегания примесного уровня  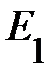оказывается малой по сравнению с шириной запрещённой зоны, примесный уровень называют мелким; примесные состояния в этой задаче получили название «водородоподобных» состояний.               

Здесь были рассмотрены задачу о водородоподобном примесном центре полупроводнике, имеющем форму тонкой плёнки, или тонкого слоя в составе полупроводниковой гетероструктуры. Если               величина диэлектрической проницаемости пленки отличается от диэлектрической проницаемости подложки и вакуума, то границами привносятся силы изображения, которым соответствует некоторая добавка к кулоновскому потенциалу (1.1.1). В гетероструктурах различия в значениях диэлектрической проницаемости слоёв обычно незначительны, и вкладом в потенциал от сил изображения можно пренебречь.

Но и в отсутствие сил изображения энергия электрона на примесном центре в квантовой яме может отличаться от энергии примесного состояния в объемном образце: если расстояние между интерфейсами гетероструктуры не превышает эффективного  боровского радиуса, то к кулоновскому потенциалу в уравнении (1.1.2) добавится    «потенциал    конфайнмента» 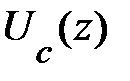, характеризующий рельеф дна зоны проводимости. Кроме того, энергия связи должна зависеть от того, насколько близко к интерфейсу расположен примесный центр. Полагая, как обычно, что ось z направлена по нормали к плоскости интерфейсов гетероструктуры, следует в общем случае вместо (1.1.2) записать уравнение Шредингера с потенциалом  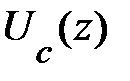и с кулоновским потенциалом , зависящим от координаты примесного центра :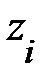

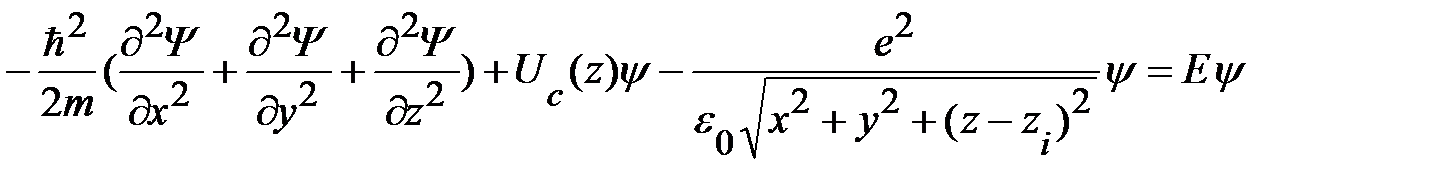.       (1.1.9)

Здесь считается, что начало координат в плоскости (x, y) помещено в центр примесного атома, и что различные положения примеси в плоскости (x, y) эквивалентны в силу трансляционной симметрии гетероструктуры в направлениях x, y.

В случае ступенчатого потенциала  волновая функция на границах слоёв должна подчиняться определённым условиям непрерывности. На первый взгляд, самая простая задача этого типа возникает в случае прямоугольной потенциальной ямы с бесконечно высокими барьерами:

                                 (1.1.10)

где L – ширина квантовой ямы. В такой задаче на волновую функцию налагается условие обращения в ноль на стенках ямы (а также всюду вне ямы):

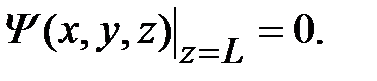                                         (1.1.11)

Однако даже в этой сильно идеализированной модели получить точное решение при общих условиях невозможно. Это удаётся сделать только в предельном случае, когда ширина квантовой ямы мала по сравнению с эффективным боровским радиусом:

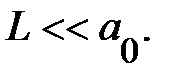                                    (1.1.12)

Рассмотрят случай (1.1.13) подробно. Можно ожидать, что в направлении осей x и y (точнее, в любом направлении в плоскости ямы) волновая функция примесного состояния 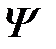 заметно отличается от нуля на расстояниях от начала координат порядка 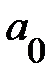. Поэтому характерный масштаб значений x и y в выражения для кулоновского потенциала имеет порядок 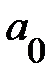. Однако существенные значения координаты  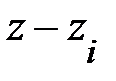в силу граничных условий (1.1.13) это означает, что в выражения для кулоновского потенциала можно пренебречь величиной 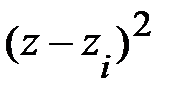, малой по сравнению с , так что (1.1.10) примет вид уравнения с разделяющимися переменными z и (x, y):

 

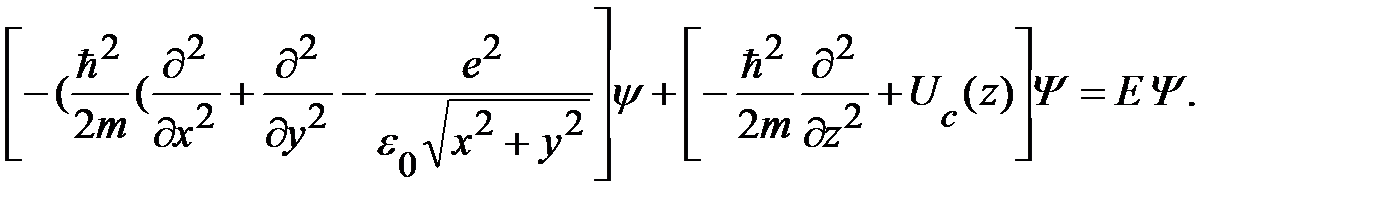(1.1.13)

Применяется к (1.1.14) стандартный способ разделения переменных, то есть будят искать решение 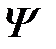 в форме произведения новых неизвестных функций:  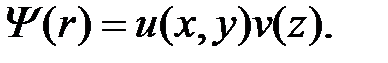Тогда (1.1.14) сводится к двум независимым уравнениям:

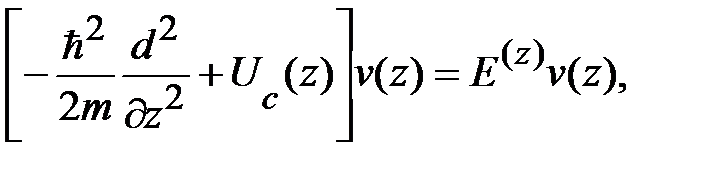                            (1.1.14)

 

               (1.1.15)

где

 

.                                           (1.1.16)

 

Решения уравнения (1.1.12) при учёте граничных условий (1.1.12) и прямоугольной формы потенциала (1.1.11) представляют собой хорошо известные одномерные состояния в потенциальной яме с бесконечными барьерами:

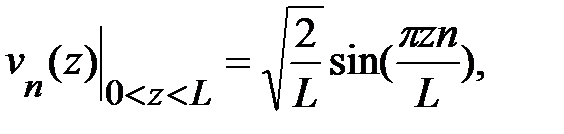
,        (1.1.17)

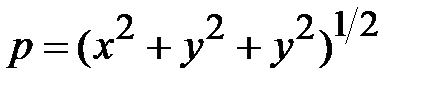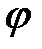Уравнение (1.1.15) также является относительно простым; решение имеется в задачниках по квантовой механике, и мы воспроизводим его ниже. Перейдем от  декартовых  координат  x  и  y  к  полярным координатам  и , так что 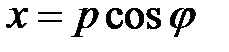, 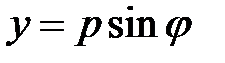.  Тогда 

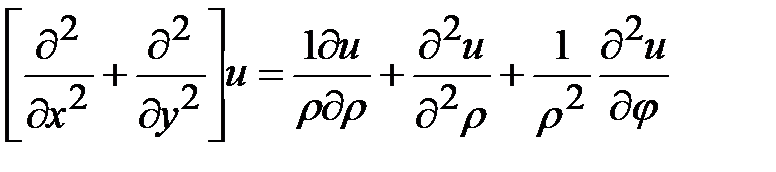,                     (1.1.18)

и  в   уравнении (1.1.16) можно   произвести дальнейшее разделение переменных. Положили, что 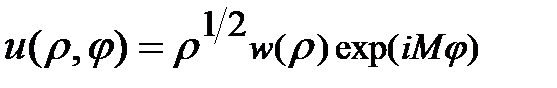, где для однозначности волновой функции u необходимости, чтобы квантовое число M было целым:

                                       (1.1.19)

Тогда (1.1.16) сводится к уравнению для неизвестной радиальной функции 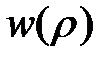 в нашей двумерной задаче:

.         (1.1.20)

Сравнять (1.1.21) с уравнением для радиальной волновой функции R(r) в трёхмерной    задаче (1.1.2). С учетом того, что 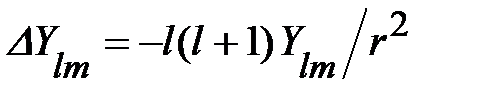, задача (1.1.20) после разделения переменных в  сферических координатах приводится к уравнению        

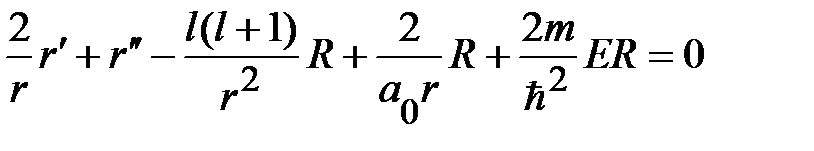                (1.1.21)

При E < 0 требование     ограниченности функции R(r) удовлетворяется только для дискретных значений E – так возникает результат (1.1.5). Замечено  здесь, что замена r на 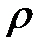 и   на 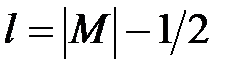 переводит уравнение (1.1.22) в уравнение (1.1.22) для волновой функции w, и функция w тоже должна удовлетворять условию ограниченности.    Следовательно, дискретный спектр задачи (1.1.21) можно найти просто подстановкой  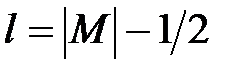в формулу (1.1.5):

.                          (1.1.22)

Здесь квантовое число =0,1,2, … интерпретируется как число узлов у решения 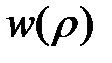; это продиктовано известной в квантовой механике «осцилляционной теоремой», которая устанавливает соответствие между количеством узлов собственной функции и номером собственного значения. Квантовое число  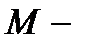проекция орбитального момента на ось z; закон сохранения этой проекции момента обусловлен аксиальной симметрией двумерной задачи (1.1.16). Наименьшему значению энергии (1.1.23) соответствуют 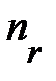= 0 и  так что:

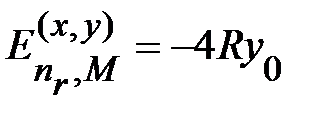.                                           (1.1.23)

Уровень ближайшего   возбуждённого состояния, 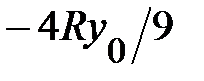, трёхкратно вырожден, поскольку ему отвечают три разных значения пары квантовых чисел ; это (0,–1), (0,1) и (1,0). Если по аналогии с (1.1.4) ввести «главное» квантовое    число N = 1,2,… , нумерующее уровни (1.1.23) в порядке их возрастания, то кратность вырождения N-го уровня будет равна  2N – 1. При этом число N выражается через квантовые числа  формулой

,                                                (1.1.24)

а энергия примесных состояний (1.1.23) запишется в виде:

 

, =1,2, …                    (1.1.25)

Наконец, с учетом (1.1.17) – (1.1.18) окончательное выражение для уровней энергии примет вид:

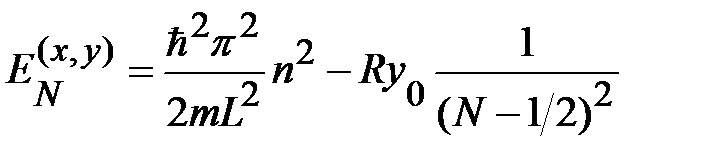.                         (1.1.26) 

Таким образом, под каждым уровнем размерного квантования (с заданным n) примесный центр создаёт водородоподобную серию уровней с различными значениями N. Все примесные уровни являются «мелкими» по отношению к интервалам 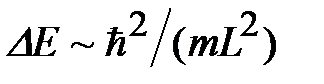 между  под зонами  размерного квантования; действительно, 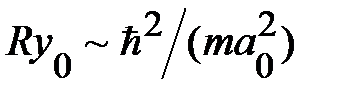, поэтому из неравенства (1.1.13) следует, что 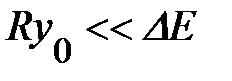. Отсюда следует также, что все примесные уровни, кроме тех, которые находятся под самой нижней подзоной, расположены на фоне энергетических ветвей других под зоны; значит, эти примесные состояния могут «распадаться» в состояния под зоны, то есть эти примесные уровни энергии имеют конечную ширину. Согласно формуле (1.1.24) в двумерной системе энергия связи электрона на кулоновском примесном центре в четыре раза больше, чем в трёхмерном случае. Такое значительное увеличение энергии связи объясняется   тем, что стенки ямы шириной 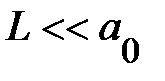не позволяет электрону удаляться от примесного иона в направлении оси z, и энергия притяжения поэтому возрастает. В модели (1.1.11) – (1.1.13) не удается изучить зависимость энергетических уровней и волновых функций примесных состояний от ширины квантовой ямы, от высоты потенциальных барьеров, от отношения эффективных масс или диэлектрических проницаемостей слоёв. Подробное исследование требует численных расчётов; которые чаще всего выполняются вариационным методом с той ли иной пробной функцией, моделирующей свойства локализованных на примеси состояний. Тем не менее, в поведении примесных состояний можно отметить ряд качественных черт [7].

Так, очевидно, что при большой ширине 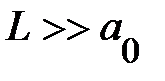 квантовой ямы B/A/B, примесные уровни центра, расположенного вблизи середины ямы, будут такими же, как у примеси, расположенной в объёмном материале A. С уменьшением ширины А-слоя волновая функция электрона на примесном центре начинает «сдавливаться» стенками  ямы,  что  ведёт  к  возрастанию  энергии  притяжения электрона к примеси, и энергия связи будет больше, чем 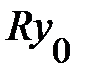в объёмном материале А. В случае бесконечно высоких барьеров энергия связи при  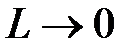монотонно возрастала бы до значения  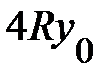(а уровень размерного квантования поднимался бы по шкале энергии до бесконечности). Однако в случае барьеров конечной высоты уменьшение ширины A-слоя приводит к тому, что уровень размерного квантования поднимается до уровня барьера В-слоёв, и волновые функции как размерно-квантованных состояний, так и примесных проникают в материал барьеров на всё бóльшую глубину; такое ослабление конфайнмента проиллюстрировано на рисунке 3.

Когда длина конфайнмента становится больше, чем радиус локализации 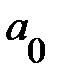 примесного состояния, стенки ямы мало влияют на энергия связи электрона с примесью. В пределе с  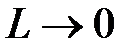слой А параметрами материала В. Энергия связи при этом будет равна эффективной постоянной Ридберга с эффективной массой электрона m и диэлектрической проницаемостью в материале В.

 

Рисунке – 3. Увеличение длины локализации связанного состояния при уменьшении ширины квантовой ямы конечной глубины. [https://elib.spbstu.ru/dl/2375.pdf/download/2375.pdf].

 

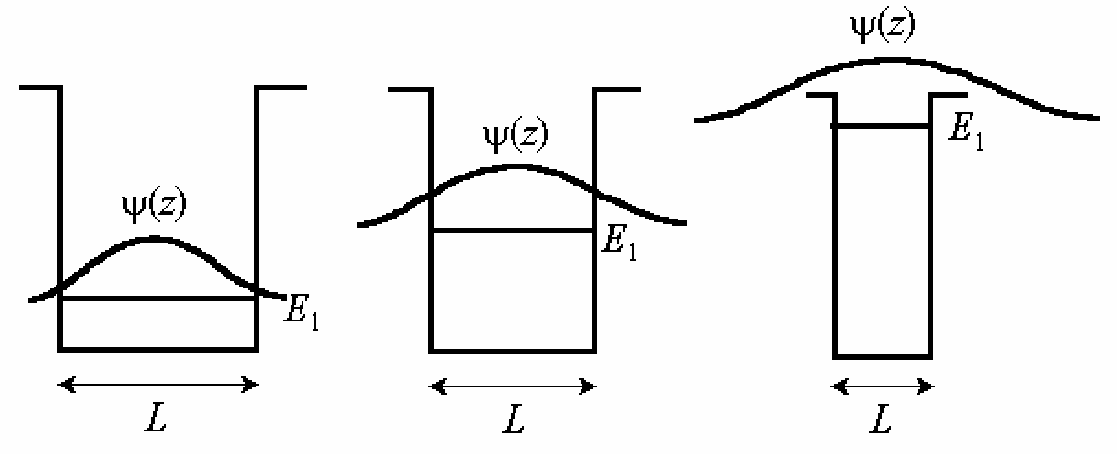
Таким образом, с уменьшением ширины ямы, имеющей барьеры конечной высоты, от больших значений ( 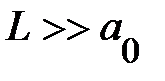) до малых ( 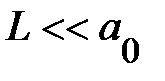)энергия связи электрона на примеси сначала возрастает от значения  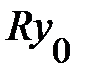в материале А до максимального значения, сравнимого с 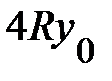, а затем уменьшается до значения 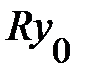в материале В см. рисунке 4.

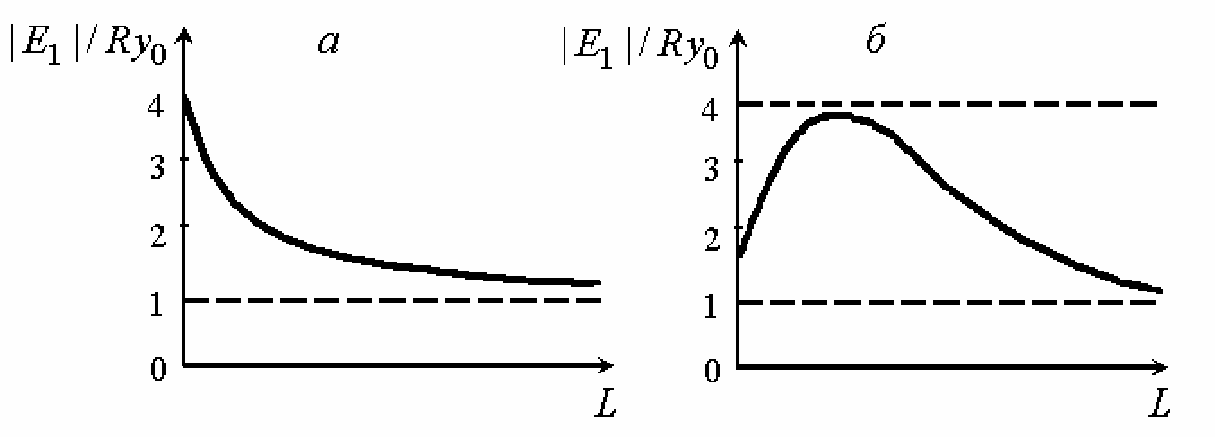
Рисунке 4. Зависимость энергии связи электрона на примесном центре от ширины квантовой ямы (схематично). а – в случае ямы с бесконечно высокими стенками, б – со стенками конечной высоты[https://elib.spbstu.ru/dl/2375.pdf/download/2375.pdf].

 

 

Энергия связи примесного состояния зависит не только от ширины квантовой ямы, но и от положения 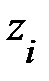примесного центра по отношению к стенкам ямы.

 

Рисунке 5. Изменение формы волновой функции примесного состояния в зависимости от положения атома примеси относительно центра широкой ( L>> a₀ ) квантовой ямы;

[https://elib.spbstu.ru/dl/2375.pdf/download/2375.pdf].

 

   Влияние положения примеси на форму волновой функции основного состояния в широкой квантовой яме схематично показано на рисунке 5. Расчёты показывают, что в центре ямы энергия связи больше, чем у ее края, то есть у края ямы уровень энергии примесного состояния расположен выше, чем в центре. Это можно объяснить увеличением кинетической энергии электрона в примесном состоянии, «прижатом» к стенке ямы. Действительно, из соотношения неопределённости Гейзенберга следует, что локализация электрона на интервале 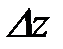 ведёт к неопределённостиимпульса 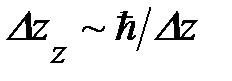, которая даёт вклад в кинетическую энергия порядка 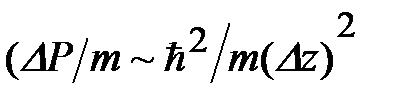. Чем меньше интервал 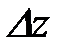, занимаемый электронным «облаком», тем выше энергия данного состояния. При уменьшении ширины ямы L этот эффект повышает не только энергию примеси, но и уровни размерно-квантованных состояний в под зонах.

 

Интерфейсные дефекты

Предполагается , что интерфейс гетероструктуры представляет собой плоскость, лишённую дефектов. На практике всегда имеются несовершенства интерфейса, которые, как и примесные центры, приводят к появлению локализованных (связанных) электронных состояний. Такие дефекты, в частности, могут иметь вид выступов на плоскости интерфейса, обусловленных локальным проникновением материала из B-слоя на некоторую глубину в материал А, или наоборот. Здесь рассмотрят, следуя [6], схему вариационного расчёта энергии связанных состояний на дефекте, поскольку она иллюстрирует общий подход к приближённому количественному описанию дефектов различного типа.

Уравнение Шредингера для электронных состояний в гетероструктуре с интерфейсным дефектом можно записать в форме (1.1.10), заменив кулоновский потенциал примеси потенциалом дефекта в общем виде, :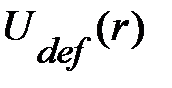

 

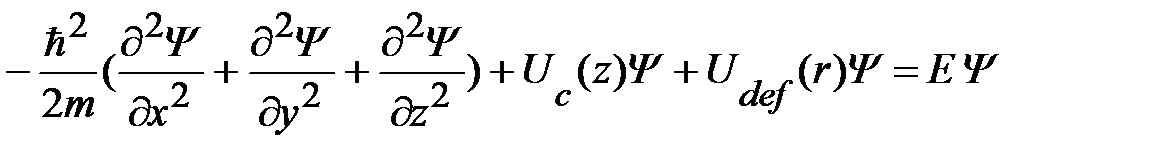.           (1.2.1)

Операторные слагаемые в   гамильтониане этого уравнения можно перегруппировать так, что уравнение примет вид

 

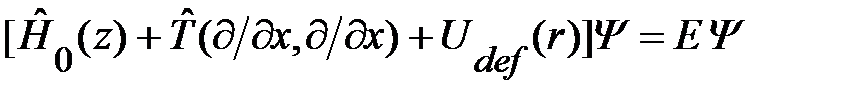,                (1.2.1)

где

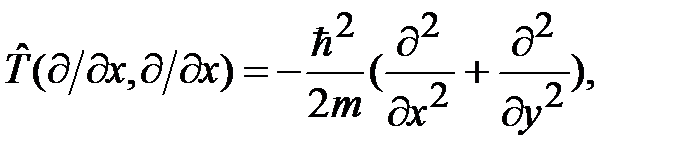                        (1.2.3)

 

.                              (1.2.4)

Здесь 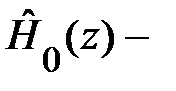одномерный гамильтониан гетероструктуры с идеальными интерфейсами, например квантовой ямы с профилем зоны проводимости . Его собственные значения – обычные уровни размерности квантовая для движения электрона вдоль оси z.

Предложили, что ортонормированные собственные функции 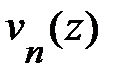 и собственные значения энергии 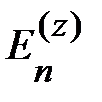для гамильтониана  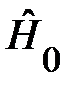уже найдены:

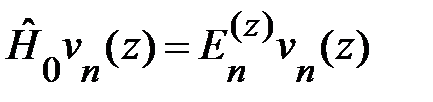.                                    (1.2.5)

Искали решение уравнения (1.2.5) в виде:

 

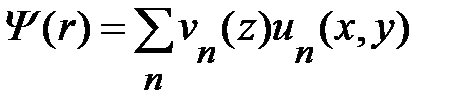.                                (1.2.6)

Подставляя (1.2.7) в (1.2.4) и учитывая (1.2.6), получили:

.                (2.7)

 

Умножили обе стороны уравнения (1.2.8) на 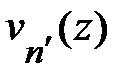 и проинтегрируем по z, учитывая условие ортонормировки функций 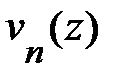, имеющие вид:

 

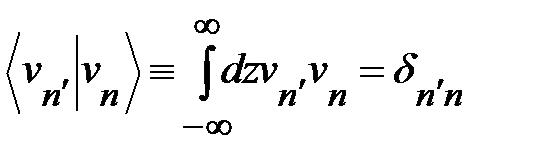                               (1.2.8)

Получим:

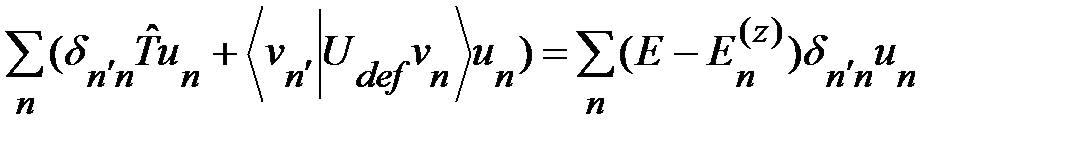.       (1.2.9)

Предположили что потенциал  не смешивает состояния с разными n, то есть можно пренебречь недиагональными членами:

,      (1.2.10)

где эффективный потенциал дефекта 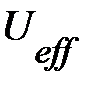 определён выражением:

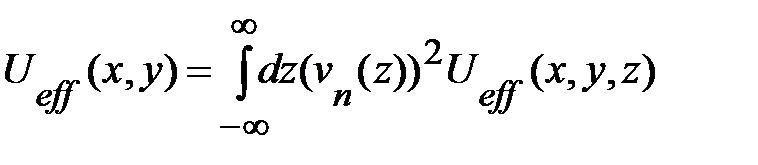.                   (1.2.11)

Тогда, выполнив в (1.2.35) суммирование и заменив индекс  на n, придём к уравнению Шредингера для волновой функции ,описывающей движение электрона на n-ом размерно-квантованном уровне вдоль плоскости интерфейсов с учётом эффективного потенциала дефекта:

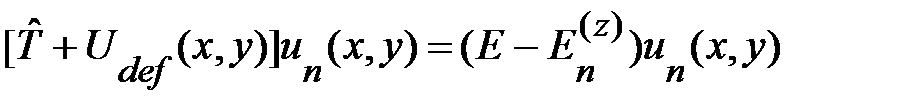.                   (1.2.12)

Обычно рассматривают нижний уровень, n = 1, и интересуются связанными (локализованными) состояниями под этим уровнем, как в задаче о водородоподобной примеси. Если такие состояния для выбранной модели дефекта существуют, то энергия E основного состояния должна быть меньше, чем 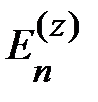, и её можно оценить вариационным методом. С этой целью выбирают в явном виде пробную волновую функция должна убывать до нуля с ростом своих аргументов x и y. Если умножить обе стороны уравнения (1.2.13) с n=1 на 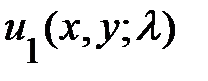 и проинтегрировать по x и y, то получим:

, то есть 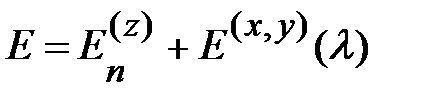,             (1.2.13)

где

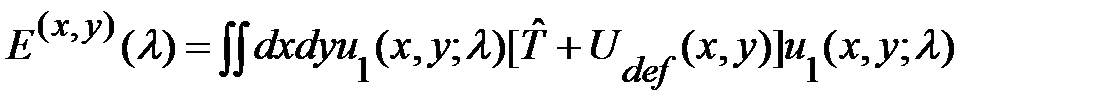.       (1.2.14)

В  завершение    процедуры     следует решить  уравнение 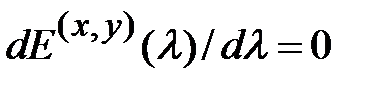, которым определяется значение 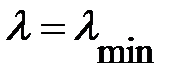, доставляющее минимум энергии (1.2.14). Если для конкретной модели дефекта  вариационная  процедура  приводит  к  результату 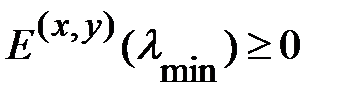, это ещё не означает отсутствия связанного состояния, так как вариационный метод даёт значение энергии, которое является оценкой сверху для истинной энергии основного  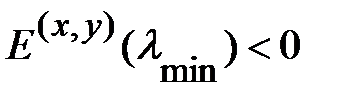величина  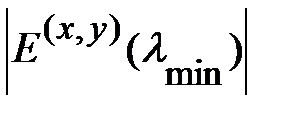интерпретируется как правдоподобная оценка энергии связи электрона на дефекте. Таким методом можно изучить энергетический спектр электрона на интерфейсных дефектах различных размеров и типов.

 

 

УРОВНИ ЭНЕРГИИ ЭЛЕКТРОНОВ

---

Дата добавления: 2021-07-19; просмотров: 153; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!