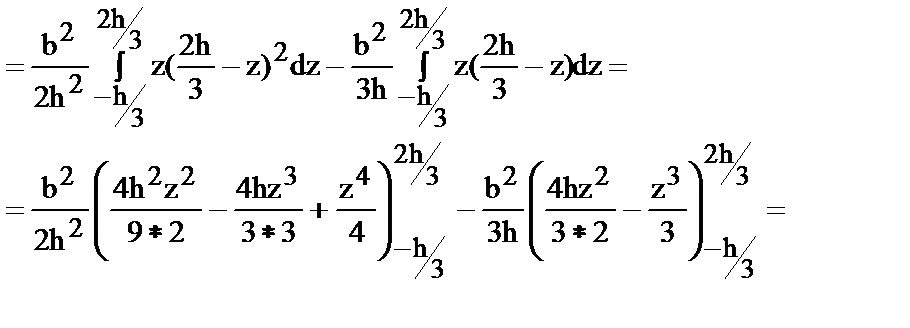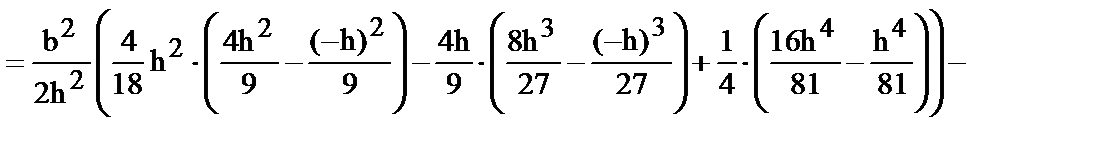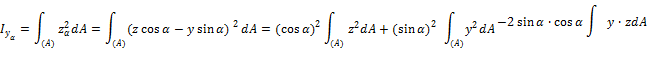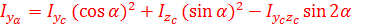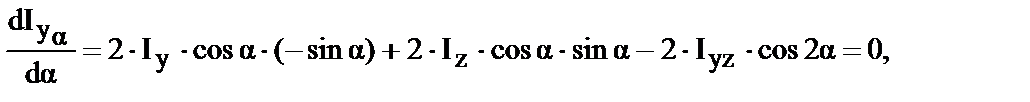Определение центра тяжести сечения и положения центральных осей
Геометрические характеристики сечений
§1. Моменты инерции простых фигур
| Рис. 1 |
При решении задач Строительной механики появляется ряд коэффициентов, выраженных в интегральной форме, которые не имеют явно выраженного физического смысла как, например площадь сечения или объем тела. Одно такое выражение ранее назвали статическим моментом площади. Подынтегральные выражения здесь представляются в виде произведения площади на расстояния до осей. Здесь вводится новое понятие, интегральная функция, в которой подынтегральное выражение представляются в виде произведения площади на квадраты расстояния до осей. Вот эти выражения.
Интеграл вида
 (1)
(1)
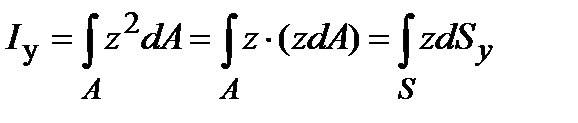
|
называется моментом инерции сечения относительно оси у, а выражение
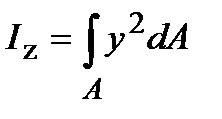 (2) (2)
|

|
называется моментом инерции сечения относительно оси z.
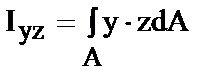
| (3) |
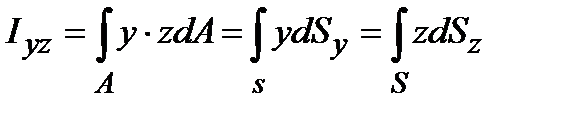
|
центробежный момент инерции сечения относительно осей y и z, а
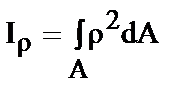
| (4) |
полярный момент инерции.
Поскольку r2=y2+z2 , то

| (4a) |
здесь переменные y, z, r - координаты цента тяжести площади элемента dA.
Единица измерения момента инерции: длина в четвертой степени (см4 , м4).
Все эти интегралы появляются как некоторые обобщенные коэффициенты пропорциональности при определении напряжений и деформаций при изгибе и кручении. Они не имеют физического смысла, но имеют аналогию по форме записи с выражением инерции массы, отсюда их название "моменты инерции сечения".
|
|
|
Вычислим моменты инерции некоторых сечений
1. Прямоугольник
|
Рис.2 |
Определим моменты инерции прямоугольника (рис.2) относительно осей z и у Вырежем полоску параллельно оси у высотой dz и вычислим интеграл (1), учитывая что
dA=b×dz
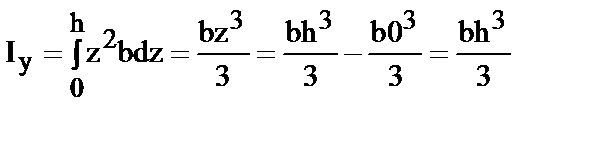
| (5) |
|
Рис. 3 |
Для вычисления интеграла (2) очевидно полоску нужно вырезать параллельно оси z (рис.3) и подставить dA=h×dy

| (6) |
Вычислим центробежный момент инерции (3). По определению центробежный момент инерции это интеграл от произведения элементарной площадки на расстояния до осей и поэтому
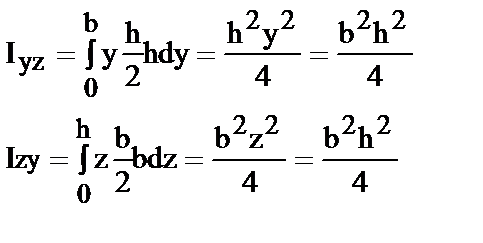
| ((7) |
Вычислим те же моменты инерции относительно осей, проходящих через центр тяжести (центральных осей) (рис.4).
|
Рис.4 |
По аналогии
|
| (8) | |
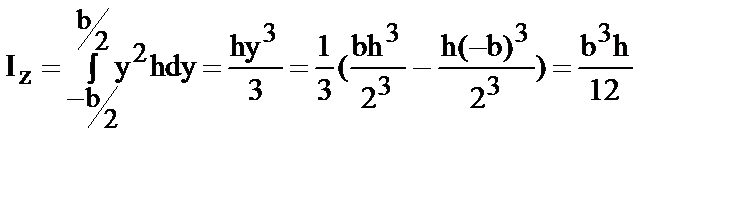
|
(9) | |
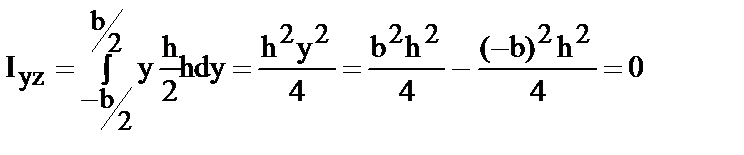
| (10) |
Центробежный момент может быть отрицательным, а осевые моменты инерции всегда положительные. Этоследует из самих интегралов: четные и нечётные степени переменных интегрирования.
2. Прямоугольный треугольник
Рис.6
Как и в предыдущей задаче вырежем полоску высотой dz (рис.6b) и найдем её площадь
|
|
|
dA=bz×dz
bz - ширина полоски определится из подобия треугольников
bz./b = (h-z)/h Þ bz= b×(h-z)/h
dA = b×(h-z)/h×dz.
В соответствии с (1)
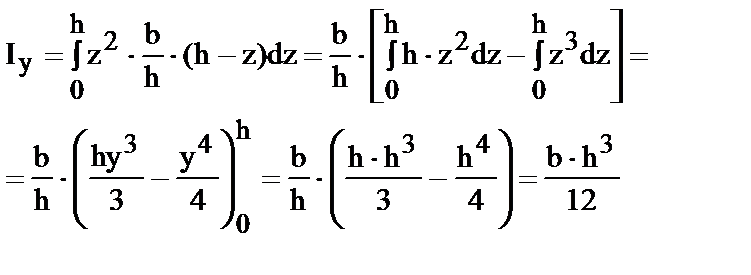
| ((12) |
Аналогично, вырезая полоску параллельно оси у, получим
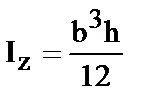
| (12,a) |
Для центробежного момента инерции следует иметь ввиду, что координата центра тяжести элементарной площадки y=bz/2.
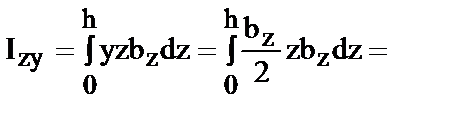    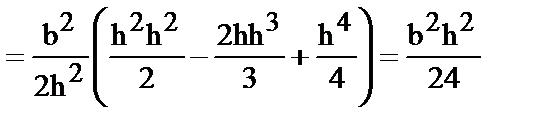
| (13) |
Для центральных осей (рис.6,с)
bz/b= (2h/3-z)/h Þ bz=b×(2h/3-z)/h
dA = b×(2h/3-z)/h×dz
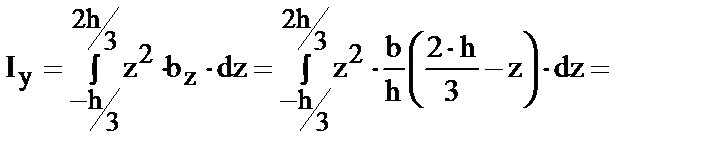 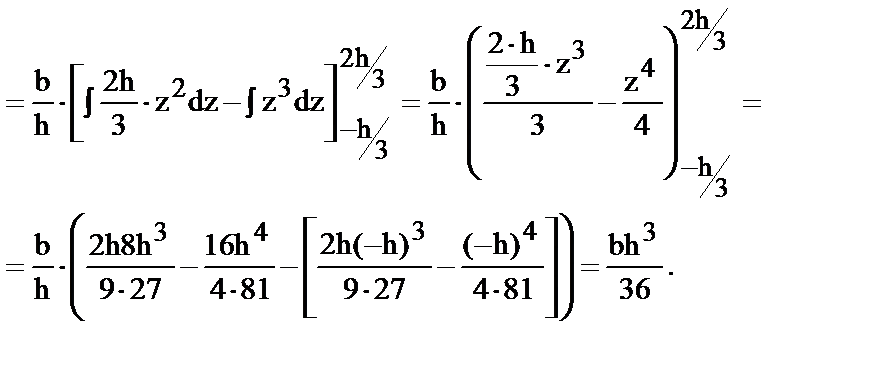
| (14) |
по аналогии

| ((15) |
Для определения центробежного момента инерции относительно центральных осей воспользуемся координатами центра тяжести элементарной площадки dA: z и y=bz/2-b/3, где b/3 - смещение новых осей относительно старых по оси y.
 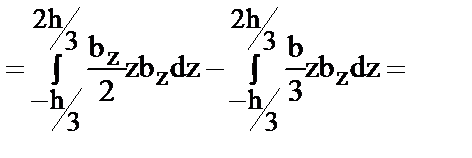
|
|
| |

| (16) |
Обратите внимание! Центробежный момент инерции отрицательный, когда большая часть площади треугольника при центральных осях находится в квадрантах с разнозначными ветвями осей, а это происходит тогда, когда по гипотенузе опускаемся от положительного конца ординаты к положительному концу абсциссы или от отрицательного конца абсциссы к отрицательной ветви ординаты.
|
|
|
Круг
| Рис. 7 |
Вычислим полярный момент инерции (4) круга (рис. 7). Выделим элементарную площадку в виде кольца шириной dr
dA=p(r+dr)2-pr2=p(2rdr+dr2)=2prdr,
так как
dr2<<rdr.
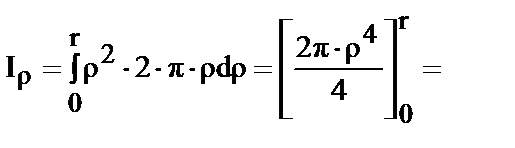 
| (17) |
Тогда

| (6.18) |
Для круга очевидно Iz=Iy,учитывая (17) и (4a), найдём:
4.Моменты инерции четверти круга
1. Моменты инерции относительно осей Y,Z
| Рис.8 |
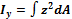 ;
;
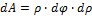
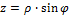
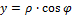


Подставляются пределы интегрирования:
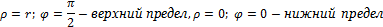
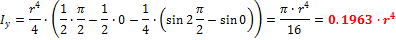
Из (6.18) следует
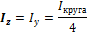
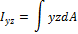

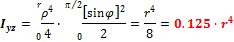
В первой и третьей четверти центорбежные моменты инерции положительные, во второй и четвёртой отрицательные и тогда суммируя их, получим центробежный момент инерции круга Он равен нулю.
2. Моменты инерции относительно центральных осей Yc,Zc
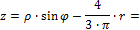
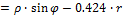
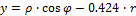
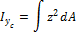
| Рис .8а |

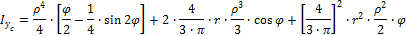
Подставляются пределы интегрирования:
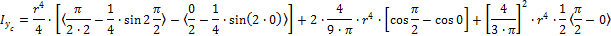
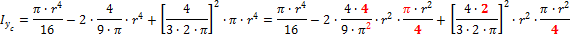


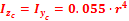
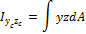
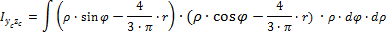
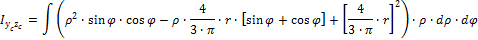
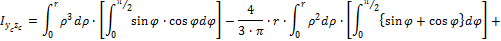
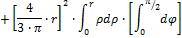
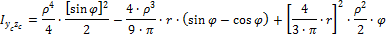
Подставляются пределы интегрирования:
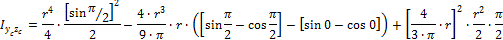

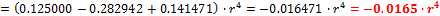
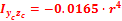
3. Момент инерции относительно осей Y2, Z2

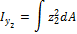

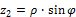
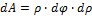
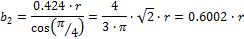

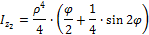
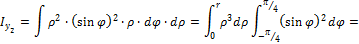

переходя к пределам интегрирования, получаем
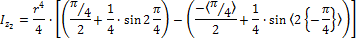
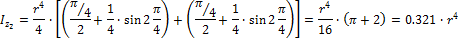
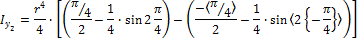
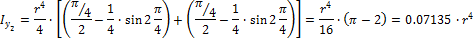
§2. Моменты инерции сложных сечений
Выражения значений моментов инерции могут быть получены для достаточно простых фигур (рис.2-8). А как быть, если сечение представляет более сложную фигуру?
|
|
|
Рассмотрим сечение (рис.6.8) и вычислим осевой момент инерции относительно ост Y.
| Рис.9 |
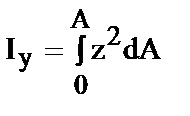
Представим сечение в виде совокупности простых сечений, площади и моменты инерции которых легко определяются
Пусть 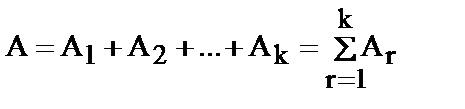 ,
,
тогда учитывая свойства определенного интеграла, запишем
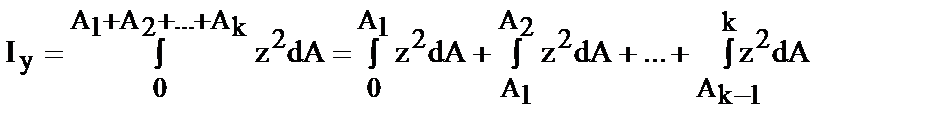
Но каждый из интегралов - это момент инерции какой-то фигуры, составляющей часть сечения, следовательно
 , ,
| (19) |
§3. Моменты инерции сечений относительно параллелельных осей
| Рис.10 |
Пусть имеется две пары координатных осей Y1О1.Z1 и YIIОII.ZII (рис.6.10) координаты центра О2. в системеyIOIzIравны:
Координаты точки К в системе yIОI.zI: {y1,z1.}
| y12.=a;z12=b | (20) |
в системе yIIОIIzII:.{y2, z2.} с учетом (6.20)
| y2=y1-a; z2=z1-b. | (21) |
Моменты инерции в системе .yIIОII.zII
Iy2=ò (z2)2dA Iz2=ò (y2)2dA.
Подставим (6.21)
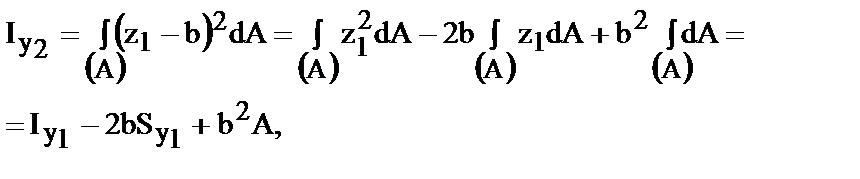
| (22) |
где - 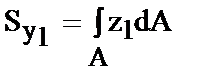 статический момент сечения. Пусть оси yIОI.zIбудут центральными, тогда Sy1.=0 и
статический момент сечения. Пусть оси yIОI.zIбудут центральными, тогда Sy1.=0 и
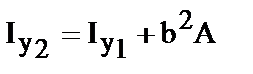
| (23) |
или
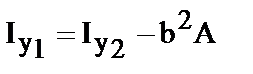
| (24) |
Обратите внимание: момент инерции относительно центральной оси (24) всегда меньше момента инерции относительно любой другой ей параллельной (23); поскольку по определению Iy1.>0 из (6.24) также следует что Iy2.> b2×A.
Для других моментов инерции:
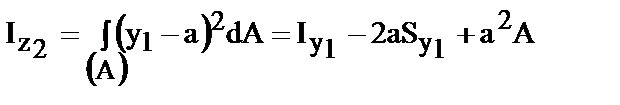 ; ;   =
= 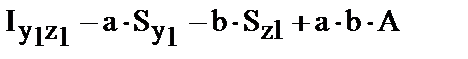
| (25) (26) |
и если оси yIОI.zI являются центральными осями, то

| (27) |

| (28) |

| (29) |
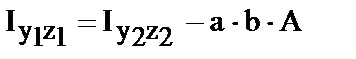
| (30) |
Из анализа результатов этого параграфа можно сделать такой вывод:
Для определения момента инерции сечения относительно любой оси необходимо знать соответствующие моменты инерции этого же сечения относительно центральной оси, параллельной заданной.
§4. Момент инерции относительно повернутых осей
|
Рисунок 12 |
Рассмотрим две пары координатных осей, имеющих общее начало и развернутые относительно друг друга на угол a против часовой стрелки (рис.12). Определим координаты точки K в системе координат YaOZa (показаны зелёным цветом), если ее координаты в системе YOZ соответственно равны yk, zk.
Очевидно, что yak.=KP=OD=OC+CD; из треугольника OAC имеем OC=OA/cosa=yk/cosa; из треугольника CDKÞCD=KC×sina. Определив из треугольника OAC значение CA, получим KC=KA-CA =zk.-yk×tga. Подставим полученные значения в выражение для yak, найдем
| yak.=yk/cosa+(zk.-yk×tga)×sina=(yk-yk×sin2a+zk×cosa×sina)/cosa= =(yk×cos2a+zk×cosa×sina)/cosa =yk×cosa+zk×sina | (32) |
Для другой координаты имеем
| zak=OP=KD=KC×cosa=(zk.-yk×tga)×cosa=zk×cosa-yk×sina (33) | ( |
Тогда запишем
|
| |||
Аналогично
|
| |||
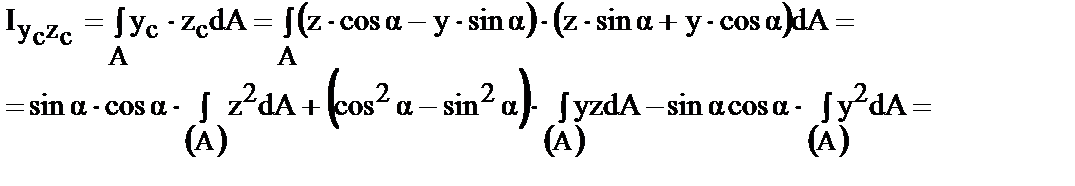 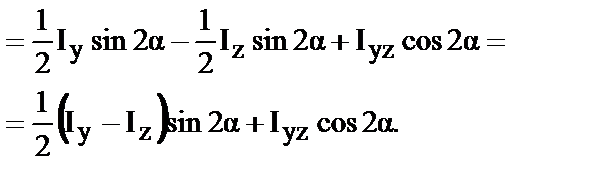
| (36) | ||
Обратите внимание! (34,35,36) дают значение моментов инерции относительно осей повернутых к исходным на угол против часовой стрелки.
Если сложить (34) и (35), то получим доказательство инвариантности суммы моментов инерции относительно любых осей, проходящих через заданную точку

| (37) |
§5. Главные моменты инерции
Из уравнений (34) и (35) очевидно, что  . Меняя угол a, можно получить бесконечное множество пар моментов инерции относительно осей, проходящих через один центр. При этом соблюдается соотношение (37), а значит один момент инерции увеличивается, а другой уменьшается. Поскольку все осевые моменты инерции положительные по определению, то можно предположить, что среди пары моментов инерции есть такая, у которой один момент инерции имеет наибольшее, а другой наименьшее значение, т.е. имеет место соотношение:
. Меняя угол a, можно получить бесконечное множество пар моментов инерции относительно осей, проходящих через один центр. При этом соблюдается соотношение (37), а значит один момент инерции увеличивается, а другой уменьшается. Поскольку все осевые моменты инерции положительные по определению, то можно предположить, что среди пары моментов инерции есть такая, у которой один момент инерции имеет наибольшее, а другой наименьшее значение, т.е. имеет место соотношение:
| Imax.+Imin=Iy+Iz | (38) |
В уравнениях (34,35) в правой части только одна переменная a, а функции I имеют экстремум. Условие экстремальности запишутся следующим образом:
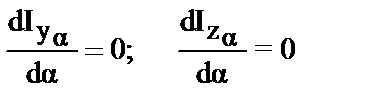
| (39) |
Из этих условий определим угол a, при котором осевые моменты инерции принимают экстремальные значения. Если такой угол существует, то оба соотношения дадут одинаковые значения для угла.
|
| |

| (40) |
|
| |
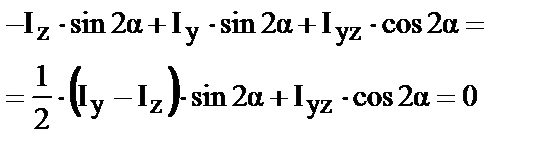
| (41) |
Значение совпали, значит, угол поворота осей, относительно которых моменты инерции достигают экстремума существует.
Оси, относительно которых моменты инерции имеют экстремальные значения, называют главными.
Из (40) и (41) следует:
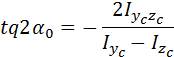 ,
,
| (42) |
где a0 - угол, определяющий положение главных осей в системе координат YOZ.
Сравните левую часть выражений (40) и (41) с правой частью (36). Они одинаковые. Следовательно, относительно главных осей инерции центробежный момент инерции равен нулю.
| Iy0z0 = 0 | (43) |
Если главные оси проходят через центр тяжести сечения, то их называют главными центральными осями инерции.
Выражения (40, 41, 42) никак не связаны с положением начала координат. Следовательно, для каждого сечения можно построить как угодно много главных осей (для каждого начала координат). Однако эти оси не будут параллельны между собой.
Действительно. Пусть в системе координат с началом в точке O моменты инерции имеют значения Iy, Iz и Iyz, а положение главных осей определяется соотношением (42).
Перейдем от системы YOZ к параллельной центральной системе координат Y1O1Z1. Координаты точки O1в системе координат YOZ - a и b. Тогда моменты инерции для новых осей определяются соотношением (6.24), (6.25) и (6.28). Подставив эти значения в формулу (6.42), получим значение угла поворота главных осей в системе Y1O1Z1, как функцию параметров системы YOZ.

| (44). |
Очевидно, что результаты (42) и (44) не одинаковые и следовательно 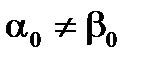
Таким образом для главных моментов инерции из (34 и 35) получим следующие выражения:
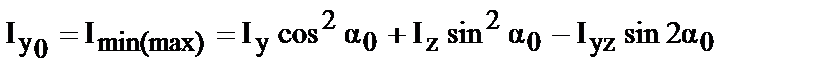
| (45) |
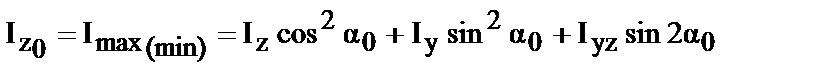
| (46) |
Если в (36) моменты инерции в правой части главные, то есть
Iy=Imax.; Iz=Imin; Iyz.=0,
то тогда центробежный момент для любых осей, повернутых относительно главных на угол a будет определяться соотношением:
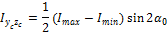
| ((47) |
§6. Радиусы инерции
Выражения
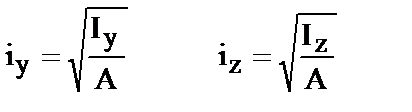
| (48) |
называют радиусами инерции.
| Рис. 6.13 |
Если Y и Z главные оси инерции, то и радиусы инерции тоже главные. На главных радиусах инерции можно построить эллипс инерции, рассматривая их как полуоси. При этом радиус - полуось iy. перпендикулярен к оси Z, а радиус-полуось iz.- соответственно оси Y.
Эллипс инерции, построенный на главных полуосях, имеет несколько прикладных значений:
можно показать, что момент инерции относительно любой центральной оси U равен
| Iu=iu2×A, | (49) |
где iu - расстояние от начала координат до касательной к эллипсу параллельной оси U.
Большая ось эллипса показывает, как надо располагать сечение изгибаемого элемента по отношению к действующим силам. Как станет ясно в дальнейшем, при изучении плоского изгиба, ось должна располагаться в плоскости действия сил.
| Рис. 14 |
Пример 1
!!! Обратите виманиена оси координат. В примере ось Y принята вертикпльной.
Для сечения (рис.14), состоящего из равнобокого уголка N 2.8, равнобедренного треугольника со стороной равной длине полки уголка и полукруга с радиусом равным стороне треугольника найти главные моменты инерции.
Для решения задачи применяется следующий алгоритм
1. Определение положения центра тяжести сечения.
1.1. Запишем координаты центра тяжести каждой простой фигуры и построим для них центральные оси (рис.6.15):
для треугольника координаты центра тяжести О1 относительно катетов имеют следующие значения:
y1=2.8/3=0.933см z1=2.8/3=0.933 см ;
для уголка координаты центра тяжести О2 определяются из сортамента прокатных профилей
y2= z2 =0.8 см
для полукруга координаты центра тяжести О3 относительно осей совпадающих с диаметрами

|
|
1.2. Найдем площади фигур
треугольника
A1=2.8×2.8/2=3.92 см2
уголка (по сортаменту)
A2=1.63 см2
полукруга
A3=p×r2/2==p×2.82/2=12.3 см2
площадь всего сечения
A=A1+A2+A3=3.92+1.63+12.3=17.85см2
1.3. Определяем центр тяжести сечения, используя известные формулы из механики абсолютно твердого тела.
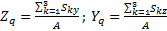 ,
, 
где z и y координаты в осях Z3 и Y3 - глобальной системы координат. Из принятых обозначений следует, что за глобальную систему координат приняты центральные оси полукруга.
Координаты центров тяжести фигур в этой системе координат определятся так
для треугольника:
y13=y1+y3=0.933+1.19=2.12 см; z13=-z1+z3=-0.933+0=-0.933 см
для уголка
y23=y2+y3=0.8+1.19=1.99 см; z23=z2+z3=0.8+0=0.8 см
для полукруга
y33=0; z33=0
Теперь вычислим статические моменты сечения:
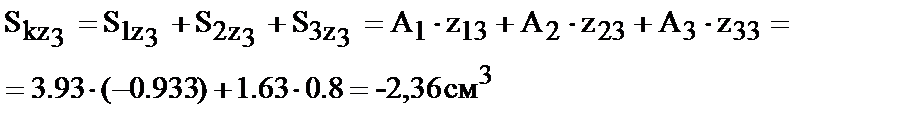
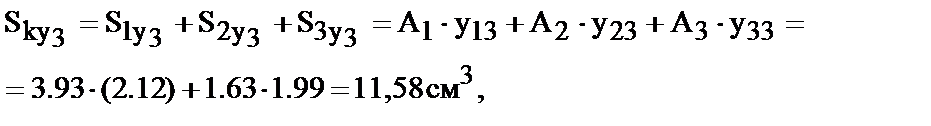 тогда
тогда
z0=-2.36/17.86=-0,132см; y0=11.58/17.86= 0,648см.
Построим центр тяжести сечения O и проведем через него центральные оси сечения Z и Y (рис.15)
2. Определение центральных моментов инерции сечения
2.1. Определим центральные моменты инерции каждой фигуры в собственной центральной системе координат, то есть запишем табличные значения этих параметров.
Для треугольника в соответствии с формулами (14, 15, 16)
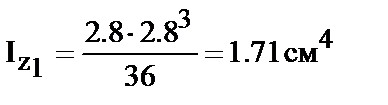
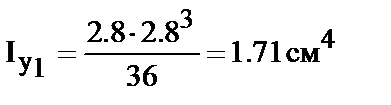
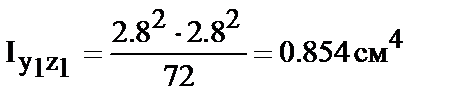
Для уголка определим по сортаменту:
центральные моменты инерции:
Iy2=Iz2=1.16 см4
главные моменты инерции:
Izo2= Imax=1.84 см4.
Из инвариантности моментов инерции (38)
Imin=1.16+1.16-1.84=0.48 см4.
Поскольку уголок равнобокий, то центральные оси инерции Y2 и Z2 повернуты относительно главных на угол a=45°. Тогда центральный центробежный момент инерции равен в соответствии с соотношением (47)
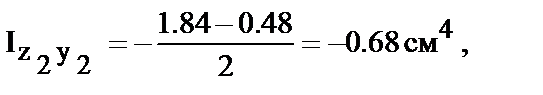
здесь знак минус принят потому, что оси Y2и Z2 повернуты относительно осей YO2 и ZO2 по часовой стрелке (см. замечание выше §4). Отрицательное значение момента инерции очевидно и потому, что большая часть площади уголка находится в квадрантах с разнозначными ветвями координатных осей.
Для полукруга в соответствии с формулой (19) момент инерции относительно оси совпадающей с диаметром полукруга будет равен половине момента инерции круга относительно той же оси
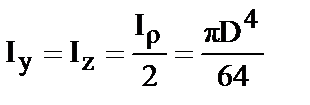 ,
,
тогда Iy3=24.09 см4 , а для определения момента инерции относительно оси Z3 воспользуемся соотношением (24) или (6.28).
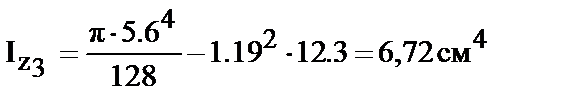
центробежный момент полукруга относительно центральных осей равен нулю, так как они совпадают с его главными осями.
2.2. Определим координаты локальных систем координат каждой фигуры в центральной глобальной системе координат Z и Y
Расстояние между осями Yj и Y
bj=zj-z0.
Расстояние между осями Zi и Z
aj=yj-y0.
подставив в эти соотношения ранее найденные значения координат, получим
| b1=-0.933-(-0.132)=-0.801 см | a1=2.12-0.647=1.47см |
| b2= 0.800-(-0.132)= 0.932 см | a2=1.99-0.647=1.34см |
| b3= 0.000-(-0.132)= 0.132 см | a3=0.00-0.647=-0.647см |
2.3. Вычисление центральных моментов инерции сечения:
По формулам (23, 27, 29 и 19)) находим:
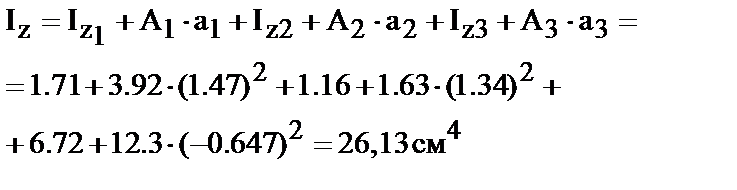
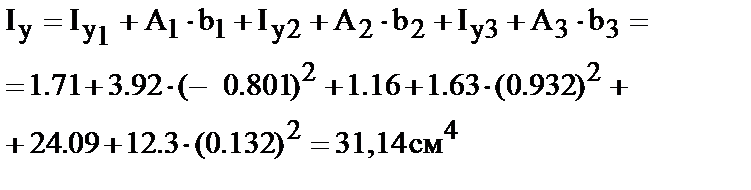
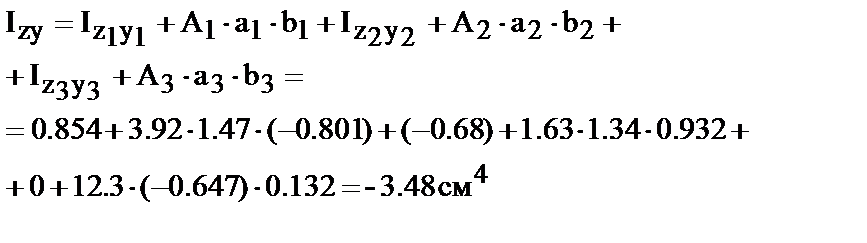
| . 4. Вычисление главных моментов инерции. Воспользуемся уравнениями (45 и 46)
|
3. Определение положения главных центральных осей инерции.
По формуле (42)
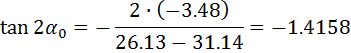
тогда 2a0= -54,77°Þa0= -27.38°
Построим главные центральные оси инерции U и V, повернув центральные оси по часовой стрелке так как угол a0 меньше нуля, а мы использовали уравнение для случая, когда положительный поворот происходит против часовой стрелки
| | 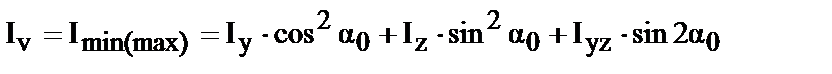
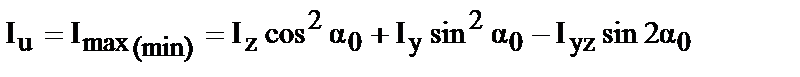
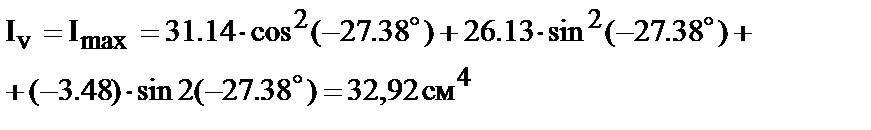
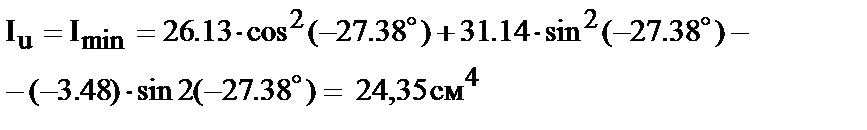
|
5. Определение радиусов инерции.
В соответствии с уравнениями (48)
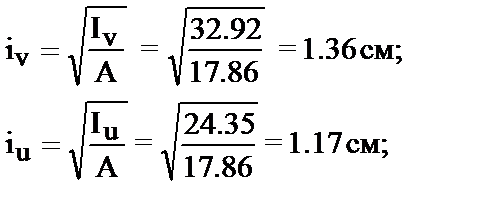
| Рис.17 |
Отложим радиусы перпендикулярно осям, с названием соответствующем индексу радиуса и построим эллипс инерции сечения
.
Из рисунка 17 следует, что балку надо располагать так, чтобы плоскость действия сил совпадала с плоскостью, в которой лежат ось U и продольная ось балки. При загрузке возрастающей центральной сжимающей силой, длинная стойка, имеющая сечение (рис.17) изогнется в направлении оси V. (происходи потеря устойчивости стойки).
Пример 2.
Построить эллипс инерции и определить моменты инерции относительно произвольных центральных осей.
Данные
Двутавр № 40. Из сортамента взяты следующие величины:
Высота 40см, ширина полки 15,5 см.
Площадь сечения А1=72.6 см2 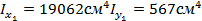
Обратите внимание на соответствие ориентации профиля в задаче и сортаменте
Треугольная пластина
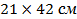 .
.
вычислим параметры, аналогичные параметрам для двутавра.

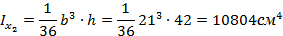
Рис. 18 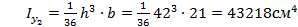

Обратить внимание на знак центробежного момента инерции треугольника. В данном случае он положительный, так как в первом и третьем квадранте находится примерно две трети площади треугольника.
2.2. Площадь сечения

Обозначения.
 центр тяжести фигуры, 1 - двутавр, 2 - треугольник, 0 - всего сечения.
центр тяжести фигуры, 1 - двутавр, 2 - треугольник, 0 - всего сечения.
 центральные оси фигур и сечения: 1 - двутавр, 2 - треугольник, C - всего сечения, 0 - главные центральные оси.
центральные оси фигур и сечения: 1 - двутавр, 2 - треугольник, C - всего сечения, 0 - главные центральные оси.
 - проекция растояния между центрами i-j на ось Y.
- проекция растояния между центрами i-j на ось Y.
Например 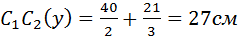 ;
; 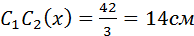
Определение центра тяжести сечения и положения центральных осей
Из теоремы о равнодействующей параллельных сил:
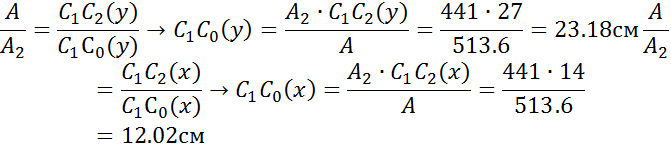
Строятся центральные оси всего сечения Xcи Yc.
Координаты центров тяжести двутавра и треугольника в центральной системе координат соответственно равны:
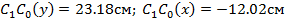

2.4.Определяются центральные моменты инерции:
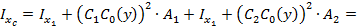

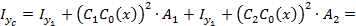
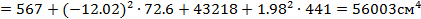
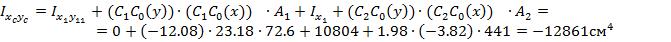
2.5. Определяется положение главных центральных осей:

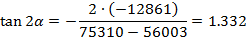
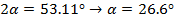
Дата добавления: 2021-03-18; просмотров: 209; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!