Задача (решение с помощью пакета Statistica).

Компания производит электрические компоненты. Для более эффективного по времени производства требуется провести обучение в течение месяца. Поскольку обучающая программа стоит немало средств, руководство компании стремится сократить время на обучение. Руководитель программы изобрел новый метод обучения. Руководство фирмы заинтересовано в проведении специального исследования для того, чтобы определить, сокращает ли новый метод период обучения. Две группы работников по 10 человек обучались с использованием нового метода и стандартного метода соответственно. По окончании периода обучения каждый работник проводил сборку компонента и записывалось время сборки (см. табл.).

МЕТОД	Время, затраченное на производство единицы продукции одним работником, мин.
Традиционный метод обучения, группа 1	32	37	35	28	41	44	35	31	34	30
Новый метод обучения, группа 2	35	31	29	25	34	40	27	32	31	33

Доказывают ли эти данные эффективность нового метода обучения?

14.  Дать пример несмещенной, но не состоятельной оценки.

15.  Зарисовать примеры различных вариантов графиков и выписать характеристики для них из функции «Калькулятор» в пакете STATISTICA.

16. [1, c.12] Изобразите функцию потерь для прибытия в аэропорт позже (или раньше) времени окончания регистрации.

17. [1, c.13] Является ли несмещенность необходимым или достаточным условием состоятельности?

18. Английский тест «ECONTEST» (Режим доступа: C:\APPL\ECONTEST\GO, [9]).

19. В таблице приведены данные об объеме продаж коммерческой фирмы за последние два года. Определите, являлась ли работа фирмы стабильной (проверить гипотезу об однородности выборок).

А) Принять, что объем продаж является нормально распределенной случайной величиной и проверить гипотезу, воспользовавшись параметрическим критерием.

B) Проверить гипотезу о нормальности распределения вероятности объема продаж.

С) В случае невозможности принять гипотезу о нормальности распределения воспользоваться непараметрическими критериями для оценки стабильности работы предприятия.

Месяц	Год 2008	Год 2009
Январь	42	39
Февраль	53	51
Март	51	53
Апрель	64	49
Май	67	62
Июнь	65	66
Июль	50	43
Август	60	59
Сентябрь	55	61
Октябрь	47	52
Ноябрь	51	43
Декабрь	69	67

20. Определить ковариацию потребительского спроса и реальных цен на бензин. Построить диаграмму рассеивания, рассчитать коэффициент корреляции и проверить наличие зависимости между переменными р и y на основе проверки гипотезы о коэффициенте корреляции. Данные в таблице приведены в млрд. долл. в ценах 1972 г.

Год	Цены (р)	Спрос (y)		Год	Цены (р)	Спрос (y)
1973	103,5	26,2		1978	121,6	28,3
1974	127	24,8		1979	149,7	27,4
1975	126	25,6		1980	188,8	25,1
1976	124,8	26,8		1981	193,6	25,2
1977	124,7	27,7		1982	173,9	25,6

21.  Доказать формулу: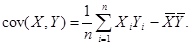

Годовой доход Y гражданина в некоторой стране определяется по следующей формуле:

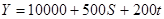
где S – число лет обучения в годах, t – трудовой стаж в годах. Данные о числе лет обучения, трудовом стаже и возрасте 5 индивидов приведены в таблице.

№ п/п	Число лет обучения в годах,  (S)	Трудовой стаж в годах, (t)	Возраст индивида, (X)
1	11	1	18
2	14	6	29
3	12	8	33
4	16	10	35
5	12	5	45

 

 

Рассчитать 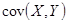, , 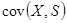 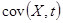по определению и по формуле (см. задачу 13). Получить аналитическое выражение для  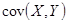и проверить полученное выражение расчетным путем. Построить диаграмму рассеивания, рассчитать коэффициент корреляции и проверить наличие зависимости между переменными X и Y, X и S, X и t на основе проверки гипотезы о коэффициенте корреляции.

23.  Получены данные с1954 по 1965 гг. по приросту численности занятых и темпу прироста выпуска продукции (темпа прироста производительности труда). Эти данные представлены в таблице

№	Страна	Прирост численности занятых, (е)	Темп прироста выпуска продукции, (р)
1	Австрия	2	4,2
2	Бельгия	1,5	3,9
3	Канада	2,3	1,3
4	Дания	2,5	3,2
5	Франция	1,9	3,8
6	Италия	4,4	4,2
7	Япония	5,8	7,8
8	Нидерланды	1,9	4,1
9	Норвегия	0,5	4,4
10	ФРГ	2,7	4,5
11	Великобритания	0,6	2,8
12	США	0,8	2,6

Рассчитать 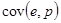 по определению и по формуле (см. задачу 21). Построить диаграмму рассеивания, рассчитать коэффициент корреляции и проверить наличие зависимости между переменными e и p на основе проверки гипотезы о коэффициенте корреляции.

24.  Доказать, что 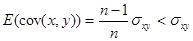(теорема об оценке ковариации).

25.  Дан рынок, состоящий из трех активов a₁, a₂, a₃. Рынок может находиться в одном из трех состояний S₁, S₂, S₃. Данные по вероятностным состояниям и доходностям активов приведены в таблице. Составить ковариационную 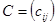,  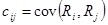и корреляционную 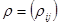,  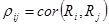матрицы.

Состояния, S	Вероятность, p(S)	Доходность актива, a1 , R1 (%)	Доходность актива, a2 , R2 (%)	Доходность актива, a3 , R3 (%)
S1	0,3	20	30	-10
S2	0,6	20	5	15
S3	0,1	5	-20	15

26.  Проанализировать [10] с точки зрения ТВМС.

27. По семи территориям Уральского регионы за 2005 год получены следующие показатели (см. табл.).

 

 

Район	Расходы на покупку продовольственных товаров в общих расходах в %, Y	Среднемесячная з/п одного работающего в тыс.рублей, X
Удмуртская республика	68,8	4,5
Свердловская область	58,3	5,9
Башкортостан	62,6	5,7
Челябинская область	52,1	7,2
Пермская область	54,5	6,2
Курганская область	57,1	6,0
Оренбургская область	51,0	7,8

Рассчитать параметры следующих функций:

а) линейной;

б) степенной ,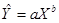

с) показательной .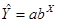

Оценить качество этих регрессий.

28. [1, c.46] По 10 наблюдениям оценена зависимость между инфляцией и безработицей в 1931–1940 гг. Получено: 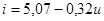, где i – инфляция, u – безработица. Оценена величина стандартной ошибки 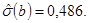Проверить гипотезу H₀:  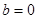при .

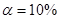29. [1, c.29] Матрица коэффициентов корреляции R является неотрицательно определенной (или положительно полуопределенной), то есть обладает следующим свойством: для любого вектора u скалярное произведение (uR ; u)≥0.

Доказать данное свойство для двумерного и k-мерного случаев.

30. [1, c.33] Покажите, что R ² равен квадрату выборочного коэффициента корреляции 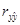между переменными y и .

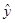31. Используя метод наименьших квадратов, найти коэффициенты уравнения:

а) ;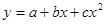

б) .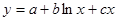

32. Получить решение задачи, разобранной в лабораторной работе №1 [2], в матричном виде для нестандартизированных (т.е. нецентрированных, ненормированных) данных:

.

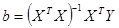33. Составить систему нормальных уравнений для функций:

   1) ,

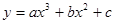   2) .

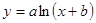34. Зависимость между доходом (доходностью) ценных бумаг и риском следует принципу: чем выше доходность, тем выше риск. Аналитически данное утверждение описывается моделью CAPM ( Capital Asset Price Model ):

,

где r — ожидаемая доходность актива;

r_f — доходность безрисковых активов;

r_m — доходность рынка в среднем;

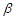— бета-коэффициент, являющийся мерой систематического риска и измеряющий доходность актива по отношению к доходности на рынке в среднем.

Как реализовать задачу линейной регрессии для оценки параметра 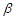 в модели CAMP?

35. Руководство большой шоколадной фабрики заинтересовано в построении модели для того, чтобы предсказать реализацию одной из своих уже долго существующих торговых марок. На основе собранных данных определить «лучшую» модель для прогноза объема реализации.

Дата	Реализация за 6 месяцев млн.ф.ст.	Реклама млн.ф.ст.	Цена, пенсы за ед.	Цена конкурента пенсы за ед.	Индекс потребительских расходов
19X0
I-VI	126	4	15	17	100
VII-XII	137	4,8	14,8	17,3	98,4
19X1
I-VI	148	3,8	15,2	16,8	101,2
VII-XII	191	8,7	15,5	16,2	103,5
19X2
I-VI	274	8,2	15,5	16	104,1
VII-XII	370	9,7	16	18	107
19X3
I-VI	432	14,7	18,1	20,2	107,4
VII-XII	445	18,7	13	15,8	108,5
19X4
I-VI	367	19,8	15,8	18,2	108,3
VII-XII	367	10,6	16,9	16,8	109,2
19X5
I-VI	321	8,6	16,3	17	110,1
VII-XII	307	6,5	16,1	18,3	110,7
19X6
I-VI	331	12,6	15,4	16,4	110,3
VII-XII	345	6,5	15,7	16,2	111,8
19X7
I-VI	364	5,8	16	17,7	112,3
VII-XII	384	5,7	15,1	16,2	112,9

36. По данным за 7 месяцев построено уравнение регрессии зависимости прибыли предприятия y (млн. руб.) от объема реализации 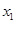(тыс. руб. за 1 т) и производительности труда 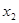(ед. продукции на 1 работника):

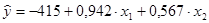
при анализе остаточных величин были использованы значения, приведенные в табл.

№	y	x 1	x 2
1	700	900	300
2	1200	1200	700
3	850	1180	400
4	920	1050	600
5	680	960	550
6	800	1100	350
7	700	950	650

требуется:

1) по семи позициям рассчитать

2) рассчитать критерии Дарбина - Уотсона.

3) Оценить полученный результат при 5%-ном уровне значимости.

4) Указать, пригодно ли уравнение для прогноза.

37. y зависит от x как квадратичная функция вида:

1. ;

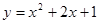2. .

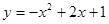Если оценена связывающая их линейная регрессия, то какой (примерно) можно ожидать величину DW?

38. «Большое домашнее задание» (БДЗ) - выполнение двух лабораторных работ по собственным исходным данным.

3 9 . Реферат.

Задание для реферата.

Содержание реферата должно отражать следующие темы:

1. Метод наименьших квадратов (МНК):

а) трехшаговый МНК;

б) косвенный МНК;

в) обобщенный МНК.

2. Линейные регрессионные модели с гетероскедастичными и автокорреляционными остатками.

3. Регрессионные модели с переменной структурой (фиктивные переменные).

Каждый пункт из перечисленных выше не должен превышать объем 1 страницы и должен включать следующую информацию:

1. В чем смысл использования (для каждого вида МНК – отличие от обычного МНК).

2. Схема применения.

3. Пример.

Дополнительное задание для реферата:

1. Придумать 2-3 вопроса с выбором вариантов ответа (4-5 вариантов для каждого вопроса).

2. Придумать задачу (дать с решением).

В конце реферата дать список литературы с указанием ссылок по тексту реферата.

 

40. Написать спецификацию моделей, если следующие записи имеют смысл:

  1) DL(3), DL(2,1)

  2) AR(4), AR(1,0)

  3) ADL(1), ADL(3,2)

  4) ARMA(2,1), ARMA(0,1)

  5) ARIMA(2,3), ARIMA(2,2,1)

41. Составить систему нормальных уравнений для функций:

   1) ;

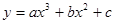   2) .

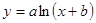42. Убедиться, что запись 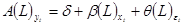 является компактной универсальной записью различных моделей.

Указание. Подставить выражения для полиномов оператора.

43. Используя метод наименьших квадратов (МНК), построить уравнение регрессии с компонентом AR в виде 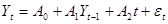 для прогнозирования объема реализации на основе следующих данных о динамике этого показателя (млн. руб.): 17, 16, 21, 24, 23, 26, 28. Можно ли использовать построенное уравнение для прогнозирования?

Указание.

1.Промежуточные данные для удобства оформите в виде таблицы:

Yt-1	t	Yt	Y2t-1	t2	tYt-1	tYt	YtYt-1	Прогнозное значение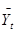
ИТОГО:

2. Уравнение можно использовать для прогнозирования при выполнении следующего условия:

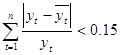 (15%).

44. Показать, что «белый шум» 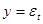, где 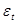~  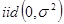является стационарным процессом.

45. Стационарен ли ряд 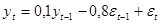 и почему?

 Рассматривать исходя из двух условий:

1. условия устойчивости ряда;

2. условия слабой стационарности.

46. Дан ряд с линейным трендом вида 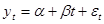,где 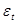~ 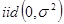. Показать, что взятие разности первого порядка приводит этот ряд к стационарному.

47. Найти чему равно: а) Δ²y_t , б) Δ³y_t.

48. Дан ряд вида 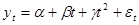, где 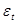~ 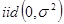. Приводит ли взятие разности:

а) первого порядка ряд к стационарному?

б) второго порядка ряд к стационарному?

49. Показать, что для ряда вида: 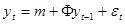, где 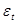~ 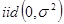, выполняется:

.

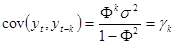50. Истинно, ложно или не определено следующее утверждение: «Любая эконометрическая модель является по сути динамической»? Ответ пояснить.

51. Истинно, ложно или не определено следующее утверждение: «В авторегрессионной модели в лаговой форме используется лишь зависимая переменная»? Ответ пояснить.

52. Истинно, ложно или не определено следующее утверждение: «С увеличением величины лага влияние объясняющей переменной на зависимую падает, что отражается на статистической значимости соответствующего коэффициента регрессии»? Ответ пояснить.

53. Истинно, ложно или не определено следующее утверждение: «В модели с распределенными лагами добавление новых лагов осуществляется до тех пор, пока соответствующие t-статистики указывают на статистическую значимость коэффициентов»? Ответ пояснить.

54.  Получить полином оператора сдвига 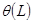 для следующей спецификации MA ( q ):

.

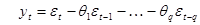Имеет ли значение знак перед коэффициентом 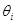  в спецификации MA(q) и почему?

Литература

1. Левин М.И., Пахомова Е.А. Эконометрика: Учебное пособие. – Дубна: Международный университет природы, общества и человека «Дубна», 2000. – 71с.

2. Левин М.И., Пахомова Е.А., Васильева Н.В. Эконометрика: Практикум. – Дубна: Международный университет природы, общества и человека «Дубна», 2000. – 44с.

3. Бородич С.А. Эконометрика: Учеб. пособие / Мн.: Новое знание, 2001. – 408с.

4. Магнус Л.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учеб. – 3–е изд., перераб. и доп. М: Дело, 2000.– 400с.

5. Практикум по эконометрике: Учеб. пособие / Под ред. И.И. Елисеевой.– М.: Финансы и статистика, 2001. – 192с.

6. Домбровский В.В. Эконометрика: Учебник. – М.: Новый учебник, 2004. – 344с.

7. Электронный курс «Эконометрика» в СДО

8. Электронный курс «Эконометрика. Практикум» в СДО

9. Пароли для выполнения английского теста «ECONTEST» (Приложение 1)

10. Kendall M.G. Hiahawatha designs an experiment [11, с.22] (Приложение 2)

11. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1997 - XIV, 402 с.

 

Приложение 1.

Приложение 2.

M.G. Ке ndall

---

Дата добавления: 2021-03-18; просмотров: 167; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!