Тестовая задача на инструментарий гипотез
Учебный план по дисциплине «Эконометрика»
| № п/п | ТЕМА | ЗАДАЧИ | ||
| 1 | Контрольная работа по проверке остаточных знаний по ТВ и МС. | § Т1*, Т2, Т3 | ||
| 2 | Проверка гипотез на основе выборочной средней при известной генеральной дисперсии. | § 2.1**, 2.2, 2.3, 2.4; § Т4, Т5, Т6, Т7 (задача про рассаду); § Решение задач и выполнение тестов в СДО «Эконометрика» и «Эконометрика. Практикум» по указанной теме. | ||
| 3 | Проверка гипотез на основе выборочной средней при неизвестной генеральной дисперсии. | § 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7; § Т8, Т9, Т10; § Решение задач и выполнение тестов в СДО «Эконометрика» и «Эконометрика. Практикум» по указанной теме. | ||
| 4 | Проверка гипотезы о двух генеральных дисперсиях.. | § 4.1, 4.2; § Т11, Т12; § Решение задач и выполнение тестов в СДО «Эконометрика» и «Эконометрика. Практикум» по указанной теме. | ||
| 5 | Сравнение средних величин двух выборок. Решение задач с помощью пакета STATISTICA. | § 5.1, 5.2, 5.3, 5.4, 5.5 (задача про контролеров); § T13, Т14, Т15, Т16, Т17, Т18, Т19; § Решение задач и выполнение тестов в СДО «Эконометрика» и «Эконометрика. Практикум» по указанной теме. | ||
| 6 | Ковариация. Корреляция. Диаграмма рассеивания. Проверка гипотез о коэффициенте корреляции. | T20, T21, T22, T23, Т24, Т25, Т26 | ||
| 7 | Парная регрессия. Построение линейной, степенной и показательной регрессий. Оценка и анализ регрессии. | § Т27, Т28; § Лабораторная работа №1 (пункт 5)**, задача 1 после лабораторной работы №1 (стр.32)** | ||
| 8
| Множественная линейная регрессия. Вычисление коэффициентов уравнения линейной регрессии для: а) стандартизированных данных в матричном виде; б) нестандартизированных данных. | § Лабораторная работа №1; § Т29, Т30, Т31, Т32, Т33, Т34 | ||
| 9 | Построение наилучшей модели линейной регрессии. | § Т35 | ||
| 10 | Предпосылки МНК. Критерий Дарбина-Уотсона. | § Т36, Т37 | ||
| 1 11 | Системы линейных структурных уравнений | § Лабораторная работа №2; § Большое домашнее задание (Т38) | ||
| 12 | Разновидности МНК: трехшаговый, косвенный обобщенный. Линейные регрессионные модели с гетероскедастичными и автокорелляционными остатками. Регрессионные модели с переменной структурой (фиктивные переменные) | § Т39 | ||
| 13 | Временные ряды. | § Т40 – Т54 | ||
| 14 | Вопросы Интернет-экзамена. | § Файлы «Тестирование по эконометрике_2009», тестир_декабрь_2011.doc (см. студенческий компьютер, папка преподавателя, директория «Эконометрика») | ||
| 15 | Сдача БДЗ и реферата. |
*Примечание. Текстовые задачи (условия см. ниже).
**Примечание. Номера задач указаны по сборнику «Эконометрика. Практикум» Н.В.Васильева, М.И.Левин, Е.А.Пахомова (первая цифра – номер соответствующей темы; вторая – номер задачи).
|
|
|
Тестовые задачи
Контрольная работа №1 (проверка остаточных знаний)
ВАРИАНТ 1
1. Даны цены продаж домов в Hickville $80000, $90000, $100000, $150000, $150000. Найти модальную цену и стандартное отклонение цен.
2. Дана таблица распределения возрастов и их соответствующих частот детей, посещающих начальную школу АВС.
| Возраст | 3 | 4 | 5 |
| Частота | 10 | 18 | 27 |
Найти средний возраст детей и процент детей не старше 4 лет. Чему равна дисперсия выборки?
3. Компания А имеет 3 уровня заработной платы и 13 служащих. Данные по количеству служащих и их зарплате приведены в таблице:
| Уровень | Зарплата | Количество служащих |
| 1 | $1800 | 4 |
| 2 | $1900 | 7 |
| 3 | $2000 | 2 |
Найти относительные частоты. Как изменятся среднее месячное жалованье служащего и дисперсия выборки, если один служащий перейдет со второго уровня жалования на третий?
ВАРИАНТ 2
1. Продажа бытовой техники в магазине Дункана с 8.00 до 9.00 утра составляет: $0.98, $0.98, $11.50, $20.01, $16.02 . Найти среднее значение продажи бытовой техники и дисперсию сбыта в магазине.
2. Дана таблица распределения возрастов и их соответствующих частот студентов музыкального класса школы АВС.
| Возраст | 13 | 14 | 15 |
| Частота | 22 | 28 | 36 |
Найти средний возраст студентов и процент студентов старше 14 лет. Чему равно стандартное отклонение выборки?
|
|
|
3. Компания В имеет 3 уровня заработной платы и 16 служащих. Данные по количеству служащих и их зарплате приведены в таблице:
| Уровень | Зарплата | Количество служащих |
| 1 | $1400 | 5 |
| 2 | $1600 | 8 |
| 3 | $2100 | 3 |
Найти относительные частоты. Как изменятся среднее месячное жалованье служащего и дисперсия выборки, если двое служащих с первого уровня будут уволены?
Некоторые теоретические сведения для решения контрольной работы №1
Мода - наиболее часто встречающееся значение случайной величины в выборке.
Случайная величина – это переменная, которая под воздействием случайных факторов может с определенными вероятностями принимать те или иные значения из некоторого множества чисел. Случайной величине нельзя приписать определенное значение (даже при фиксированных обстоятельствах), но можно приписать несколько значений, которые она принимает с определенными вероятностями.
Расчет математического ожидания для дискретной случайной величины сводится к нахождению выборочного среднего:
, (1)
где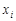 
, 
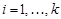— значения случайной величины x ,
|
|
|
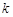— количество различных значений 
случайной величины x,
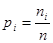— вероятность принять случайной величине 
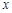значение 
,
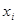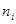— количество «благоприятных» исходов (то есть частота принятия случайной величиной x значения ), 
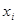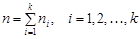— общее число исходов.
Для наглядности указанные характеристики случайной величины x представим таблицей:
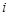
| xi |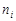 
|
| 1 |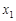 
| 
|
|
|
|
|
| 
| 
|
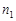
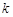
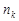
Для дисперсии по определению имеем:
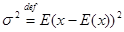, (2)
где def — означает by definition, «по определению».
После преобразований выражения (2) имеем:
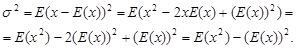(3)
В случае дискретной случайной величины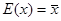 
и выражения (2) — (3) примут вид:
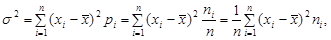(4)
(5)
Результат (5) читается так: «Дисперсия = средний квадрат – квадрат среднего».
Тестовая задача на инструментарий гипотез
Рассматривается месячный доход жителей России.
a) Пусть месячный доход жителей России распределен по нормальному закону со средним 1000 руб. и дисперсией 10000 руб2. Найти вероятность того, что душевой доход лежит между 800 и 1200 руб.
b) При выборочном опросе 1000 человек оказалось, что выборочное среднее составило 900 руб., а оценка выборочной дисперсии 9000 руб2. Постройте 95 % доверительный интервал для генерального среднего.
c) Пусть месячный доход жителей России распределен по нормальному закону со средним 1000 руб., а значение дисперсии генеральной совокупности неизвестно. При выборочном опросе 1000 человек оказалось, что оценка выборочной дисперсии 9000 руб2. Данные о выборочном среднем случайно оказались утеряны. На уровне 10 % значимости проверьте гипотезу о том, что генеральное среднее[1] равно 950 руб.
3. Какие основные понятия из курса «Эконометрика» могут быть включены в следующее изречение: «Ex ungue leonem. A l’ongle on connait le lion (en francais). По когтю льва (узнают)»?
4. [1, c.9] a) Доказать следующие свойства математического ожидания:
E(a),
.
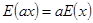b) Пусть случайная величина x имеет математическое ожидание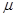 
и дисперсию 
. Показать, что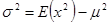 
.
5. [1, c.27] Показать, что для случайной величины z, определенной по формуле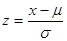 
,
где x – нормально распределенная случайная величина, 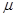– математическое ожидание случайной величины x, 
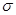– стандартное отклонение, выполняются следующие соотношения:
, 
, 
.
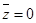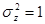6. [1, c.39]Найти абсциссы точек пересечения графиков функций плотности вероятности нормального распределения, имеющих математическое ожидание 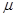, дисперси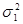и 
и 
соответственно (рис. 4.4 «Эконометрика. Учебное пособие»).
7. Высота отдельных ростков рассады распределена нормально со средней, равной 53 см, и дисперсией 12 см2. В прошлом году в ящик, в котором были высажены 15 таких растений, была внесена по ошибке двойная норма удобрений. Средняя высота рассады в этом ящике достигла 55 см. Есть ли какое-либо основание полагать, что внесение повышенного количества удобрений дало положительный эффект?
8. [1, c.41] Пусть x – нормально распределенная случайная величина; 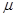– математическое ожидание случайной величины x; 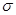– стандартное отклонение; 
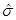– несмещенная оценка стандартного отклонения; x 1 ,…, xn – выборка объема n.
Показать, что величина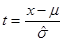 
распределена по Стъюденту с 
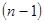степенями свободы.
9. [1, c.54] Имеется выборка из 60 наблюдений по индексу доходности. При этом выборочное среднее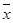 
= 1,125 %, стандартное отклонение S = 2,5 %. Каким будет 95 % доверительный интервал?
10. Для предприятий, торгующих продуктами питания, установлены показатели эффективности деятельности: уровень рентабельности товарооборота – 20% и средняя оборачиваемость запасов – 12 дней. Более низкие показатели эффективности означают снижение конкурентоспособности предприятия. В целях оперативного контроля результатов коммерческой деятельности в одной из торговых фирм проведен анализ эффективности торговых операций за последние 10 месяцев и получены данные (см. таблицу). Используя эти данные, определите, является ли эффективность коммерческой деятельности фирмы удовлетворительной, т.е. соответствуют ли полученные показатели эффективности нормативным.
| Месяц | Рентабельность, % | Продолжительность товарооборота, дни | |
| 1 | 14 | 19 | |
| 2 | 12 | 15 | |
| 3 | 16 | 19 | |
| 4 | 14 | 1 | |
| 5 | 15 | 24 | |
| 6 | 18 | 12 | |
| 7 | 22 | 10 | |
| 8 | 20 | 15 | |
| 9 | 13 | 18 | |
| 10 | 9 | 20 |
11. [1, c.11] Имеются две оценки неизвестного параметра генеральной совокупности. Обязательно ли является более эффективной та из них, которая имеет меньшую дисперсию?
12. [1, c.43] Показать, что F-критерий, используемый для сравнения двух дисперсий, подчиняется распределению Фишера.
Дата добавления: 2021-03-18; просмотров: 151; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!