Математична модель руху часток у потоці.
Рух твердих часток в потоці на ділянці повороту русла
Шиф р “Приховані закономірності”
Зміст
Ст.
Вступ……………………………………………………………………………….3
1. Початок руху твердих часток, які лежать на дні…………………………..4
2. Математична модель руху часток у потоці……………………………….11
3. Поздовжні та поперечні швидкості течії на повороті турбулентного потоку для випадку гладкого дна………………………………………….13
4. Розв’язання системи рівнянь, за якою обчислюється рух твердої частки в турбулентному потоці……………………………………………………...23
5. Розрахунок руху твердих часток в циркуляційному потоці……………..25
Висновок………………………………………………………………………….28
Список використаної літератури………………………………………………..29
Вступ
Об’єктом дослідження є двохфазний турбулентний потік в штучних і природних криволінійних руслах.
Предметом дослідження є швидкості осереднених поздовжніх і циркуляційних течій в криволінійному руслі, а також траєкторії твердих часточок які переносяться потоком.
Актуальність теми витікає із того, що існує багато практичних задач, пов’язаних з необхідністю розрахунку руху часток у двохфазовому турбулентному потоці, зокрема, в криволінійних штучних і природних руслах. Відомо, що ефективність водозабірних споруд, які проектуються на річках та каналах гірсько-передгірської зони, в значній мірі залежить від кількості наносів, які потрапляють у водоприймач. Для зменшення цієї кількості широко використовуються гідротехнічні методи, пов’язані зі збудженням циркуляційних течій в потоці. Саме такі течії є ефективними з точки зору організації транспорту наносів в необхідному напрямку. Транспортування наносів ними пов’язане з підвищеною наносотранспортуючою здатністю течії, в яких є циркуляція. В минулому було запропоновано цілий ряд цікавих конструкцій, які реалізують даний принцип при водозаборі, але, нажаль, методики гідротехнічного розрахунку такого роду конструкцій не існує. На сьогодні відкривається широка перспектива будівництва малих ГЕС, невеликих гідровузлів в гірських та передгірських районах, тому дослідження наносотранспортуючої спроможності таких потоків є актуальними.
|
|
|
Наукова новизна. Вданій роботі вперше робиться аналіз умов роботи твердих часток в криволінійному циркуляційному потоці. Вперше також розроблений алгоритм для розрахунку траєкторій таких часток.
|
|
|
Початок руху твердих часток, які лежать на дні
Розглянемо моделі відриву і перенесення в потоці окремих часток неоднорідного незв’язного ґрунту, які можуть дати картину переформування дна перед спорудами у відносно однорідних і дрібних ґрунтах, а також дати можливість оцінити ефективність засобів регулювання руху наносів при водозаборі. Для оцінки ймовірності відриву від дна і винесення потоком окремих часток незв’язного неоднорідного ґрунту застосуємо метод імітаційного моделювання.
Основними факторами, що визначають умови відриву окремої частинки від дна, є діючі на неї зовнішні навантаження, а також сили інерції, пов’язані з прискоренням частинки в початковий момент її руху. В якості зовнішніх навантажень розглядаються сили власної ваги, Архімедові сила, а також гідродинамічна сила взаємодії турбулентного потоку з нерухомою частинкою.
Зовнішні гідродинамічні сили, що діють на будь-яку частинку, яка лежить на поверхні, визначаються умовами обтікання цієї частинки, тобто кінематичними і динамічними характеристиками потоку поблизу дна. Зміни ж миттєвих швидкостей і тиску в придонній області потоку носять випадковий, стохастичний характер і можуть бути представлені детерміністичними характеристиками - значеннями моментів розподілу, автокореляційною функцією та спектральною густиною випадкового процесу. Неоднорідність механічного складу наносів, параметри їх форми і укладка також задаються статистично.
|
|
|
В роботах багатьох авторів, наприклад, М. А. Дементьєва, І. І. Леві, В. С. Кнороза, Ц. Є. Мірцхулави та ін. проводиться детальний аналіз механізму взаємодії потоку з донними частинками, викривається природа сил, що впливають на відрив частинок і приводяться кількісні залежності, що дозволяють ці сили визначити. Проте в роботі всіх авторів не враховані реальні ймовірні закони зміни факторів, що визначають взаємодію потоку з донними частинками і відрив самих частинок від дна. В роботах К.В. Гришаніна, В.М. Доненберга, В.О. Базилевича та інших вчених обґрунтовано статистичний підхід до проблеми відриву і початку руху донних частинок. Показано, що ймовірність відриву частинок пов’язана статистичними закономірностями зміни поздовжньої швидкості або дотичної напруги на дні.
У всіх роботах розглядаються не всі можливі види втрат стійкості частинки, а тільки викочування її із гнізда, або вертикальний підйом, розв’язуються відповідні рівняння руху цієї частинки.
|
|
|
Автори ряду робіт враховують стохастичні властивості турбулентного потоку, але не розглядають процесу руху самої частинки з врахуванням її інертності. Їх припущення про рівність між кількістю змивів частинок і перевищення миттєвих швидкостей потоку критичних значень виконується лише наближено і точніше для відносно дрібних часток.
При проведенні досліджень в роботі прийнята статистична модель відриву твердих часток від дна, виконані числові розрахунки по визначенню ймовірності відриву окремих часток, що лежать на по верхні дна. При цьому розв’язувалась задача статистичної імітації зовнішніх впливів, а також інтегрувались рівняння руху частинок від початку їх руху до моменту відриву від дна.
Особливості розв’язку задачі :
1) Розглядається велика група окремих придонних частинок кулеподібної форми різних діаметрів, розподілених у відповідності із заданою кривою гранулометричного складу донних відкладень.
2) Для кожного розрахунку приймається частка з діаметром, знайденим з допомогою генератора випадкових чисел з тим самим розподілом і середніми характеристиками, що й параметри натурної суміші.
3) Розрахунок повторюється для часток різних діаметрів мінімум 100 разів і, таким чином, враховується неоднорідність складу ґрунту.
4) Імітація вертикальних, горизонтальних і дотичних сил, що діють на частинку, проводиться у відповідності з даними попередньої статистичної обробки миттєвих швидкостей та тисків у придонній області воронки розмиву, знайдених на фізичній моделі споруди у лабораторії. Причому імітуються випадкові числа, що мають ті ж середні значення, дисперсію і автокореляційні функції, що й задана послідовність випадкових чисел.
5) Ймовірність викиду визначається шляхом розв’язку повної системи диференціальних рівнянь, що описують початкову стадію їх руху. При цьому частинка вважається відірваною від дна, якщо час відриву менший або дорівнює часу впливу.
|
|
Рис.1. Схема сил, які діють на частку в потоці
На рис.1 представлена схема силових впливів на одиноку кулеподібну частинку, що лежить на поверхні дна та обтікається потоком. Нормальні і дотичні сили, що діють на частинку, розподілені нерівномірно.. Горизонтальну і вертикальну складові сили Р позначимо Рх та Рy.
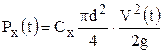 ;
;  ; (1)
; (1)
Для системи координат, позначеній на рис.1, запишемо рівняння динамічної рівноваги частинок з врахуванням сил інерції, що включаються до принципу Д’Аламбера в систему зрівноважених сил:
 ; (2)
; (2) 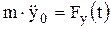 ; (3)
; (3)
 ;
; 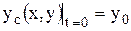 ; (4)
; (4)
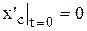 ;
; 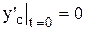 ; (5)
; (5)
 ; (6)
; (6)
 ;
;  ; (7)
; (7)
Тут хс, ус - координати центру мас частинки;
m - маса частинки з врахуванням приєднаної маси води;
х0, у0, - координати центру в момент часу t =0;
Fx та Fy - проекції рівнодіючої всіх діючих сил на осі ОХ та ОY відповідно;
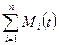 - сума моментів, що діють на частинку;
- сума моментів, що діють на частинку;
I - момент інерції кулеподібної частинки відносно осі, що проходить через точку дотику О.
Рівняння характеризує обертовий рух частинки навколо осі О.
Розпишемо праві частини рівнянь (2) та (3).
Fx(t) = Rx(t) - Px(t) - T(t) (8);
Fy(t) = Ry(t) + Py(t) + Fapx - G (9),
Fapx – сила Архімеда;
R - радіус частки;
Т – розрахунковий період часу;
G – власна вага частинки.
Розглядається три можливих варіанти відриву частки від дна. Перший - вертикальний відрив - має місце, коли сума вертикальних підйомних сил, що діють на частинку, стає більшою суми сил ваги і вертикальної складової сили тертя Fy(t) >= 0. Другий - обертання частки навколо точки О та її відрив від точки дотику в момент, коли реакція опори R(t) <= 0 стає рівною нулю. Третій варіант - перекочування частки ґрунту через сусідню частку і подальший її рух у формі перекочування. При цьому частка повністю залишає своє гніздо, коли її кут повороту стає більшим p/2.
 ; (10)
; (10)
 ; (11)
; (11)
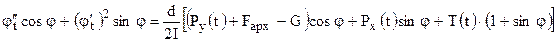 ; (12)
; (12)
 ;
; 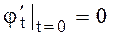 ; (13)
; (13)
де d - діаметр часток.
Алгоритм статистичної імітації працює наступним чином. Генерується випадковий діаметр частки і розв’язується рівняння початкового руху частки при багатьох випадкових значеннях швидкостей потоку. Основні сили, що діють на частинку, визначаються по формулах :
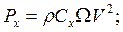
 (14)
(14)
де Сх та Cy - коефіцієнти опору частки (знаходяться за даними вимірювань А.В.Мацеї);
W - площа міделевого перетину частки.
Потім розв’язується система диференціальних рівнянь (2-3) та визначається функція j(t) , а також складові реакції в точці опори. Після чого перевіряються умови відриву. Якщо одна з умов виконується, фіксується факт відриву частки. Після випробування першої частки генерується наступний діаметр і розрахунок повторюється. Після завершення циклу визначається ймовірність відриву часток P = n / N, де n та N - число часток, що відірвались, та загальне їх число.
Результати розрахунків дозволяють оцінити також нерозмиваючу швидкість потоку із заданою надійністю. Для умов рівномірної течії збіжність даних розрахунків з даними вимірів Ц.Є. Мірцхулави характеризується коефіцієнтом якості апроксимації 0.943, що вказує на задовільну збіжність, бо граничне допустиме значення становить 0.8 - 0.85.
Результати дослідження критичних швидкостей при заданому рівні турбулентності в потоці наведено в таблиці 1.
Таблиця 1
Значення критичних швидкостей викочування або відриву кулеподібних частинок при h уст / D = 1/3 і синусоїдальному характеру зміни придонної швидкості частинки 
| D , м | Vo , м/с при Ksg, р івному | ||
| 0,1 | 0,2 | 0,3 | |
| 0,0002 | 0,078 | 0,064 | 0,056 |
| 0,001 | 0,176 | 0,147 | 0,126 |
| 0,002 | 0,249 | 0,208 | 0,178 |
| 0,0025 | 0,279 | 0,232 | 0,201 |
| 0,005 | 0,399 | 0,335 | 0,289 |
| 0,01 | 0,571 | 0,485 | 0,42 |
| 0,03 | 1,05 | 0,876 | 0,767 |
| 0,05 | 1,343 | 1,16 | 1,02 |
| 0,075 | 1,656 | 1,453 | 1,281 |
| 0,1 | 1,932 | 1,704 | 1,507 |
| 0,125 | 2,177 | 1,928 | 1,708 |
| 0,15 | 2,4 | 2,132 | 1,891 |
| 0,2 | 2,797 | 2,496 | 2,218 |
Математична модель руху часток у потоці.
Для обрахунку траєкторії руху часточки достатньо розв’язати систему трьох(по осях X, Y, Z) рівнянь, які є наслідком другого закону Ньютона:

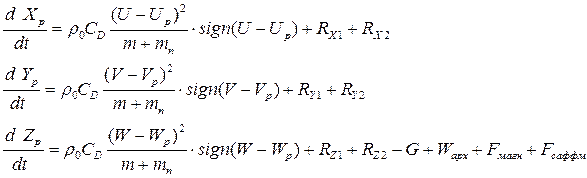 (15)
(15)
де U,V,W – швидкості по осях X,Y,Z (генеруються генератором) ;
СD – коефіцієнт обтікання;
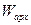 - Архімедова виштовхувальна сила;
- Архімедова виштовхувальна сила;
 - сила Магнуса;
- сила Магнуса;
 - сила Саффмена.
- сила Саффмена.
Для розв’язку зазначеної системи нами проводиться зниження її порядку. Переходячи від невідомих координат частки до їх швидкостей ми знижуємо порядок системи на одиницю. Ця система виглядає наступним чином

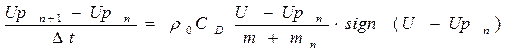
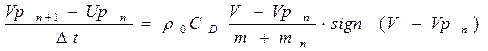

(16)
Внаслідок зменшення порядку системи появляється необхідність інтегрувати ще одну систему, яка складається з трьох наступних диференціальних рівнянь першого порядку.
 (17)
(17)
Зазначенні диференціальні рівняння інтегруються при наступних початкових умовах: при визначенні швидкостей часток, початковими умовами будуть:
 ,
,
при визначенні координат часток:

Дата добавления: 2021-03-18; просмотров: 74; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

