Кинетическая энергия и работа
Модуль 1.3
ГЛАВА 3 Механическая энергия и работа. Закон сохранения энергии
Работа и мощность
Пусть частица под действием силы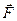 
совершает перемещение по некоторой траектории 1-2 (рис.3.1).
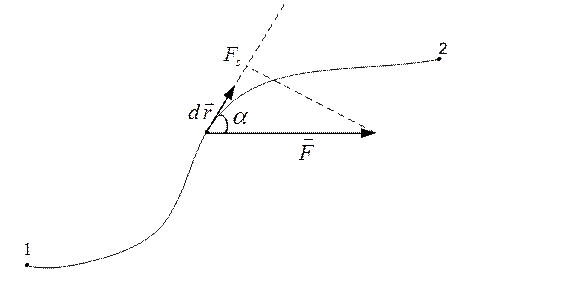
Рис. 3.1
Элементарной работой силы на перемещении 
называется скалярное произведение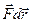 
.
Итак,
(3.1)
где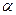 
- угол между векторам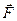и и ,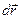 
- элементарный путь, 
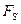- проекция вектора 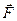на вектор .
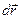Суммируя (интегрируя) выражение (3.1) на участке от точки 1 до точки 2, находим работу силы 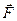на данном пути:
. (3.2)
В выражении (3.2) под 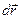(или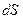 
) следует понимать перемещение точки приложения силы .
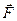Рассмотрим несколько примеров на вычисление работы
1. Работа упругой силы
Работа упругой силы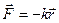 
, где 
- радиус-вектор частицы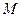 
относительно точки 
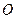(рис.3.2).
Элементарная работа
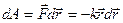
Рис. 3.2
Скалярное произведение
и 
.
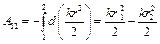. (3.3)
2. Работа гравитационной (или кулоновской) силы
Пусть в точке 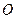(рис.3.3) находится неподвижный силовой центр – материальная точка, действующая на частицу 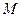с силой 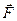, которая как для гравитационного, так и для кулоновского взаимодействий может быть представлена в виде:
|
|
|
,
где 
для гравитационной силы,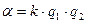 
для кулоновской силы, 
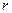- расстояние от точки 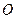до частицы , 
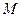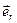- орт радиус-вектора .
Рис. 3.3
Элементарная работа этой силы на перемещении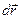
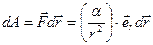, где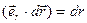 
,
поэтому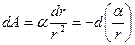 
.
Работа этой силы на всем пути от точки 1 до точки 2
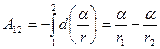. (3.4)
3. Работа однородной силы тяжести
Запишем эту силу в виде 
, где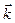 
- орт вертикальной оси 
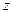(рис. 3.4).
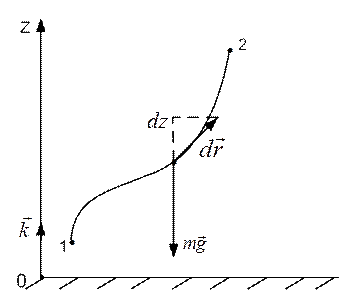
Рис. 3.4
Элементарная работа силы тяжести на перемещении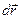
.
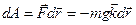Скалярное произведение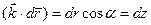 
, поэтому
.
Работа данной силы на всем пути от точки 1 до точки 2
.
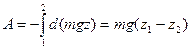Полагая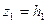 
, 
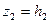, получим
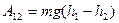. (3.5)
Вывод: рассмотренные силы интересны в том отношении, что их работа, как видно из (3.3) – (3.5), не зависит от формы пути между точками 1 и 2, а зависит только от положения этих точек. Таким свойством обладают не все силы. Например, сила трения этим свойством не обладает: работа этой силы зависит не только от положения начальной и конечной точек, но и от формы пути между ними.
Единицей измерения работы в СИ является джоуль (Дж).
|
|
|
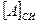= 1 Дж = 1 Н·м.
Мощность
Работа, совершаемая в единицу времени, называется мощностью. Мощность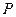 
определяется соотношением
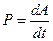. (3.6)
Учитывая, что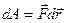 
, 
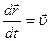, получим
. (3.7)
Таким образом, мощность равна скалярному произведению силы на скорость точки приложения силы.
Единицей мощности в СИ является ватт (Вт).
.
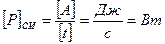Консервативные силы. Потенциальная энергия
Консервативные силы
Если в каждой точке пространства на помещенную туда частицу действует сила, то частица находится в поле сил. Так, например, частица может находиться в поле сил тяжести, в поле сил сопротивления.
Поле, остающееся постоянным во времени, называют стационарным. В стационарном силовом поле сила, действующая на частицу, зависит только от ее положения.
Силы, работа которых не зависит от пути, по которому двигалась частица, а зависит лишь от начального и конечного положений частицы, называют консервативными (или потенциальными).
Работа консервативных сил на любом замкнутом пути равна нулю. Примером являются силы гравитационные, кулоновские, упругие, сила тяжести.
|
|
|
К числу неконсервативных сил относятся, например, силы трения и сопротивления. Работа этих сил зависит, вообще говоря, от пути между начальным и конечным положениями частицы (и не равна нулю на любом замкнутом пути).
Поле, в любой точке которого направление силы, действующей на частицу, проходит через неподвижный центр, а модуль силы зависит только от расстояния 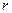до этого центра, называется центральным. Направлена сила либо от центра (как на рис. 5), либо к силовому центру.
Центральную силу можно представить в виде:
. (3.8)
Найдем работу, совершаемую над частицей в центральном стационарном силовом поле.
Элементарная работа силы (3.8) на перемещении 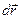есть
, 
,
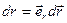- проекция вектора 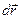на вектор .
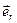Работа этой силы на всем пути от точки 1 до точки 2
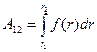. (3.9)
Рис. 3.5
Это выражение зависит только от вида функции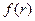 
и от значени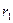й 
и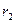 
- начального и конечного положения частицы. От формы траектории оно никак не зависит.
|
|
|
Вывод: силы центрального стационарного поля являются консервативными.
Потенциальная энергия частицы в поле
То обстоятельство, что работа консервативных сил в случае стационарного поля зависит только от начального и конечного положения частицы, дает возможность ввести понятие потенциальной энергии. Сопоставим каждой точке поля значение некоторой функции координат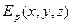 
.
Работа сил поля при перемещении частицы из точки 1 в точку 2 будет равна разности значений 
и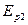 
, которые величина 
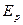принимает в точках 1 и 2:
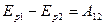. (3.10)
Величина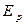 
называется потенциальной энергией частицы в силовом поле.
Таким образом, работа консервативных сил совершается за счет убыли потенциальной энергии частицы в данном поле.
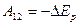. (3.11)
Равенство (3.10) определяет лишь разность потенциальных энергий в двух точках, саму потенциальную энергию можно определить, если условно принять за нуль значение потенциальной энергии в какой-либо точке пространства.
В предыдущем параграфе мы нашли, что работа силы упругости равна
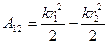
(см. 3.3). С другой стороны, по формуле (3.10)
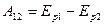
Отсюда потенциальная энергия частицы в поле упругой силы
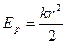(3.12)
Сопоставление формул (3.4) и (3.10) дает, что потенциальная энергия частицы в гравитационном поле:
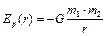, (3.13)
в кулоновском поле:
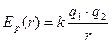. (3.14)
Из формул (3.5) и (3.10) следует, что потенциальная энергия частицы в однородном поле сил тяжести
, (3.15)
где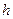 
отсчитывается от произвольного уровня.
Связь между потенциальной энергией 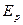и силой поля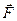
Если известно выражение 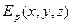для потенциальной энергии, можно найти силу, действующую на частицу в каждой точке поля. Пусть частица совершила перемещение 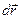под действием силы 
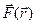, тогда работа этой силы равна
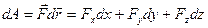. (3.16)
С другой стороны, согласно формуле (3.11) эта работа равна убыли потенциальной энергии:
. (3.17)
Полный дифференциал 
можно представить в виде:
, (3.18)
где символ частной производной, например, 
означает, что производная по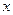 
вычисляется при условии, что координаты 
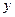и 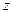остаются постоянными.
Подставляя (3.16) и (3.18) в (3.17), получим
,
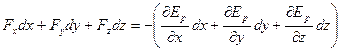отсюда компоненты силы равны
; 
; 
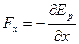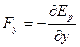. (3.19)
Вектор силы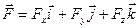 
или
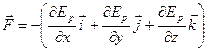. (3.20)
Величину, стоящую в скобках, называют градиентом скалярной функции 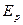и обозначают 
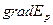или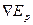 
, где оператор
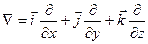(3.21)
называется оператором Гамильтона или оператором набла.
Таким образом,
, или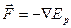 
, (3.22)
т.е. консервативная сила равна градиенту потенциальной энергии частицы в данной точке поля, взятому со знаком минус.
Кинетическая энергия и работа
Пусть частица массы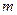 
движется под действием некоторой силы 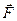(в общем случае сила 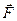может быть результирующей нескольких сил). Найдем элементарную работу, которую совершает эта сила 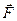на перемещении 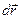. Имея в виду, что
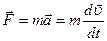и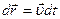 
,
запишем
.
Скалярное произведение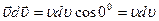 
, поэтому
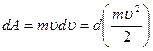. (3.23)
Отсюда видно, что работа результирующей силы 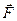идет на приращение некоторой величины, которую называют кинетической энергией:
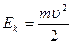. (3.24)
Проинтегрируем обе части равенства (3.23) вдоль траектории частицы от точки 1 до точки 2:
.
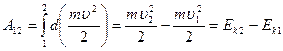Таким образом, мы пришли к соотношению
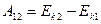, (3.25)
из которого следует, что работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы.
Дата добавления: 2021-03-18; просмотров: 47; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!