Уравнение движения центра масс

Модуль 1.2

ГЛАВА 2 Динамика материальной точки и системы материальных точек

Инерциальные системы отсчета. Закон инерции

Среди всевозможных систем отсчета существуют такие, относительно которых движения тел оказывается особенно простым. Тела, не подверженные воздействию других тел, движутся относительно таких систем без ускорения, т.е. прямолинейно и равномерно, или, как говорят, по инерции. Такие системы отсчета называются инерциальными.

Утверждение о существовании инерциальных систем отсчета Ньютон сформулировал в виде закона инерции, который называют также первым законом Ньютона. Согласно этому закону всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.

Опытным путем установлено, что инерциальной является система отсчета, начало которой совмещено с центром Солнца, а оси направлены на неподвижные звезды. Эта система называется гелиоцентрической (гелиос – по-гречески солнце).

Системы отсчета, движущиеся с ускорением относительно инерциальных систем, называют неинерциальными. В частности, система отсчета, связанная с Землей, неинерциальна. Однако ускорение, с которым движется Земля, настолько мало, что при решении многих задач систему отсчета, связанную с Землей, можно считать практически инерциальной.

Важной особенностью инерциальных систем отсчета является то, что по отношению к ним пространство и время обладают определенными свойствами симметрии. А именно: опыт убеждает, что в этих системах отсчета пространство однородно и изотропно, а время однородно.

Однородность и изотропность пространства заключается в том, что свойства пространства одинаковы в различных точках (однородность), а в каждой точке одинаковы во всех направлениях (изотропность).

Однородность времени заключается в том, что протекание физических явлений (в одних и тех же условиях) в разное время их наблюдения одинаково.

Основные законы динамики

Для того, чтобы сформулировать второй закон Ньютона, нужны понятия силы и массы.

Силой называется векторная величина, характеризующая воздействие на данное тело со стороны других тел.

Масса есть мера инертности тела, т.е. свойство тела «оказывать сопротивление» при любых попытках изменить его скорость – как по модулю, так и по направлению.

Импульсом тала называется векторная величина, равная произведению массы тела на его скорость.

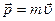. (2.1)

Второй закон Ньютона

Этот закон формулируется так.

В инерциальной системе отсчета ускорение частицы прямо пропорционально силе, действующей на частицу, и обратно пропорционально её массе

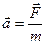. (2.2)

Отсюда

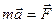. (2.2’)

Это уравнение (2.2’) называют уравнением движения материальной точки (частицы).

Учитывая, что 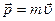, , 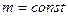можно второй закон Ньютона записать в виде:

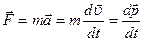Таким образом, мы получили импульсную формулировку второго закона Ньютона: скорость изменения импульса частицы равна действующей на частицу силе :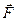

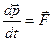. (2.2”)

Единицей силы в СИ является ньютон (Н).

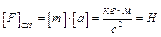Если на частицу действует насколько сил 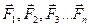, то результирующая сила

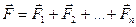тогда второй закон Ньютона можно записать так:

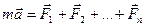. (2.3)

Направление ускорения частицы совпадает с направлением результирующей силы .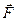

Третий закон Ньютона

Воздействие тел друг на друга всегда носит характер взаимодействия. Если тело 2 действует на тело 1 с силой 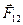, то и тело 1 действует на тело 2 с силой .

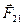Третий закон Ньютона утверждает, что силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению, т.е.

. (2.4)

Таким образом, силы всегда возникают попарно.

Силы

В классической механике приходится иметь дело с гравитационными и электромагнитными силами, а также с упругими силами и силами трения.

Гравитационные и электромагнитные силы нельзя свести к другим, более простым, силам, поэтому их называют фундаментальными. Законы фундаментальных сил просты и выражаются точными формулами.

Упругие силы и силы трения являются по своей природе электромагнитными и, следовательно, не могут считаться фундаментальными.

При решении задач нужно характеризовать силы по «источнику», вызвавшему их появление. Это означает, что за каждой силой надо видеть тело, воздействием которого обусловлена данная сила.

Приведем выражения для некоторых сил.

1. Сила гравитационного притяжения, действующая между двумя материальными точками, в соответствии с законом всемирного тяготения пропорциональна произведению масс точек 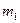и 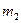, обратно пропорциональна квадрату расстояния 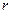между ними и направлена по прямой, соединяющей эти точки:

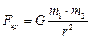, (2.5)

где 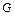– гравитационная постоянная.

2. Сила Кулона, действующая между двумя точечными зарядам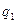и и ,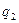

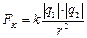, (2.6)

где 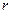– расстояние между зарядами, 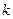– коэффициент пропорциональности, зависящий от выбора системы единиц.

В отличие от гравитационной силы кулоновская сила может быть как силой притяжения, так и силой отталкивания.

3. Сила тяжести действует на всякое тело в системе отсчета, связанной с Землей:

, (2.7)

где – масса тела, 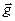– ускорение свободного падения.

4. Упругая сила – сила, пропорциональная смещению материальной точки из положения равновесия и направленная к положению равновесия:

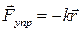, (2.8)

где 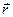– радиус - вектор характеризующий смещение частицы из положения равновесия, 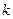– коэффициент упругости. Примером такой силы является сила упругой деформации при растяжении (сжатии) пружины или стержня, в соответствии с законом Гука 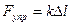, где 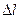– величина упругой деформации.

5. Сила трения скольжения, возникающая при скольжении данного тела по поверхности другого тела:

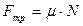, (2.9)

где 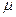– коэффициент трения скольжения, зависящий от природы и шероховатости соприкасающихся поверхностей, 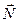– сила реакции опоры, причем 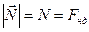, 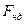– сила нормального давления, прижимающая трущиеся поверхности друг к другу.

6. Сила сопротивления, действующая на тело при его поступательном движении в газе или жидкости. При небольших скоростях сила растет пропорционально скорости:

. (2.10)

Знак минус указывает на то, что сила направлена противоположно скорости. Коэффициент 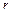называется коэффициентом сопротивления среды, он зависит от формы и размеров тела, характера его поверхности, а также от свойства среды, называемого вязкостью.

Основное уравнение динамики

Основное уравнение динамики материальной точки представляет собой математическое выражение второго закона Ньютона:

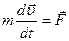. (2.11)

Уравнение (2.11) есть, по существу, дифференциальное уравнение движения точки в векторном виде. Его решение – основная задача динамики материальной точки. При этом возможны две противоположные постановки задачи.

1.Найти действующую на точку силу 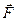, если известны масса точки и зависимость от времени ее радиуса – вектора .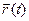

2. Найти закон движения точки, то есть зависимость от времени ее радиуса - вектора 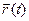, если известны масса точки, действующие на нее силы 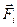(или сила 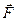) и начальные условия 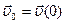и .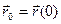

В зависимости от характера и постановки конкретной задачи решение уравнения (2.11) проводят или в векторной форме, или в координатах, или в проекциях на касательную и нормаль к траектории в данной точке.

В проекциях на оси декартовых координат

Записывая обе части уравнения (2.11) в проекциях на оси 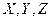получим три дифференциальных уравнения вида:

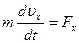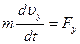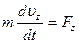, , , (2.12)

где 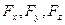– проекции вектора 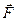на оси .

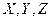Итак, на конкретном примере рассмотрим стандартный подход к решению задач с помощью уравнений (2.12).

Пример Небольшой брусок массы скользит вниз по наклонной плоскости, составляющей угол 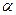с горизонтом. Коэффициент трения равен 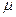. Найдем ускорение бруска.

Дано: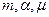

Найти: ?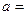

Решение:

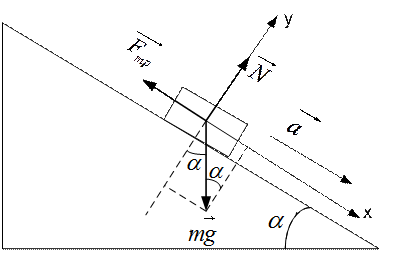
Рис.2.1

1. Следует изобразить силы, действующие на брусок. Это сила тяжести 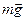, сила реакции опоры 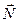, сила трения скольжения .

2. Выбрать систему координат 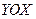, причем удобно ось 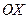совместить с направлением вектора ускорения .

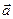3. Записать уравнение движения в векторной форме:

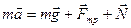
4. Записать векторное уравнение в проекциях на оси координат 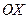и :

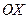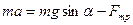
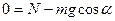
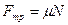
5. Решая систему трех скалярных уравнений, получим

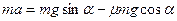
Ответ: .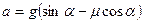

В проекциях на касательную и нормаль к траектории в данной точке

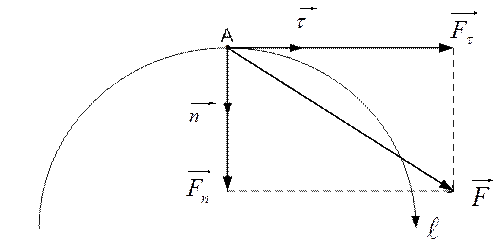
Рис. 2.2

Записывая обе части (2.11) в проекциях на подвижные орты 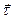и 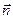(рис. 2.2) и используя полученные ранее выражения (см. формулу (1.18)) для тангенциального и нормального ускорений, получим:

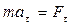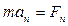(2.13)

или

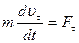
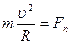, (2.14)

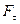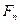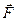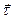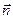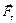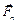где и – проекции вектора на орты и . Векторы и называют тангенциальной и нормальной составляющими силы .

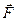Напомним, что направление орта 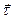выбирают в сторону возрастания дуговой координаты 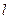, а направление орта 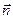– к центру кривизны траектории в данной точке.

Импульс системы

Совокупность тел, выделенных для рассмотрения, называется механической системой.

Тела системы могут взаимодействовать как между собой, так и с телами, не входящими в систему. В соответствии с этим силы подразделяются на внутренние и внешние. Внутренними называют силы, с которыми тела системы действуют друг на друга, внешними – силы, обусловленные воздействием тел, не принадлежащих системе.

Система, в которой внешние силы отсутствуют, либо векторная сумма всех внешних сил, действующих на систему, равна нулю, называется замкнутой.

Рассмотрим систему, состоящую из 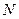частиц (материальных точек).

Обозначим через 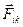силу, с которой 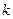-я частица действует на 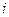-ю (см. рис.2.3).

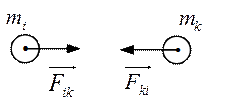Рис.2.3

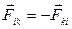Первый индекс указывает номер частицы, на которую действует сила, второй индекс – номер частицы, воздействием которой обусловлена эта сила.

Символом 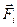обозначим результирующую всех внешних сил, действующих на 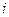-ю частицу. Напишем уравнение движения всех 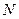частиц:

, ( )

………………………………………..

( )

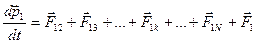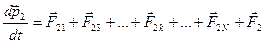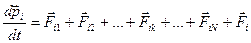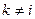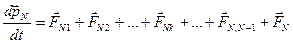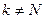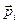( – импульс 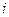- й частицы)

Сложим вместе эти уравнения. Слева получится производная по времени от суммарного импульса системы

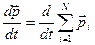справа

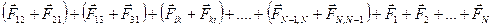Согласно третьему закону Ньютона каждая из скобок равна нулю, т.е.

, ( ).

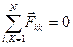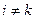Обозначим 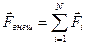– результирующая всех внешних сил.

В результате получим, что

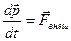. (2.15)

Таким образом, производная по времени от импульса системы равна векторной сумме всех внешних сил, действующих на тела системы.

Из уравнения (2.15) следует, что приращение импульса системы за конечный промежуток времени 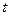есть

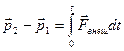, (2.16)

т.е. приращение импульса системы равно импульсу результирующей всех внешних сил за соответствующий промежуток времени.

Закон сохранения импульса

Согласно уравнению (2.15) импульс системы может изменяться под действием только внешних сил.

Если система замкнута, то внешние силы отсутствуют либо 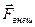равна нулю, тогда из уравнения (2.15) следует, что

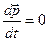и, следовательно,

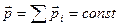(2.17)

Импульс замкнутой системы материальных точек остается постоянным. Это утверждение составляет содержание закона сохранения импульса.

В основе закона сохранения импульса лежит однородность пространства во всех точках. Параллельный перенос замкнутой системы из одного места в другое без изменения взаимного расположения и скоростей частиц не изменяет механических свойств системы. Поведение системы на новом месте будет таким же, каким оно было бы на прежнем месте.

И еще, у незамкнутой системы может сохраняться не сам импульс 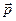, а его проекция 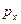на некоторое направление 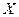. Это бывает тогда, когда проекция результирующей внешней силы 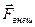, на направление 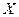равна нулю, т.е. 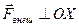. Действительно, записав уравнение (2.15) в проекции на 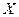, получим

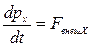откуда следует, что если 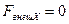, то 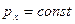. Например, при движении системы в однородном поле сил тяжести сохраняется проекция ее импульса на любое горизонтальное направление, чтобы в системе ни происходило.

Уравнение движения центра масс

В любой системе частиц имеется одна замечательная точка 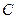, называемая центром масс, которая обладает рядом интересных и важных свойств. Ее положение относительно начала системы отсчета 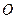характеризуется радиус-вектором.

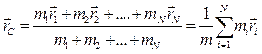(2.19)

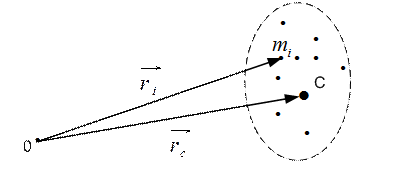
Рис. 2.4

где 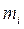и 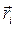– масса и радиус- вектор 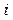-й частицы, 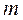– масса всей системы (рис. 2.4).

Отметим, что в однородном поле сил тяжести центр масс совпадает с центром тяжести системы.

Продифференцировав 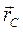по времени, найдем скорость центра масс:

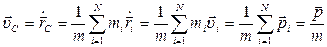. (2.20)

Отсюда следует, что

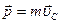, (2.21)

т.е. импульс системы равен произведению массы системы на скорость ее центра масс.

Подставив это выражение в формулу (2.15), получим уравнение движения центра масс:

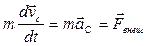. (2.22)

Таким образом, центр масс движется так, как двигалась бы материальная точка с массой, равной массе системы, под действием результирующей всех внешних сил, приложенных к телам системы. Для замкнутой системы 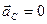. Это означает, что центр масс замкнутой системы движется прямолинейно и равномерно либо покоится.

Система отсчета, относительно которой центр масс покоится, называется системой центра масс (сокращенно ц-системой). Эта система инерциальна. Система отсчета, связанная с измерительными приборами, называется лабораторной системой (сокращенно л-системой).

Дата добавления: 2021-03-18; просмотров: 184; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!