Уравнения Пуассона и Лапласа.
Электростатическое поле
Электростатическое поле создается неподвижными (по отношению к наблюдателю) электрическими зарядами. В таком поле отсутствуют электрические токи (J=0), а, следовательно, (при отсутствии намагниченных тел) и магнитное поле (H=0; B=0).
Из полной системы уравнений электромагнитного поля для электростатического поля получаем:
; 
; 
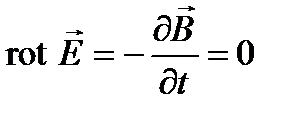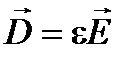
(в изотропной среде направления векторов совпадают).
В реальных устройствах объемные заряды в диэлектрике не могут находиться в покое, т.е. появляются электрические токи, что нарушат статичность поля. Поэтому во многих случаях второе уравнение имеет нулевую правую часть:
.
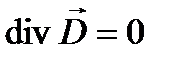Из-за равенства нулю ротора вектора напряженности электрического поля такое поле называют безвихревым.
Применяя теорему Стокса к первому уравнению, можем записать:
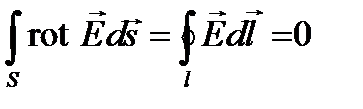
Последнее соотношение определяет независимость интеграла между фиксированными точками от пути интегрирования.
Поэтому для анализа электростатического поля удобно ввести вспомогательную скалярную функцию, называемую электрическим потенциалом. Потенциал некоторой точки поля определяется как интеграл от этой точки до точки нулевого потенциала от скалярного произведения векторов E и dl:
Потенциал точки определяется с точностью до некоторой произвольной постоянной, зависящей от выбора координат точки «p» – точки нулевого потенциала. Разность потенциалов между двумя точками не зависит от выбора точки нулевого потенциала и, конечно, от пути интегрирования.
|
|
|
.
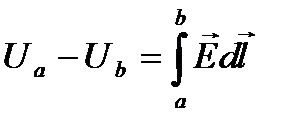При выбранном и фиксированном положении точки нулевого потенциала потенциал точки «а» зависит от координат этой точки, т.е. Ua = U (x,y,z).
Обозначим криволинейную переменную координату точки «а», лежащей на некотором расстоянии от начала координат через lа = l, а фиксированную координату точки нулевого потенциала – через l p (см. рисунок 2-1). Запишем выражение для потенциала точки с координатой l:
.
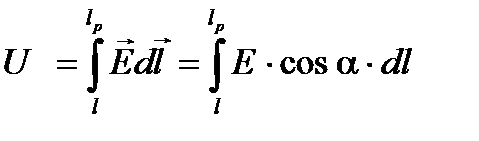Дифференцируя полученное соотношение по переменному нижнему пределу, получим:
.
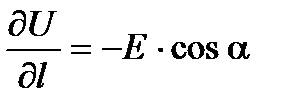p
E
a
dl
la a
lp
0
Рисунок 2–1
Скорость изменения потенциала вдоль некоторого направления равна проекции вектора напряженности электрического поля на это направление со знаком минус.
Так как потенциал точки «а» не зависит от пути интегрирования, то, проводя кривую «l» через точку «а» по разным направлениям, получим:
|
|
|
1. Проходя через точку «а» в направлении осей координат, запишем:
; 
; 
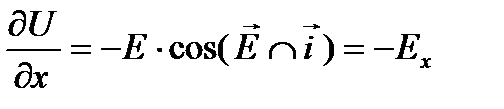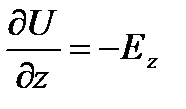
2. Проходя через точку «а» по линии l1 перпендикулярно вектору напряженности электрического поля (a1 = 900) и вдоль него по линии l2 (a2 = 0) (см. рис. 2-2), получим:
l1 E l2
a
Рисунок 2-2
; 
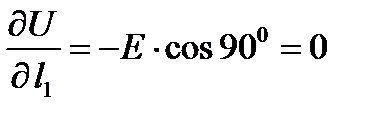При перемещении перпендикулярно вектору напряженности потенциал не изменяется, т. е. остается постоянным. Поэтому поверхности, перпендикулярные силовым линиям, называются равнопотенциальными (эквипотенциальными). Это направление обозначают через «a»
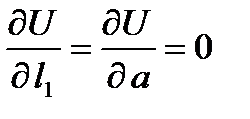
Направление вдоль линии напряженности перпендикулярно поверхности равного потенциала. Часто это направление обозначают через «n», имея в виду нормаль к равнопотенциальной поверхности, тогда последнее соотношение можно записать иначе:
.
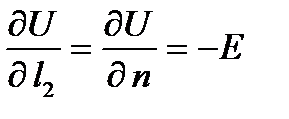Производная 
ведет себя как вектор, имеет составляющие, определяемые направляющими косинусами, и называется градиентом потенциала.
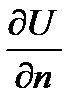® grad U = – 
.
Используя векторный оператор «набла», можем записать последнее выражение в декартовой системе координат:
|
|
|
– 
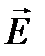= grad U = 
= 
.
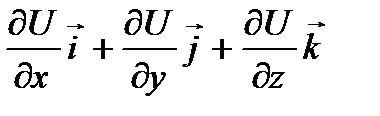Представление напряженности через потенциал позволяет свести всю совокупность уравнений электростатики, записанных для векторов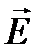 
и 
, к одному дифференциальному уравнению, относительно потенциала. Разыскание скалярной функции – потенциала, является более легкой задачей , чем определение векторных характеристик поля. Поэтому нахождение потенциала является основной задачей электростатики. По найденному потенциалу U( x, y, z) легко определяется напряженность электрического поля.
Уравнения Пуассона и Лапласа.
Преобразуем уравнения электростатического поля, выразив векторные величины через потенциал:
; 
; 
.
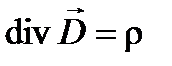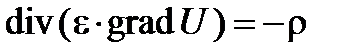Последнее уравнение справедливо в общем случае для диэлектриков с изменяющимися в пространстве свойствами – e (x, y, z). Такие случаи встречаются достаточно редко, обычно диэлектрическая проницаемость постоянна во всей рассматриваемой области, либо в отдельных ее частях.
Тогда, вынося диэлектрическую проницаемость за знак дифференциального оператора, получим:
div gradU = –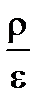 
Это уравнение называется уравнением Пуассона для скалярного электрического потенциала, записано в инвариантной форме и справедливо в любой точке поля. В декартовой системе координат, применяя оператор «набла», можем записать:
|
|
|
div gradU =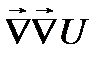 
= Ñ 2 U = 
= – 
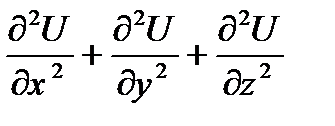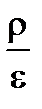= DU.
В тех точках поля, где отсутствуют свободные заряды ( r = 0), потенциал электростатического поля удовлетворяет уравнению Лапласа:
div gradU =Ñ2 U = DU = 0.
Уравнения Пуассона и Лапласа являются самыми распространенными уравнениями математической физики. Они описывают различные потенциальные поля: электростатическое поле, электрическое поле постоянных токов, магнитное поле вне областей с токами, стационарные тепловые поля, течение идеальной жидкости и др.
Рассмотрим частные решения уравнения Пуассона для различных случаев распределения зарядов.
Дата добавления: 2021-03-18; просмотров: 72; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!