Предел и непрерывность функции
Лекция №1.Функции нескольких переменных. Предел и непрерывность. Частные производные и полный дифференциал
Теоретические вопросы
1. Понятие функции многих переменных.
2. Предел и непрерывность функции многих переменных.
3. Частные производные.
4. Дифференциал функции
5. Производная сложной функции
Повторение-ТАБЛИЦА ПРОИЗВОДНЫХ И ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ!!!
Таблица производных основных функций
1. 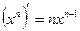 8.
8. 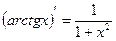
2. 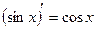 9.
9. 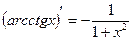
3. 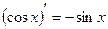 10.
10. 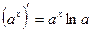
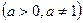
4. 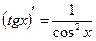 11.
11. 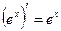
5. 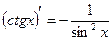 12.
12. 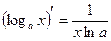
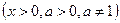
6. 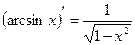

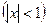 13.
13. 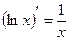
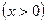
7. 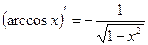

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
1. Постоянный множитель c можно выносить за знак производной:
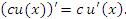
Правило 1 непосредственно вытекает из определения производной функции и свойства пределов функций, согласно которому постоянный множитель можно выносить за знак предела.
2. Если существуют производные 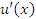 и
и 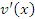 , то производная от суммы (разности) функций
, то производная от суммы (разности) функций 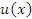 и
и 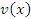 равна сумме (разности) производных:
равна сумме (разности) производных:
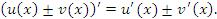
Правило дифференцирования суммы или разности функций также следует из определения производной функции и свойства пределов функций, согласно которому предел суммы (или разности) функций равен сумме (или разности) соответствующих пределов.
3. Если существуют производные 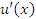 и
и 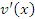 , то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
, то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
|
|
|
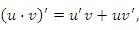
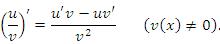
Понятие функции нескольких переменных
Если задан закон f , в силу которого каждой точке М(х 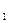 ;...;х
;...;х 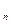 )
) 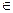 D ставится в соответствие число и, то говорят, что на множестве D определена функция нескольких переменных и= f(х
D ставится в соответствие число и, то говорят, что на множестве D определена функция нескольких переменных и= f(х 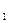 ;...;х
;...;х 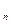 ).
).
Например, функция и= f(х 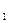 ;...;х
;...;х 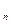 )-выражает спрос на товар.
)-выражает спрос на товар.
х1--доход потребителя, х2-цена товара, х3-расходы на рекламу, х4-вкус и предпочтения потребителя , и т. д.
Или S= S(x,y)- площадь прямоугольника со сторонами х и у –функция двух переменных .
Множество точек М(х 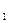 ;...;х
;...;х 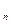 ), для которых функция и= f(х
), для которых функция и= f(х 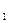 ;...;х
;...;х 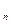 ) определена, называют областью определенияэтой функции и обозначают D(f) или ООФ.
) определена, называют областью определенияэтой функции и обозначают D(f) или ООФ.
Множество точек М, которые удовлетворяют неравенству 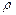 (М;М
(М;М 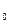 )<
)< 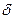 , называют
, называют 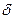 -окрестностью точки М
-окрестностью точки М 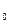 .
.
Функцией двух переменных называется закон, по которому каждой паре значений независимых переменных 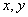 (аргументов) из области определения соответствует значение зависимой переменной
(аргументов) из области определения соответствует значение зависимой переменной 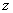 (функции).
(функции).
Данную функцию обозначают следующим образом:
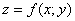 либо
либо 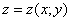 , или же другой буквой, например :
, или же другой буквой, например : 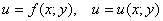
Пример : 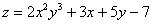 - функция 2-х переменных
- функция 2-х переменных
Геометрический смысл функции двух переменных
Если функции одной переменной 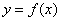 соответствует определённая линия на плоскости (например,
соответствует определённая линия на плоскости (например, 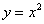 –парабола), то график функции двух переменных
–парабола), то график функции двух переменных 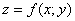 это поверхность в трехмерном пространстве .
это поверхность в трехмерном пространстве .
|
|
|
Пример на рис ниже:
Областью определения функции двух переменных 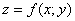 (ООФ), называется множество всех пар
(ООФ), называется множество всех пар 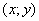 , для которых существует значение
, для которых существует значение 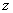 .
.
Графически область определения представляет собой всю плоскость  либо её часть.
либо её часть.
Пример 1
Найти область определения функции 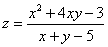
Решение: так как знаменатель не может обращаться в ноль, то:
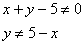
Ответ: вся координатная плоскость 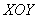 кроме точек, принадлежащих прямой
кроме точек, принадлежащих прямой 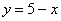
Если бы по условию требовалось выполнить чертёж, то следовало бы изобразить координатную плоскость 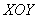 и пунктиром провести прямую
и пунктиром провести прямую 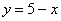 . Пунктир означает, что линия не входит в область определения. (граница области определения функции не принадлежит области определения )
. Пунктир означает, что линия не входит в область определения. (граница области определения функции не принадлежит области определения )
Пример 2
Найти область определения функции 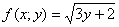
Решение: подкоренное выражение должно быть неотрицательным:
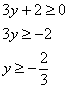
Ответ: полуплоскость 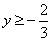
Графическое изображение здесь таково: в декартовой системе координат (х,у), сплошной линией проводим прямую 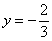 и штрихуем верхнюю полуплоскость. Сплошная линия указывает на тот факт, что она входит в область определения. (граница области определения функции принадлежит области определения )
и штрихуем верхнюю полуплоскость. Сплошная линия указывает на тот факт, что она входит в область определения. (граница области определения функции принадлежит области определения )
|
|
|
В этом случае ООФ называют замкнутой
Пример 3
Найти область определения функции и изобразить её на чертеже
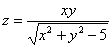
Решение: подкоренное выражение должно быть неотрицательным:
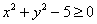 и, учитывая, что знаменатель не может обращаться в ноль, неравенство становится строгим:
и, учитывая, что знаменатель не может обращаться в ноль, неравенство становится строгим:
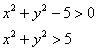
Уравнение 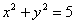 определяет окружность с центром в начале координат радиуса
определяет окружность с центром в начале координат радиуса 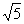 , которая делит координатную плоскость на две части – «внутренность» и «внешность» круга. Так как неравенство у нас строгое, то сама окружность не войдёт в область определения и поэтому её нужно провести пунктиром.
, которая делит координатную плоскость на две части – «внутренность» и «внешность» круга. Так как неравенство у нас строгое, то сама окружность не войдёт в область определения и поэтому её нужно провести пунктиром.
В случае, если граница не принадлежит ООФ, область называют открытой, незамкнутой.
Теперь берём произвольную точку плоскости, не принадлежащую окружности 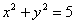 , и подставляем её координаты в неравенство
, и подставляем её координаты в неравенство 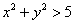 . Проще всего, конечно же, выбрать начало координат
. Проще всего, конечно же, выбрать начало координат 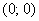 :
:
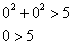
Получено неверное неравенство, таким образом, точка 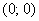 не удовлетворяет неравенству
не удовлетворяет неравенству 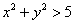 . Более того, данному неравенству не удовлетворяет и любая точка, лежащая внутри круга, и, стало быть, искомая область определения – внешняя его часть. Область определения традиционно штрихуется: см рис ниже:
. Более того, данному неравенству не удовлетворяет и любая точка, лежащая внутри круга, и, стало быть, искомая область определения – внешняя его часть. Область определения традиционно штрихуется: см рис ниже:
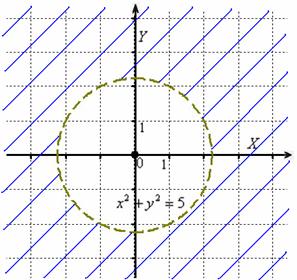
Ответ: внешняя часть круга 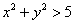
|
|
|
Линии уровня
Для лучшего понимания этого термина будем сравнивать ось 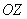 с высотой: чем больше значение «зет» – тем больше высота, чем меньше значение «зет» – тем высота меньше. Также высота может быть и отрицательной.
с высотой: чем больше значение «зет» – тем больше высота, чем меньше значение «зет» – тем высота меньше. Также высота может быть и отрицательной.
Функция 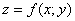 в своей области определения представляет собой пространственный график
в своей области определения представляет собой пространственный график
. Что такое линии уровня? Представим себе гористую местность . Образно говоря, линии уровня – это горизонтальные «срезы» поверхности на различных высотах. Данные «срезы» или правильнее сказать, сечения проводятся плоскостями 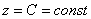 , после чего проецируются на плоскость
, после чего проецируются на плоскость 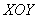 .
.
Определение:
линией уровня функции 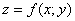 называется линия
называется линия 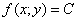 на плоскости
на плоскости 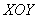 , в каждой точке которой функция сохраняет постоянное значение:
, в каждой точке которой функция сохраняет постоянное значение: 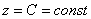 .
.
Линии уровня помогают выяснить, как выглядит та или иная поверхность – причём помогают без построения трёхмерного чертежа! Рассмотрим конкретную задачу:
Пример 4
Найти и построить несколько линий уровня графика функции
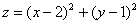
Решение: исследуем форму данной поверхности с помощью линий уровня. Запишем так: 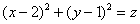
Очевидно, что в данном случае «зет» (высота) заведомо не может принимать отрицательные значения (так как сумма квадратов неотрицательна). Таким образом, поверхность располагается в верхнем полупространстве (над плоскостью 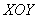 ).
).
Поскольку в условии не сказано, на каких конкретно высотах нужно «срезать» линии уровня, то мы можем выбрать несколько значений «зет» на своё усмотрение.
Исследуем поверхность на нулевой высоте, для этого поставим значение 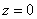 в равенство
в равенство 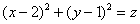 :
:
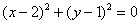
Решением данного уравнения является точка 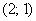 . То есть, при
. То есть, при 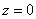 линия уровня представляет собой точку.
линия уровня представляет собой точку.
Поднимаемся на единичную высоту и «рассекаем» нашу поверхность 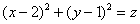 плоскостью
плоскостью 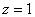 (подставляем
(подставляем 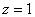 в уравнение поверхности):
в уравнение поверхности):
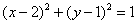
Таким образом, для высоты 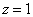 линия уровня представляет собой окружность с центром в точке
линия уровня представляет собой окружность с центром в точке 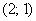 единичного радиуса.
единичного радиуса.
Теперь берём, например, плоскость 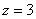 и «пересекаем » ею исследуемую поверхность
и «пересекаем » ею исследуемую поверхность 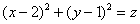 (подставляем
(подставляем 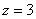 в уравнение поверхности):
в уравнение поверхности):
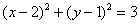
Таким образом, для высоты 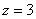 линия уровня представляет собой окружность с центром в точке
линия уровня представляет собой окружность с центром в точке 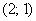 радиуса
радиуса 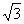 .
.
Для высоты 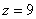 :
:
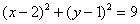 – окружность с центром в точке
– окружность с центром в точке 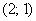 радиуса 3.
радиуса 3.
Линии уровня располагаются на плоскости  , и каждая линия подписывается – какой высоте она соответствует: z=0, z=1, z=3,……
, и каждая линия подписывается – какой высоте она соответствует: z=0, z=1, z=3,……
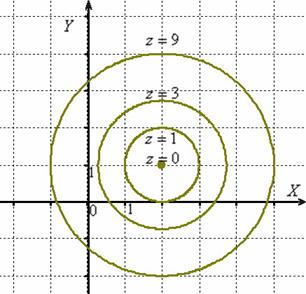
Ответ: линии уровня данной поверхности представляют собой концентрические окружности вида 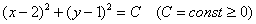
Примечание: при 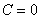 получается вырожденная окружность нулевого радиуса (точка)
получается вырожденная окружность нулевого радиуса (точка)
Само понятие линии уровня пришло из картографии. Перефразируя устоявшийся математический оборот, можно сказать, что линия уровня – это географическое место точек одинаковой высоты.
Рассмотрим гору с линиями уровня 1000, 3000 и 5000 метров:
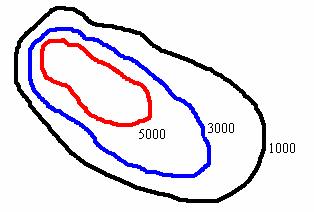
На рисунке хорошо видно, что левый верхний склон горы гораздо круче правого нижнего склона. Таким образом, линии уровня позволяют отразить рельеф местности на «плоской» карте. Кстати, здесь приобретают вполне конкретный смысл и отрицательные значения высоты – ведь некоторые участки поверхности Земли располагаются ниже нулевой отметки уровня мирового океана.
Параллели и меридианы также представляют линии уровня .
Линии уровня используют не только в картографии. Известные из курса физики изотермы , изобары, -тоже линии уровня.
Предел и непрерывность функции
Определение
Число 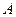 называется пределом функции
называется пределом функции 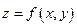 при
при 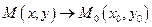 , если для любого числа
, если для любого числа 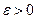 найдется такая
найдется такая 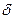 - окрестность точки
- окрестность точки 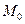 :
: 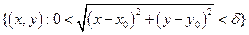 , что для любой точки
, что для любой точки 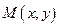 из этой окрестности имеет место неравенство:
из этой окрестности имеет место неравенство: 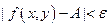 .
.
Записывают этот факт следующим образом:
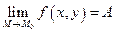 . (1)
. (1)
Заметим, что свойства пределов и действия над пределами для функции многих переменных аналогичны свойствам пределов и действиям над пределами для функции одной переменной.
Функция 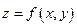 называетсянепрерывной в точке
называетсянепрерывной в точке 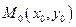 , если:
, если:
1) 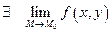 ;
;
2) 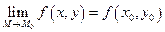 . (2)
. (2)
.
Точка 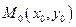 называется точкой разрыва непрерывности функции
называется точкой разрыва непрерывности функции 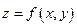 , если в этой точке функция
, если в этой точке функция 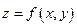 не является непрерывной, т.е. если нарушено хотя бы одно из условий определения непрерывности.
не является непрерывной, т.е. если нарушено хотя бы одно из условий определения непрерывности.
Частные производные.
Пусть функция двух переменных z = f(x;у) (для большего количества переменных всё аналогично) определена в некоторой окрестности точки М (x;у).
Дадим переменной х приращение 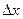 так, чтобы точка (х+
так, чтобы точка (х+ 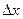 ;у) принадлежала этой окрестности. При этом функция z = f(x;у) изменится на величину
;у) принадлежала этой окрестности. При этом функция z = f(x;у) изменится на величину
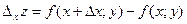 ,
,
которая называется частным приращением функции z = f(x;у) по переменной х.
Аналогично, величину
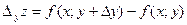
называют частным приращением функции по переменной у.
Определение
Если существует предел
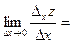
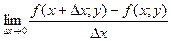 ,
,
то его называют частной производной функции z = f ( x ;у) в точке М ( x ;у) по переменной х и обозначают такими символами:
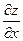 ,
, 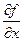 ,
, 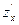 ,
, 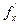 .
.
Аналогично
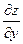 =
= 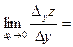
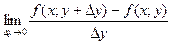 .
.
Частная производная — это предел отношения приращения функции по выбранной переменной к приращению этой переменной, при стремлении этого приращения к нулю.
Из таких определений следует, что правила вычисления производных, совпадают с правилами дифференцирования функций одной переменной. Следует только помнить, что при вычислении частной производной по одной переменной остальные переменные считаются постоянными.
Частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей.
Обозначения частных производных первого порядка:
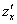 или
или 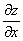 – частная производная по «икс»
– частная производная по «икс»
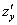 или
или 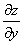 – частная производная по «игрек»
– частная производная по «игрек»
ПРАВИЛО :
Когда находят частную производную по « икс», то переменную 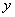 считают константой (постоянным числом).
считают константой (постоянным числом).
Когда находят частную производную по « игрек», то переменную х считают константой (постоянным числом).
Далее применяют формулы и правила дифференцирования функции одной переменной
Пример 5
Найти частные производные функции
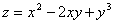 ,
,
Решение:
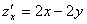 ,
,
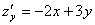 ,
,
Пример 6
Найти частные производные первого порядка функции 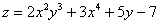
Решение:
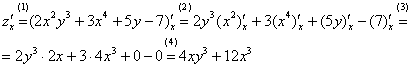
(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.
(2) Используем правила дифференцирования 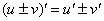 ,
, 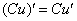 . Обратите внимание на первое слагаемое: так как
. Обратите внимание на первое слагаемое: так как 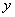 считается константой, а любую константу можно вынести за знак производной, то
считается константой, а любую константу можно вынести за знак производной, то 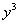 вместе с множителем 2 мы выносим за скобки.
вместе с множителем 2 мы выносим за скобки.
(3) Далее используем табличные производные 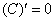 и
и 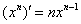
(4) Упрощаем ответ.
Теперь найдем 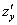 в соответствии с правилом
в соответствии с правилом
Когда мы находим частную производную по «игрек», то переменная 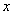 считается константой (постоянным числом).
считается константой (постоянным числом).
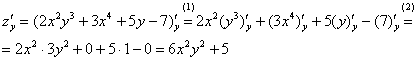
(1) Используем те же правила дифференцирования 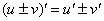 ,
, 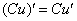 . В первом слагаемом выносим константу
. В первом слагаемом выносим константу 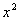 за знак производной, во втором слагаемом ничего вынести нельзя поскольку
за знак производной, во втором слагаемом ничего вынести нельзя поскольку 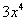 – уже константа.
– уже константа.
(2) Используем таблицу производных элементарных функций
Дата добавления: 2021-03-18; просмотров: 128; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
