Алгоритм нахождение условного экстремума функции двух переменных.
Покажем на конкретном примере
Пример 1. Найти условные экстремумы функции двух переменных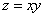 
, выражающей площадь прямоугольника через его стороны x и y при условии 
, означающем, что существует верёвка, которой можно ограничить этот прямоугольник, и длина этой верёвки равна 100.
Решение
Шаг 1. Приведём уравнение условия связи к требуемому виду с нулём в правой части:
.
Шаг 2. Вводится функция Лагранжа
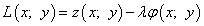, В нашем примере:
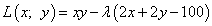
где первое слагаемое - сама исходная функция, а второе слагаемое со знаком минус - левая часть уравнения условия связи, умноженная на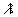 
(лямбда) - множитель Лагранжа.
Шаг 3. Находим частные производные по х, у и 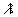и приравниваем их к нулю (необходимый признак существования условного экстремума):
Решения этой системы уравнений являются точками возможного условного экстремума - стационарными точками или, как ещё говорят, критическими точками.
В нашем примере :
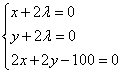
Из первого и второго уравнений выразим соответственно x и y:
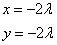
Подставим эти выражения в третье уравнение и найдём значение множителя Лагранжа:
Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции:
Получил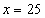и 
и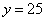 
. Эти значения являются также координатами стационарной точки. Таким образом, получили стационарную точку 
.
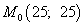Шаг 4. Пусть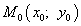 
является стационарной точкой, найденной на шаге 3. Чтобы определить, является ли условный экстремум минимумом или максимумом, нужно найти второй дифференциал функции Лагранжа
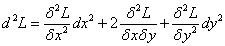
и в полученном выражении подставить вместо "лямбды" её значения (значения множителя Лагранжа), найденные на шаге 2.
Если значение второго дифференциала функции Лагранжа меньше нуля (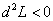 
), то стационарная точка является точкой максимума, если больше нуля ( 
), то стационарная точка является точкой минимума.
Если значение второго дифференциала функции Лагранжа равно нулю, то требуются дополнительные исследования, но такие случаи практически не попадаются в задачах, задаваемых студентам.
Координаты стационарных точек подставляются в исходную точку и, таким образом, мы окончательно находим условные экстремумы (или минимум и максимум или что-то одно из этих экстремумом).
В нашем примере:
Найдём второй дифференциал функции Лагранжа:
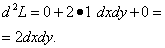
В нашем случае, так как первое и третье составляющие равны нулю, нам не придётся подставлять в них значения множителя Лагранжа. Зато нужно найти отношения между дифференциалами dx и dy:
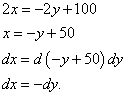
Так как полученные значения - противоположные по знаку, то получаем, что в любом случае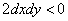 
.
Теперь можем найти значение условного экстремума исходной функции, являющееся максимумом:
.
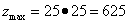Это заданная исходной функцией максимальная площадь прямоугольника, который можно ограничить верёвкой, длина которой равна 100.
Пример 2. Найти условные экстремумы функции двух переменных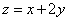 
при условии 
.
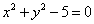Решение.
Шаг 1. Составим функцию Лагранжа:
.
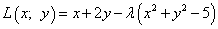Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:
Из первого и второго уравнений выразим соответственно x и y:
Подставим эти выражения в третье уравнение и найдём значения множителя Лагранжа:
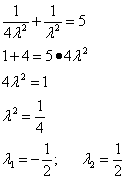
Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции при двух значениях множителя Лагранжа:
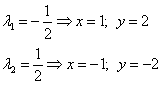
Эти значения икса и игрека являются координатами двух стационарных точек. Таким образом, получили стационарные точки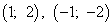 
.
Шаг 3. Найдём частные производные второго порядка функции Лагранжа:
:
Найдём второй дифференциал функции Лагранжа по формуле
:
.
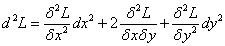Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа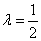 
:
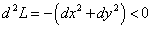
Получили значение, меньшее нуля, следовательно, точка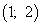 
- точка условного максимума:
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа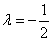 
:
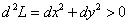
Получили значение, большее нуля, следовательно, точка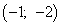 
- точка условного минимума:
.
Таким образом, условные экстремумы заданной функции найдены.
Практический пример
При формировании годового бюджета администрации города N предстоит распределить сумму в 15 млрд. рублей между вложениями:
-в ремонт и развитие транспортных коммуникаций (дороги, общественный транспорт и т.п.);
-в коммунальное хозяйство.
Полезность вложений может быть аппроксимирована функцией:
U = –x2 + 40x –y2 + 30y,
где
x - сумма, выделенная на поддержание коммунального хозяйства в млрд. рублей, x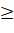 
0;
y - сумма, вложенная в ремонт и развитие транспортных коммуникаций в млрд. рублей, y 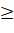0.
Как распределить 15 млрд. рублей финансирования из условия достижения наибольшего уровня полезности?
Решение
Имеем задачу на условный экстремум. Нужно найти максимум функции U(x,y) при бюджетных ограничениях
x + y = 15 млрд. рублей. (1)
Составляем функцию Лагранжа:
F= U(x,y)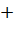 
λΨ (x,y) = –x2 + 40x –y2 + 30y + λ (x + y– 15),
где λ ― множитель Лагранжа.
Записываем необходимые условия существования экстремума функции Лагранжа:
(2)
Решение системы (2) дает:
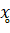=10; 
=5; λ°= 
20 .
Убедимся, что при найденном решении имеет место условный максимум.
Составим определитель:
|
Δ =
|
| = |
( 
, 
)
( 
( 
)
( 
( 
(
|
=
|
|
=  4 < 0 => Max.
|
Дата добавления: 2021-03-18; просмотров: 59; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!
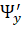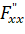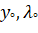
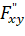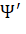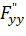