Алгоритм нахождения экстремумов функции двух переменных
Дана функция двух переменных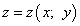 
.
Шаг 1. Находим частные производные 1 порядка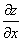 
и 
.
Шаг 2. Приравниваем частные производные 1 порядка 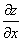и нулю (необходимый признак существования экстремума):
Решения этой системы уравнений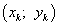 
являются точками возможного экстремума - критическими точками.
Шаг 3. Пусть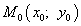 
является критической точкой, найденной на шаге 2. Чтобы убедиться, что в ней существует экстремум функции двух переменных, находим частные производные второго порядка 
Шаг 4. Обозначим частные производные второго порядка :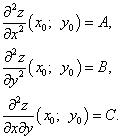 
И составляем определитель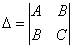 
Шаг 5
Находим определитель 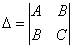и проверяем достаточный признак существования экстремума:
Если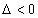 
, то экстремума в найденной критической точке нет,
если 
, то экстремум в найденной критической точке есть,
если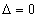 
, то требуются дополнительные исследования.
Если экстремум в найденной точке есть и если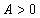 
, то в этой точке существует минимум функции двух переменных, если 
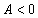, то максимум.
Шаг 6. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных 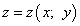и получаем значение экстремума функции двух переменных (минимума или максимума).
Пример 1. Найти экстремумы функции двух переменных 
.
Решение. Следуем изложенному выше алгоритму.
Шаг 1. Находим частные производные 1 порядка 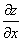и .
.
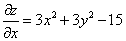
Шаг 2. Составляем систему уравнений из равенств этих производных нулю:
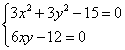
Делим первое уравнение системы на 3, а второе на 6 и получаем
|
|
|
Из второго уравнения выражаем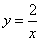 
, подставляем в первое уравнение и получаем
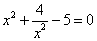
Умножаем это уравнение на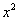 
и получаем
.
Производим замену переменной: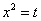 
и получаем
.
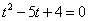Решаем полученное квадратное уравнение : 
.
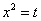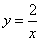Так как и , то
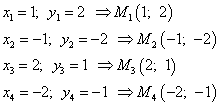
Таким образом, получили четыре критических точки - точки возможного экстремума.
Шаг 3. Находим частные производные второго порядка
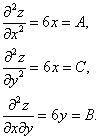
И составляем определитель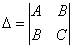
Шаг 4. Находим определитель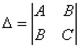 
:
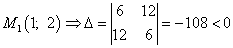, т. е. экстремума в найденной критической точке нет,
, т. е. экстремума в найденной критической точке нет,
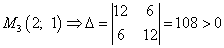и 
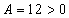, т. е. в найденной критической точке есть минимум функции двух переменных,
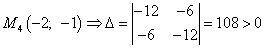и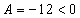 
, т. е. в найденной критической точке есть максимум функции двух переменных.
Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значения экстремума функции двух переменных:
,
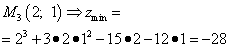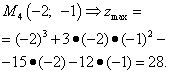
Пример 2. Найти экстремумы функции двух переменных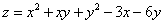 
.
Шаг 1. Находим частные производные:
.
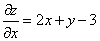
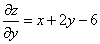Шаг 2. Составляем систему уравнений из равенств этих производных нулю:
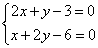
Решаем систему уравнений:
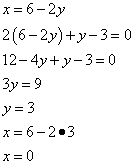
Таким образом, получили критическую точку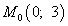 
- точку возможного экстремума.
Шаг 3. Находим частные производные второго порядка
|
|
|
И составляем определитель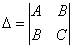
Шаг 4. Находим определитель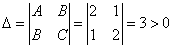 
, т. е. в найденной критической точке есть экстремум, причём так как 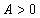, то это минимум.
Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значение экстремума функции двух переменных:
.
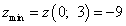Условный экстремум
Если возникает необходимость найти экстремумы функции нескольких переменных 
при условии, что существует связь между переменными этой связи, заданная уравнением 
. В этом случае говорят, что требуется найти условный экстремум.
Дата добавления: 2021-03-18; просмотров: 54; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!