Числовые характеристики дискретных случайных величин
Пусть x — дискретная случайная величина со значениями 
и их вероятностями рi = P(x= 
i = 1, 2, ..., n.
Математическим ожиданием (или средним значением) дискретной случайной величины x называется число
.
Если множество значений случайной величины x бесконечно (т.е. счетно), то математической ожидание определяется как бесконечный ряд
в случае, когда он абсолютно сходится. Если x – по-прежнему дискретная величина и j(х) — некоторая функция, то математическое ожидание величины
h = j(x) можно вычислить по формуле
при условии (в бесконечном случае), что ряд, стоящий справа, абсолютно сходится.
Математическое ожидание обладает следующими свойствами:
1) МC= C (C – константа);
2) М(Cx) = CМx для любой константы C;
3) М(x+h) = Мx + Мh;
4) М(xh) = (Мx)(Мh), если x и h независимы.
Если заданы совместное распределение вероятностей случайных величин x и h и функция j(x,y) двух аргументов, то
.
Дисперсией случайной величины x называется число Dx=М(x-Мx)2. Величина s= 
называется среднеквадратическим отклонением.
Из определения дисперсии вытекает формула для вычисления дисперсии дискретной случайной величины:
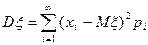
при условии абсолютной сходимости ряда. Однако чаще удобнее бывает вычислять дисперсию по другой формуле:
Dx=Мx2–(Мx)2
Для дисперсии справедливы следующие свойства.
1) DC=0 (дисперсия постоянной равна нулю);
2) D(Cx)=C2Dx;
3) D(x+C)=Dx.
4) Если случайные величины x и h независимы, то D(x+h)=Dx+Dh.
|
|
|
Задача 4. Пусть случайная величина имеет следующий закон распределения
| x | -1 | 0 | 2 |
| P | 1/4 | 1/4 | 1/2 |
Вычислить математическое ожидание Mx, дисперсию Dx и среднеквадратическое отклонение s.
Решение. По определению математическое ожидание x равно
.
Далее, 
, а потому 
.
Среднеквадратическое отклонение 
.
Задача 5. Для пары случайных величин из задачи 3 вычислить 
.
Решение. Пользуемся формулой, указанной выше. А именно, в каждой клетке таблицы выполняем указанную операцию (т.е. умножение значений 
и 
) и результат умножаем на вероятность в клетке, и все это суммируем по всем клеткам таблицы. В итоге получаем:
Ковариацией случайных величин x и h называется число
cov(x,h)=М[(x-Мx)(h-Мh)]
(в предположении существования конечных математических ожиданий).
Из определения ковариации вытекают следующие ее свойства:
1. Если x и h - независимые случайные величины, то 
Обратное неверно. Если 
, то случайные величины x и h называются некоррелированными. Из некоррелированности не вытекает независимости.
2. 
;
3. 
; 
;
4. 
и 
5. 
6. Если случайные величины x1 и x2 имеют конечные дисперсии Dx1 и Dx2, то дисперсия суммы этих случайных величин существует и равняется
|
|
|
D(x1+x2)=Dx1+Dx2+2cov(x1,x2).
Этими свойствами удобно пользоваться при вычислении ковариации от сложных выражений. Например,
Обычно ковариацию вычисляют по более простой формуле:
cov(x,h)=М(xh)–(Мx)(Мh).
Задача 6. Для пары случайных величин из задачи 3 вычислить ковариацию cov(x,h).
Решение. В предыдущей задаче уже вычислено математическое ожидание 
. Осталось вычислить 
и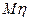 
. Используя полученные в решении задачи 3 частные законы распределения, получаем
, и, значит,
.
и h.
Дата добавления: 2021-03-18; просмотров: 92; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!