Примеры дискретных случайных величин
Глава 5. Дискретные случайные величины
Случайная величина и ее закон распределения.
Случайной величиной x называется любая действительная функция x=x(w), wÎW, определенная на пространстве элементарных событий W. Если множество значений такой функции конечно или счетно, то такую случайную величину называют дискретной. В результате опыта случайная величина может принять то или иное значение, причем заранее неизвестно, какое именно.
Например. При двукратном подбрасывании монеты возможны следующие исходы: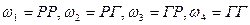 
, т.е. пространство элементарных событий имеет вид 
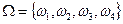, причем каждый элементарный исход имеет вероятность ¼. Пусть x(w) – число выпадений герба при двукратном бросании монеты, тогда x(w1)=0, x(w2)=1, x(w3)=1, x(w4)=2. Зная вероятности для элементарных исходов, можно вычислить вероятности для соответствующих значений случайной величины x:
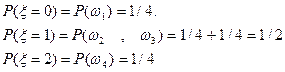
Полученные вероятности можно свести в таблицу(в первой строке перечислены значения случайной величины, а второй – их вероятности):
| x | 0 | 1 | 2 |
| P | 1/4 | ½ | ¼ |
Такая таблица уже не содержит информацию о том, на каком вероятностном пространстве определена случайная величина, в ней приведены лишь значения случайной величины (в первой строке) и их вероятности (во второй строке).
Законом (или рядом) распределения дискретной случайной величины x называется таблица, в которой перечислены все возможные значения x1, x2,…, xn этой случайной величины и соответствующие им вероятности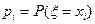 
:
|
|
|
| x | x1 | x2 | … | xn |
| P | p1 | p2 | … | pn |
Здесь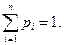 
Если множество значений случайной величины счетно, то эта таблица является бесконечной справа, а сумма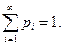 
Задача 1. В связке из 3 ключей только один ключ подходит к двери. Ключи перебирают до тех пор, пока не отыщется подходящий ключ. Построить закон распределения для случайной величины x – числа перепробованных ключей.
Решение. Число перепробованных ключей может равняться 1, 2, 3. Если испытали только один ключ, это означает, что этот первый ключ сразу подошел к двери, а вероятность такого события равна 1/3. Итак,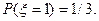 
Далее, если перепробованных ключей было 2, т.е. x=2, это значит, что первый ключ не подошел, а второй – подошел. Вероятность этого события равна 2/3×1/2=1/3. То есть, 
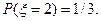Аналогично вычисляется вероятность 
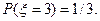В результате получается следующий закон распределения:
| x | 1 | 2 | 3 |
| P | 1/3 | 1/3 | 1/3 |
Функция распределения
Функцией распределения случайной величины x называется функция Fx(x), определенная для любого действительного х и выражающая вероятность того, что случайная величина x примет значение, меньшее х:
Fx(x)=P(x<x).
Функция распределения обладает следующими свойствами:
|
|
|
1. Для любого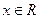 
справедливо неравенство 0£Fx(x)£1.
2. Функция распределения является неубывающей функцией, то есть, если Fx(x1) ≤ Fx(x2), если х2<х1.
3. Вероятность того, что случайная величина примет значение из полуинтервала [x1,x2), равна разности значений функции распределения на концах интервала, то есть P(x1£x<x2)=Fx(x2)-Fx(x1).
4. Если возможные значения случайной величины расположены на всей числовой прямой, то справедливы следующие предельные соотношения
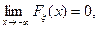
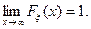
5. Функция распределения непрерывна слева, то есть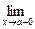 
Fx(x)=F(a).
6. Справедливо равенство: P(x³x)=1-Fx(x).
Задача 2.Построить функцию распределения Fx(x) для случайной величины x из задачи 1.
Решение. Случайная величина x имеет три значения 1, 2, 3, которые делят всю числовую ось на четыре интервала: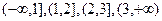 
. Если x≤1, то неравенство x<x невозможно (левее x нет значений случайной величины x) и значит, для такого x функция Fx(x)=0.
Если 1<x≤2, то неравенство x<x возможно только если x=1, а вероятность такого события равна 1/3, поэтому для таких x функция распределения Fx(x)=1/3.
Если 2<x≤3, неравенство x<x означает, что или x=1, или x=2, поэтому в этом случае вероятность P(x<x)=P(x=1)+P(x=2)=2/3, т.е. Fx(x)=2/3.
|
|
|
И, наконец, в случае x>3 неравенство x<x выполняется для всех значений случайной величины x, поэтому P(x<x)=P(x=1)+P(x=2)+P(x=3)==1, т.е. Fx(x)=1.
Итак, мы получили следующую функцию:
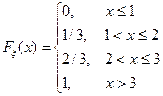
Примеры дискретных случайных величин
Распределение Бернулли (или биномиальное распределение) определяется как закон распределения случайной величины, равной числу успехов в n испытаниях Бернулли. Эта случайная величина x может принять любое из значений 0, 1, 2, …, n, а их вероятности определяются формулой Бернулли: если p – вероятность успеха, q – вероятность неудачи, то
, 
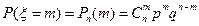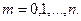
Распределение Пуассона. Случайная величина, распределенная по закону Пуассона, может принять любое из значений 0, 1, 2, … (счетное множество значений), а их вероятности задаются формулой
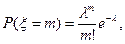
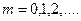, l>0.
Геометрическое распределение имеет случайная величина x, равная числу испытаний Бернулли до первого «успеха» (включительно) с вероятностью «успеха» в одном испытании равном р. Такая случайная величина принимает значения x=1, 2, 3,…, а их вероятности задаются формулой:
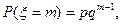
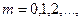
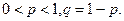
Гипергеометрическое распределение определяется, например, в задаче о выборке деталей. Пусть имеется N деталей, из которых M – стандартные. Делается выборка из n деталей. Случайная величина x определяется как число стандартных деталей в такой выборке. Оно может равняться любому числу от 0 до n, но, конечно, не больше, чем М, т.е. m=0,1,2,…,min(n,M). Вероятности этих значений определяются гипергеометрической формулой
|
|
|
, 
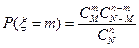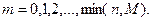
Дискретный случайный вектор.
Пусть на одном и том же пространстве элементарных исходов W заданы две случайные величины x и h, принимающие значения хi (i = 1, 2,...) и уj (j = 1, 2,...), соответственно. Упорядоченная пара (x,h) называется случайным вектором или двумерной случайной величиной. Совместный закон распределения вероятностей дискретных величин x и h задается вероятностями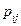 
одновременного осуществления событий {x = хi} и {h = уj}: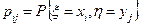 
и представляется в виде таблицы
| x h | y1 | y2 | … | ym |
| x1 |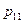 
| 
| … | 
|
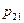
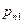
| x2 |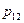 
| 
| … | 
|
| … | … | … | … | … |
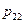
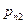
| xn |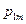 
| 
| … | 
|
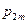
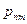
При этом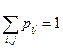 
.
Вероятность события типа {(x, h)ÎВ} — «случайная точка (x,h) попадает в заданную область В» — вычисляется по формуле
,
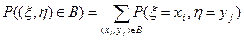т.е. суммирование идет по всем возможным парам (хi, yj) значений случайных величин x,h, для которых соответствующая точка (xi yj) входит в область В.
Частным законом распределения случайной величины x называется вероятность события {x = хi}. Если задан совместный закон распределения, то частный закон распределения для x можно получить с помощью формулы:
.
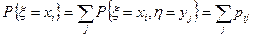Аналогично, частным законом распределения h называется вероятность события {h = yi}, которую также можно вычислить с помощью формулы:
.
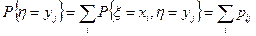Дискретные случайные величины x, h называются независимыми, если их совместный закон распределения представляется в виде произведения их частных законов распределения:
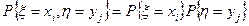для всех значений хi и уj,
то есть если независимы случайные события {x = хi} и {h = уj}.
Задача 3. Совместный закон распределения случайных величин x и h задан c помощью таблицы
| x h | 1 | 2 |
| -1 | 1/16 | 3/16 |
| 0 | 1/16 | 3/16 |
| 1 | 1/8 | 3/8 |
Вычислить частные законы распределения составляющих величин x и h, определить, зависимы ли они? Вычислить вероятность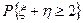 
.
Решение. Частное распределение для x получается суммированием вероятностей в строках:
;
;
.
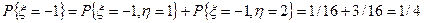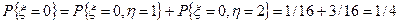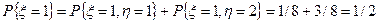Аналогично получается частное распределение для h:
;
.
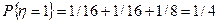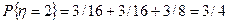Полученные распределения можно записать в ту же таблицу напротив соответствующих значений случайных величин:
| x h | 1 | 2 | |
| -1 | 1/16 | 3/16 | ¼ |
| 0 | 1/16 | 3/16 | ¼ |
| 1 | 1/8 | 3/8 | ½ |
| 1/4 | 3/4 |
Теперь ответим на вопрос о независимости случайных величин x и h. Для этого в каждой клетке совместного распределения вычислим произведение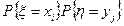 
и сравним его со значением вероятности 
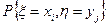в этой клетке. Например, в клетке для значений x=-1 и h=1 стоит вероятность 1/16, а произведение соответствующих частных вероятностей 1/4×1/4 равно 1/16, т.е. совпадает с совместной вероятностью. Это условие проверяется во всех оставшихся пяти клетках, и оно оказывается верным во всех этих клетках. Следовательно, случайные величин x и h независимы.
Для вычисления вероятности 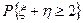отметим клетки, для которых выполнено условие 
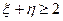. Таких клеток всего три, и соответствующие вероятности в этих клетках равны 1/8, 3/16, 3/8. Их сумма равна 11/16, это и есть искомая вероятность. Формально вычисление этой вероятности можно записать так:
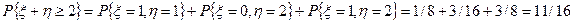
Дата добавления: 2021-03-18; просмотров: 146; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!