Приближенные вычисления с помощью дифференциала функции одной переменной
Пример 1Вычислить приближенно 
, заменяя приращения функции ее дифференциалом.
Решение: формула для приближенных вычислений: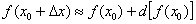 
На первом этапе необходимо составить функцию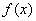 
. По условию предложено вычислить кубический корень из числа: , поэтому соответствующая функция имеет вид: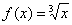 
. Нам нужно с помощью формулы найти приближенное значение 
.
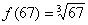Смотрим на левую часть формулы 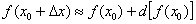- число 67 необходимо представить в виде 
. Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе: 
– получилось 4 с хвостиком, это важный ориентир для решения.
В качестве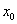 
подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение 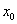должно быть как можно ближе к 67. В данном случае: 
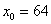. Действительно: 
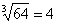. Если 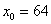, то приращение аргумента: 
.
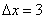Итак, число 67 представлено в виде суммы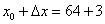 
Далее работаем с правой частью формулы .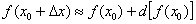
Сначала вычислим значение функции в точке .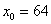 
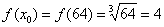
Дифференциал в точке находится по формуле: 
.
Из формулы следует, что нужно взять первую производную:
И найти её значение в точке :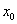 
Таким образом: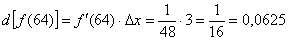 
Согласно формуле :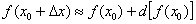 
Найденное приближенное значение достаточно близко к значению 
, вычисленному с помощью микрокалькулятора. Ответ: 
Пример 2 Вычислить приближенно с помощью дифференциала значение функции 
в точке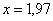 
. Вычислить более точное значение функции в точке 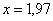с помощью микрокалькулятора, оценить абсолютную и относительную погрешность вычислений.
|
|
|
Фактически то же самое задание, его запросто можно переформулировать так: «Вычислить приближенное значение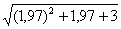 
с помощью дифференциала»
Решение: Используем знакомую формулу: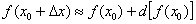
В данном случае уже дана готовая функция: 
. Значение 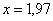необходимо представить в виде 
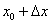. Число 1,97 очень близко к «двойке», поэтому напрашивается 
. И, следовательно: 
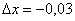. Вычислим значение функции в точке : 
Используя формулу , вычислим дифференциал в этой же точке. Находим первую производную: 
И её значение в точке : 
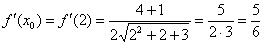
Таким образом, дифференциал в точке: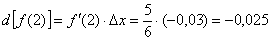 
В результате, по формуле :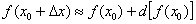 
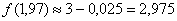
Вторая часть задания состоит в том, чтобы найти абсолютную и относительную погрешность вычислений.
Абсолютная погрешность вычислений находится по формуле:
Знак модуля показывает, что нам без разницы, какое значение больше, а какое меньше. Важно, насколько далеко приближенный результат отклонился от точного значения в ту или иную сторону.
Относительная погрешность вычислений находится по формуле:
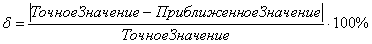, или, то же самое:
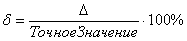
Относительная погрешность показывает, на сколько процентов приближенный результат отклонился от точного значения.
Вернемся к задаче, в которой вычислили приближенное значение функции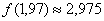 
с помощью дифференциала.
|
|
|
Вычислим точное значение функции с помощью микрокалькулятора:
.
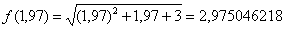Вычислим абсолютную погрешность: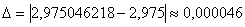 
Вычислим относительную погрешность: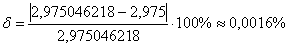 
, получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение.
Ответ: 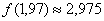, абсолютная погрешность вычислений 
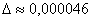, относительная погрешность вычислений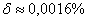 
Дата добавления: 2021-03-18; просмотров: 165; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!