Почему дифференциал можно использовать в приближенных вычислениях?
Дифференциал, 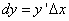 является главной, линейной относительно
является главной, линейной относительно 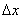 частью приращения функции; чем меньше
частью приращения функции; чем меньше 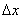 , тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях
, тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях 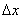 (и при
(и при  ) приращение функции можно приближенно заменить его главной частью
) приращение функции можно приближенно заменить его главной частью 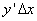 , т.е.
, т.е. 
О разных формах записи дифференциала
Дифференциал функции в точке x и обозначают так: 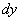 или
или  Следовательно,
Следовательно,
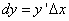 или
или  или же
или же 
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента, а 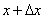 - наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме: 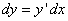 или
или 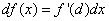
Пример 1. Найти дифференциалы функций:
1) 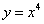 ; 2)
; 2) 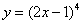 ; 3)
; 3) 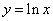 ; 4)
; 4) 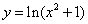 .
.
Решение. Применяя формулы дифференцирования степенной и логарифмической функций из таблицы производных, а также формулы, находим:
1) 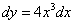 ; 2)
; 2) 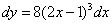 ; 3)
; 3) 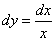 ; 4)
; 4) 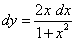 .
.
Пример 2. Найти дифференциал функции 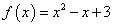 в точке x = 2,
в точке x = 2,
1) выделив линейную часть;
2) по формуле.
Решение: 1) Находим приращение функции в точке x = 2:
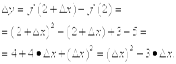 Линейная часть составляет
Линейная часть составляет 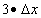 и, таким образом,
и, таким образом, 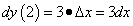 .
.
2) Используем формулу 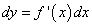 :
:
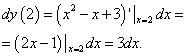
Пример 3. Найти дифференциал функции
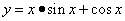 в точке x.
в точке x.
Решение: 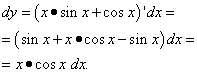
|
|
|
Пример 4. Найти дифференциал функции  в точках x = 0 и x = 1.
в точках x = 0 и x = 1.
Решение: 
Свойства дифференциала
Дифференциал обладает свойствами, аналогичными свойствам производной:
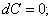 (С – постоянная величина)
(С – постоянная величина) 
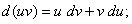
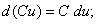
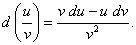
Формулы получаются из соответствующих формул для производной умножением обеих частей каждого равенства на  .
.
Дифференциал сложной функции
Рассмотрим дифференциал сложной функции. Пусть y сложная функция x: 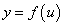 ,
,  . Дифференциал
. Дифференциал 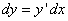 этой функции, используя формулу для производной сложной функции, можно записать в виде
этой функции, используя формулу для производной сложной функции, можно записать в виде 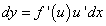 . Но
. Но 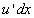 есть дифференциал функции u, поэтому
есть дифференциал функции u, поэтому 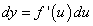 , т. е.
, т. е. 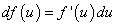 .
.
Здесь дифференциал записан в том же виде, как и в формуле для дифференциала функции независимой переменной x, т. е. 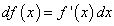 , хотя аргумент u является не независимой переменной, а функцией x.
, хотя аргумент u является не независимой переменной, а функцией x.
Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливо независимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называется инвариантностью (неизменностью) формы дифференциала.
Во всех примерах требуется вычислить дифференциал функции двумя способами: выражая его через dx и через du - дифференциал промежуточной переменной u. Проверить совпадение полученных результатов.
|
|
|
Пример 5. Дана функция 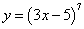 . Решение.
. Решение.
Через dx: 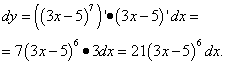
Использовали правило дифференцирования степенной функции.
Через du: 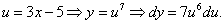
Подставляя в полученное равенство 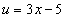 и
и 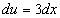 , получаем
, получаем
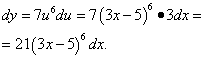 Результаты совпадают.
Результаты совпадают.
Пример 6. Дана функция 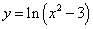 . Решение.
. Решение.
Через dx: 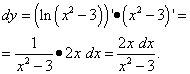 Использовали общее правило дифференцирования сложной функции и правило дифференцирования сложной логарифмической функции.
Использовали общее правило дифференцирования сложной функции и правило дифференцирования сложной логарифмической функции.
Через du:  .Подставляя в полученное равенство
.Подставляя в полученное равенство  и
и 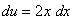 , получаем
, получаем 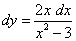 . Результаты совпадают.
. Результаты совпадают.
Дата добавления: 2021-03-18; просмотров: 117; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
