Пара непрерывных случайных величин
Пусть заданы две непрерывные случайные величины x и h. Тогда пара (x, h) определяет «случайную» точку на плоскости. Пару (x, h) называют случайным вектором или двумерной случайной величиной.
Совместной функцией распределения случайных величин x и h и называется функция F(x,y)=P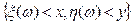 
, т.е. вероятность попадания случайного вектора (x, h) в бесконечный угол на плоскости с вершиной в точке (x,y) лежащий ниже и левее этой точки, т.е. функция 
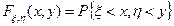. Совместной плотностью распределения вероятностей случайных величин x и h называется функция 
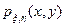такая, что 
.
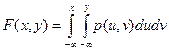Смысл такого определения совместной плотности распределения заключается в следующем. Вероятность того, что «случайная точка» (x,h) попадет в область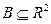 
на плоскости, вычисляется как объем трехмерной фигуры – «криволинейного» цилиндра, ограниченного поверхностью 
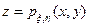и плоскостью z=0, и основанием которого является множество B. Аналитически этот факт записывается с помощью двойного интеграла:
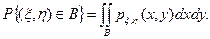
Простейшим примером совместного распределения двух случайных величин является двумерное равномерное распределение на множестве A . Пусть задано ограниченное множество М с площадью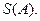 
Оно определяется как распределение пары (x, h), задаваемое с помощью следующей совместной плотности:
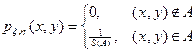
Задача 5.Пусть двумерный случайный вектор (x, h) равномерно распределен внутри треугольника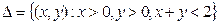 
. Вычислить вероятность неравенства x>h.
Решение. Площадь указанного треугольника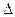 
равна 
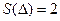(см. рис. № ?). В силу определения двумерного равномерного распределения совместная плотность случайных величин x, h равна
|
|
|
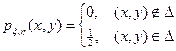
Событие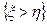 
соответствует множеству 
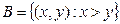на плоскости, т.е. полуплоскости. Тогда вероятность
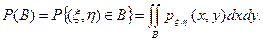
На полуплоскости B совместная плотность 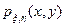равна нулю вне множества 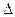и ½ внутри множества 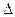. Таким образом, полуплоскость B разбивается на два множества 
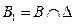и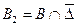 
. Следовательно, двойной интеграл по множеству B представляется в виде суммы интегралов по множествам 
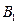и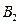 
, причем второй интеграл равен нулю, так как там совместная плотность равна нулю. Поэтому
.
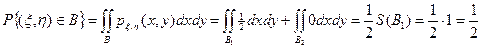Если задана совместная плотность распределения 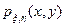для пары (x, h), то плотност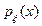и 
и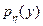 
составляющих x и h называются частными плотностями и вычисляются по формулам:
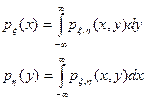
Случайные величины x, h называются независимыми, если при любых х и у независимыми являются события {x<х} и {h<у}, т.е.
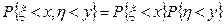
Для непрерывно распределенных случайных величин с плотностями рx(х), рh(у) независимость означает, что
.
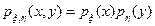Задача 6.В условиях предыдущей задачи определить, независимы ли составляющие случайного вектора x и h?
Решение. Вычислим частные плотност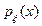и и 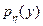. Имеем:
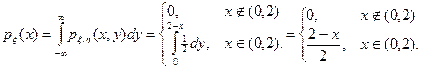
Аналогично,
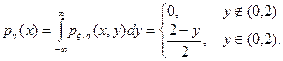
Очевидно, что в нашем случае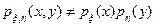 
, и потому случайные величины x и h зависимы.
|
|
|
Числовые характеристики для случайного вектора (x, h) можно вычислять с помощью следующей общей формулы. Пусть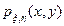 
— совместная плотность величин x и h, а j(х, у) — функция двух аргументов, тогда
.
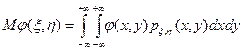В частности,
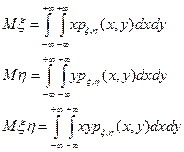
Задача 7. В условиях предыдущей задачи вычислить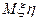 
.
Решение. Согласно указанной выше формуле имеем:
.
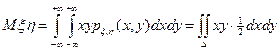Представив треугольник 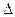в виде
,
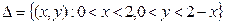двойной интеграл можно вычислить как повторный:
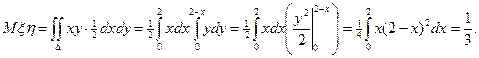
Дата добавления: 2021-03-18; просмотров: 127; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!