Системы линейных алгебраических уравнений (СЛАУ).
Определение 2.14 . Системой линейных уравнений (линейной системой) называется система вида
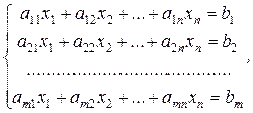 (2.6)
(2.6)
где 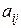 ,
, 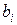 - числа,
- числа, 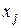 - неизвестные, n – число неизвестных, m – число уравнений.
- неизвестные, n – число неизвестных, m – число уравнений.
Определение 2.15. Решением линейной системы (2.6) называется набор чисел 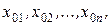 которые при подстановке вместо неизвестных обращают каждое уравнение системы в тождество.
которые при подстановке вместо неизвестных обращают каждое уравнение системы в тождество.
Определение 2.16. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
Определение 2.17. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
Определение 2.18. Для системы линейных уравнений вида (2.6) матрица
А = 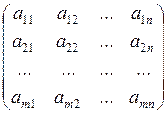 называется матрицей системы, а матрица
называется матрицей системы, а матрица
А*= 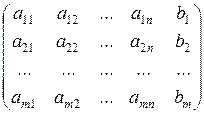 называется расширенной матрицей системы
называется расширенной матрицей системы
Терема Кронекера – Капелли (критерий совместимости системы)
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Определение 2.19. Если b1, b2, …,bm = 0, то система называется однородной. Однородная система всегда совместна.
Матричный метод решения систем линейных уравнений.
Пусть дана система уравнений: (2.6)
Составим матрицы: A =  ; B =
; B = 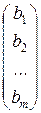 ; X =
; X = 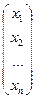 .
.
Тогда систему уравнений (2.6) можно записать в матричной форме:
A × X = B. (2.7)
Рассмотрим частный случай системы (2.6), когда число уравнений равно числу неизвестных, т.е. m = n. Пусть квадратная матрица А является невырожденной, т.е. существует обратная матрица А-1 . Умножим обе части уравнения (2.7) слева на А-1, получим решение системы (2.6, m = n) в матричной форме
X = A -1 B. (2.8)
Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.
Метод Крамера.
Другой метод решения системы линейных алгебраических уравнений основан на теореме Крамера.
Система из n уравнений с n неизвестными
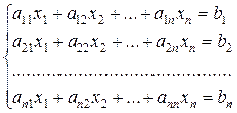 (2.9)
(2.9)
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = D i / D , (2.10)
где D = det A , а D i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi .
D i = 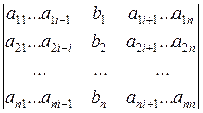 .
.
Формулы вычисления неизвестных (2.8) носят название формул Крамера. Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:
1) Если 
 система (2.3) имеет единственное решение, определяемое по формулам:
система (2.3) имеет единственное решение, определяемое по формулам: 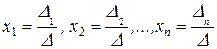 .
.
2) Если  =
= 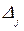 = 0, система имеет бесконечно много решений.
= 0, система имеет бесконечно много решений.
3) Если  = 0, а хотя бы один из
= 0, а хотя бы один из 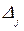
 система не имеет решений.
система не имеет решений.
Если система однородна, т.е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.
Пример. Найти решение системы уравнений: 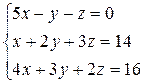
D = 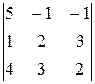 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = 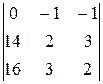 = (28 – 48) – (42 – 32) = -20 – 10 = -30. x1 = D1/D = 1;
= (28 – 48) – (42 – 32) = -20 – 10 = -30. x1 = D1/D = 1;
D2 = 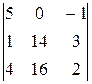 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2 = D2/D = 2;
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2 = D2/D = 2;
D3 = 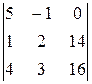 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = D3/D = 3.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = D3/D = 3.
Метод Гаусса
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:

Разделим обе части 1–го уравнения на a11 ¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения
и т.д.
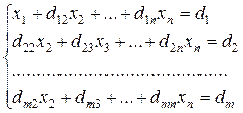 , где d1j = a1j/a11, j = 2, 3, …, n+1.
, где d1j = a1j/a11, j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Пример. Решить систему линейных уравнений методом Гаусса.
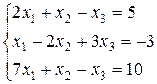
Составим расширенную матрицу системы.
А* = 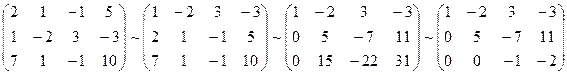
Таким образом, исходная система может быть представлена в виде:
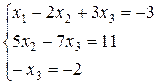 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
Дата добавления: 2021-03-18; просмотров: 69; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
