Примеры для самостоятельного решения
Основы линейной алгебры
Одной из основных задач линейной алгебры является решение систем линейных алгебраических уравнений. К таким системам сводятся многие задачи математического моделирования физических и технологических процессов при их дискретизации, т.е. представления соответствующих дифференциальных уравнений через конечные разности или конечные элементы. Используя алгебру матриц, система линейных алгебраических уравнений представляется в наиболее простой и компактной форме
А X = B, (2.1)
где А – матрица коэффициентов системы уравнений (основная матрица), X – матрица-столбец неизвестных, В – матрица-столбец свободных членов. Поэтому удобно проводить исследование решений системы (2.1), используя язык матриц. Рассмотрим элементы алгебры матриц.
Понятие матрицы
Определение 2.1. Матрицейназывается прямоугольная таблица из n × m чисел, которая содержит m строк и n столбцов.
Обозначения : 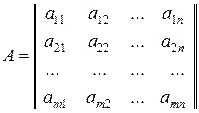 или
или 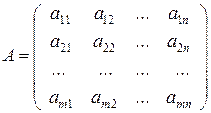 . (2.2)
. (2.2)
Либо кратко [а ij ] ( i = 1,2,…,n ; j = 1,2,..,m ). В этом случае имеется в виду, что матрица имеет размерность n × m . Матрицы обозначают заглавными латинскими буквами А , В , С, Е, ... Числа aij называются элементамиматрицы, где первый индекс i означает номер строки, а второй j - номер столбца.
Если в квадратной матрице все элементы главной диагонали равны единице, а все остальные равны нулю, то её называют единичной матрицей.Она обозначается буквой Е и имеет вид
|
|
|
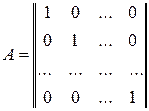 . (2.3)
. (2.3)
Определение 2.2. Две матрицы А и В называются равными, если они имеют одинаковое количество строк и столбцов и соответствующие элементы которых совпадают.
Матрица, в которой все элементы равны нулю, называется нуль-матрицей или нулевой. Её обозначают буквой О.
Если матрица состоит только из одной строки, то она называется матрицей-строкой. Матрица, состоящая из одного столбца называется матрицей-столбцом.
Если в матрице А поменять строки на столбцы, а столбцы – на соот-ветствующие строки, то полученную матрицу называют транспонированнойи обозначают А T .
Действия над матрицами
Сложение.
Операция сложения матриц вводится только для матриц одинаковых размеров.
Определение 2.3. Суммой двух матриц 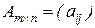 и
и  называется матрица
называется матрица 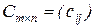 такая, что
такая, что  .
.
Пример
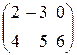 +
+  =
= 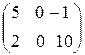 .
.
Аналогично определяется разность матриц .
Умножение на число
Определение 2.4. Произведеним матрицы 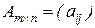 на число k называется матрица
на число k называется матрица  такая, что
такая, что 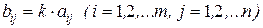
|
|
|
Пример
А = 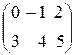 , k = 2, A ∙ k =
, k = 2, A ∙ k = 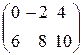 .
.
Разность матриц А – В можно определить так: А – В = А +(– В).
Операции сложения и умножения матрицы на число обладают следующими свойствами:
1. А + В = В + А; 5. 1 ∙ А =А;
2. А + (В + С) = (А + В) + С; 6. α ∙(А + В)= α ∙А + α ∙В;
3. А + О = А ; 7. (α + β)∙А = α ∙А + β ∙А;
4. А – А = О; 8. α ∙ ( β ∙ А) = (α ∙ β) ∙ А ,
где А, В, С – матрицы, α, β – числа.
Произведение матриц.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Определение 2.5. Произведением матрицы 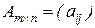 на матрицу
на матрицу 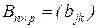 называется матрица
называется матрица 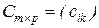 такая, что
такая, что
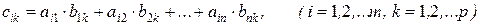 ,
,
т.е. элемент i-ой строки и k го столбца матрицы произведения С равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Получение элемента  схематично изображается так:
схематично изображается так:

Если матрицы А и В квадратные одного размера, то произведение А∙В и В∙А всегда существуют. Легко показать, что А∙Е = Е∙А=А , где А – квадратная матрица, Е – единичная матрица того же размера.
Пример
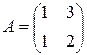 ,
, 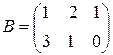 . Тогда произведение матриц А
. Тогда произведение матриц А  В определяется следующим образом:
В определяется следующим образом:
|
|
|
А 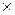 В =
В =  ∙
∙ 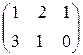 =
=  =
= 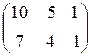 .
.
При этом произведение В 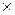 А не определено, так как число столбцов матрицы В(3) не совпадет с числом строк матрицы А(2).
А не определено, так как число столбцов матрицы В(3) не совпадет с числом строк матрицы А(2).
Матрицы А и В называются перестановочными, если АВ = ВА.
Умножение матриц обладает следующими свойствами
1. А ∙ (В ∙ С)= (А ∙ В) ∙ С; 3. (А + В) ∙ С = А∙С + В∙С ;
2. А ∙ (В + С) = А∙В + А∙С ; 4. α ∙ (А ∙ В)= (α∙А) ∙ В ,
если, конечно, написанные суммы и произведения матриц имеют смысл.
Для операции транспонирования верны свойства:
1. (А+В)Т = АТ + ВТ; 2. (А∙В)Т = АТ ∙ ВТ.
Определители
Любой квадратной матрице А порядка n ставится в соответствие некоторое число, называемое определителем этой матрицы.
Обозначение: det A (или | A | или ΔA ).
Определение 2.6. Определителем матрицы 1–го порядка (т.е. матрицы, состоящей из одного элемента, одного числа) называется само число, составляющее заданную матрицу.
Определение 2.7. Определителем матрицы 2-го порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
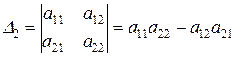 .
.
Определение 2.8. Определитель третьего порядка вычисляется по формуле:
|
|
|

При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников, которое символически можно представить так:
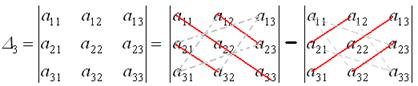
Примеры. Вычислить определители третьего порядка
1. 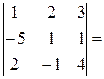
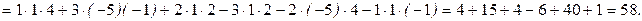
2. 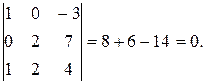
Для вычисления определителя матриц 4-го и более высоких порядков рассмотрим дополнительные понятия. Рассмотрим определитель матрицы А n -го порядка
Δn = 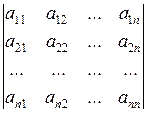 .
.
Определение 2.9. Выделим в нём какой-либо элемент aij и вычеркнем i-ю строку и j-й столбец, на пересечении которых расположен этот элемент. Полученный определитель ( n -1)–го порядка называется минором Mij элемента aij определителя Δn .
Определение 2.10. Наибольший порядок миноров матрицы А, отличных от нуля, называется рангом матрицы.
Определение 2.11. Алгебраическим дополнением элемента aij определителя Δn называется число
Aij = (-1)i+j Mij .
Определение 2.12. Определителем n -го порядка Δn вычисляетсясуммой произведения элементов любой строки (столбца)на их алгебраические дополнения
Δn = 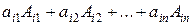 =
= 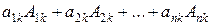 , 1 ≤ i , k ≤ n . (2.4)
, 1 ≤ i , k ≤ n . (2.4)
Пример. Вычислим определитель 4-го порядка 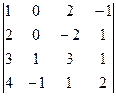 с помощью разложения по 2-му столбцу. Для этого найдем
с помощью разложения по 2-му столбцу. Для этого найдем 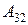 и
и 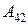 :
:
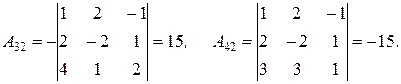
Следовательно, 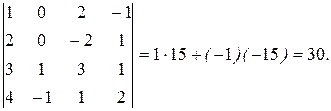
Квадратная матрица А называется невырожденной, если определитель Δ = det A ≠ 0. В противном случае (Δ = 0) матрица А называется вырожденной.
Определение 2.13. Матрица А-1 называется обратной матрице А, если выполняется условие
А А-1 = А-1 А = Е , (2.5)
где Е – единичная матрица того же порядка, что и матрица А. Отметим, что для вырожденной матрицы обратная матрица не существует.
Основные свойства определителей.
1. Определитель, имеющий нулевую строку (столбец), равен нулю.
2. При перестановке двух строк (столбцов) определитель меняет знак.
3. Определитель, имеющий две одинаковы строки (одинаковые столбцы),
равен нулю.
4. Общий множитель любой строки (столбца) можно вынести за знак оп-
ределителя.
5. Если каждый элемент некоторой строки (столбца) определителя Δn представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей. Поясним это на примере определителя 3-го порядка

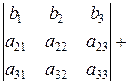
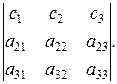
6. Величина определителя не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
7. При транспонировании матрицы её определитель не меняется.
Примеры для самостоятельного решения
Вычислить определители
1)  . 2)
. 2) 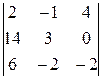 . 3)
. 3)  .
.
4) 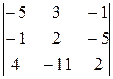 . 5)
. 5)  . 6)
. 6)  .
.
Дата добавления: 2021-03-18; просмотров: 76; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
