Экстремум функции двух переменных (максимум и минимум)
Лекция № 2 «Функции нескольких переменных»
Производная по направлению. Градиент функции
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 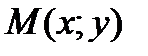 , l – некоторое направление, задаваемое единичным вектором
, l – некоторое направление, задаваемое единичным вектором  , где
, где  - направляющие косинусы вектора
- направляющие косинусы вектора 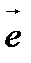 .
.
При перемещении в данном направлении l точки 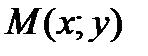 в точку
в точку 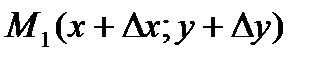 функция
функция  получит приращение
получит приращение  называемое приращением функции в направлении l .
называемое приращением функции в направлении l .
Опр. 1. Производной функции  по направлению l называется предел отношения приращения функции в этом направлении к величине перемещения
по направлению l называется предел отношения приращения функции в этом направлении к величине перемещения 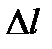 при стремлении последней к нулю, т.е.
при стремлении последней к нулю, т.е. 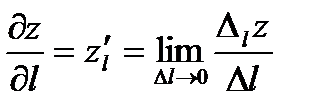 .
.
Производная 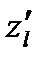 характеризует скорость изменения функции в направлении l. Рассмотренные ранее частные производные
характеризует скорость изменения функции в направлении l. Рассмотренные ранее частные производные 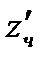 и
и 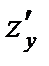 представляют собой производные по направлениям, параллельным соответственно осям Ох и Оу.
представляют собой производные по направлениям, параллельным соответственно осям Ох и Оу.
Примем без доказательства формулу для нахождения производно по направлению  (5).
(5).
При вычислении производной по направлению полезны формулы
 .
.
Пример1. Вычислить производную функции 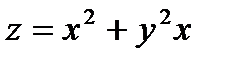 в точке
в точке  по направлению вектора
по направлению вектора  где
где 
Решение. Найдем координаты вектора  и его направляющие косинусы.
и его направляющие косинусы.

Находим частные производные функции их значения в точке М(1; 2)

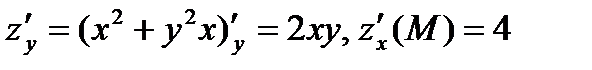
Применяем формулу (5) 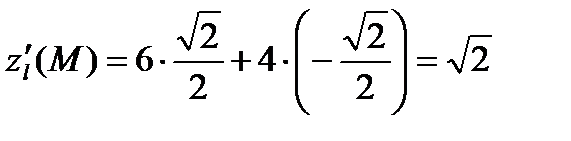
Опр. 2. Градиентом функции  называется вектор с координатами
называется вектор с координатами  .
.
Обозначают вектор градиента одним из следующих способов  .
.
Рассмотрим физический смысл вектора градиента. Найдем скалярное произведение вектора  и единичного вектора
и единичного вектора  направления l .
направления l .
|
|
|
Получим:  Сравнив полученное равенство с равенством (5) получим, что
Сравнив полученное равенство с равенством (5) получим, что 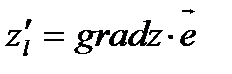 Известно, что скалярное произведение двух векторов максимально, если они одинаково направлены. Следовательно, градиент функции в данной точке характеризует направление максимальной скорости изменения функции в этой точке. Таким образом, из всех направлений на плоскости в данной точке в направлении вектора градиента функция растет быстрее всего и имеет место формула
Известно, что скалярное произведение двух векторов максимально, если они одинаково направлены. Следовательно, градиент функции в данной точке характеризует направление максимальной скорости изменения функции в этой точке. Таким образом, из всех направлений на плоскости в данной точке в направлении вектора градиента функция растет быстрее всего и имеет место формула

Пример 2. Найти градиент функции 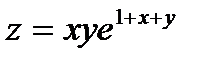 , его модуль и производную в направлении градиента в точке М(0; -1).
, его модуль и производную в направлении градиента в точке М(0; -1).
Решение. Находим частные производные функции и их значения в точке М.

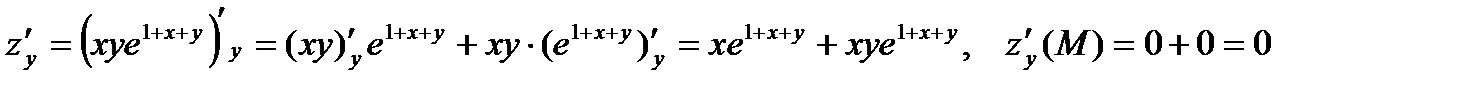
Тогда градиент функции равен 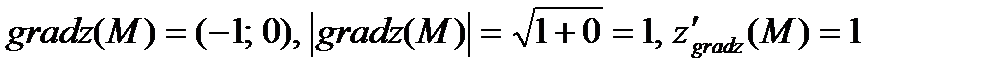 .
.
Касательная плоскость и нормаль к поверхности
Пусть функция  дифференцируема в некоторой области D, точка
дифференцируема в некоторой области D, точка 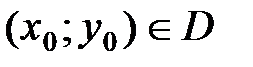 .
.
| x |
| y |
| z |
| x0 |
| y0 |
| M0 |
| O |
| b |
| a |
| Рисунок 1 |
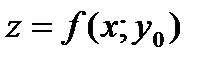
|
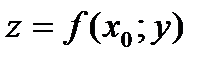
|
Пересечем поверхность S, изображающую функцию. плоскостями  Плоскости пресекают поверхность S по линиям
Плоскости пресекают поверхность S по линиям 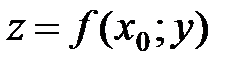 и
и 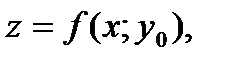 к каждой из которых в силу дифференцируемости функции в точке
к каждой из которых в силу дифференцируемости функции в точке 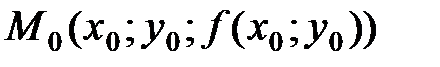 можно провести касательные l 1 и l 2 (рис. 1)
можно провести касательные l 1 и l 2 (рис. 1)
Прямые l 1 и l 2 определяют плоскость 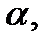 которая называется касательной плоскостью к поверхности S в точке М.
которая называется касательной плоскостью к поверхности S в точке М.
|
|
|
Получим уравнение этой плоскости. Так как плоскость проходит черед точку 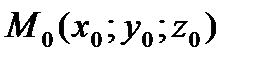 будем искать ее уравнение в виде
будем искать ее уравнение в виде 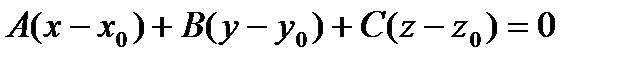 Преобразуем данное уравнение к виду
Преобразуем данное уравнение к виду 
Найдем коэффициент А1. Касательная l 2 лежит в плоскости 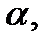 , следовательно, координаты точек касательной удовлетворяют уравнению плоскости, поэтому имеет место система уравнений
, следовательно, координаты точек касательной удовлетворяют уравнению плоскости, поэтому имеет место система уравнений 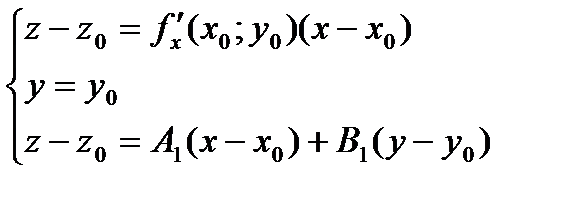 . Решая систему. получим
. Решая систему. получим 
Аналогично получим 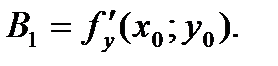
Подставим полученные выражения в уравнение касательной плоскости, тогда уравнение примет следующий вид:
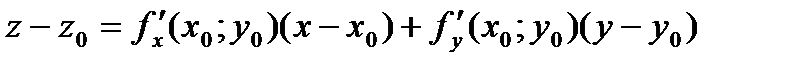 (6).
(6).
Прямая, проходящая через точку 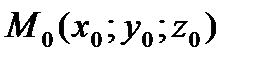 и перпендикулярная касательной плоскости, построенной к этой поверхности, называется нормалью.
и перпендикулярная касательной плоскости, построенной к этой поверхности, называется нормалью.
Уравнение нормали можно получить в каноническом виде, используя условие перпендикулярности прямой и плоскости (направляющий вектор прямой будет нормальным вектором для плоскости). Тогда уравнение нормали:
 (7)
(7)
Пример. Написать уравнение касательной плоскости и нормали к поверхности 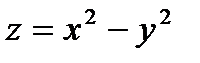 в точке
в точке 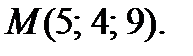
Решение. Найдем частные производные функции, их значения в точке М и воспользуемся уравнениями (6) и (7).


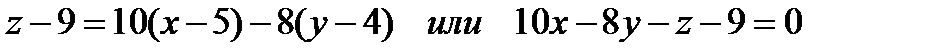
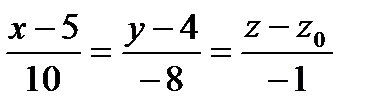
Экстремум функции двух переменных (максимум и минимум)
Пусть функция  определена в некоторой области D, точка
определена в некоторой области D, точка 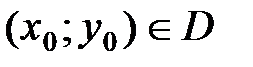 .
.
|
|
|
Опр. 1 Точка  называется точкой максимумафункции
называется точкой максимумафункции  , если существует такая d-окрестность точки
, если существует такая d-окрестность точки 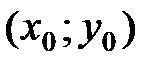 , что для каждой точки
, что для каждой точки 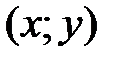 , отличной от точки
, отличной от точки 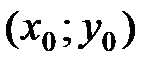 , из этой окрестности выполняется неравенство
, из этой окрестности выполняется неравенство 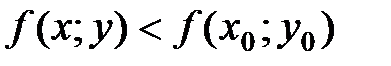 .
.
| · |
| · |
| · |
| · |
| · |
| · |
| · |
| · |
| · |
| x |
| z |
| y |
| N1 |
| N2 |
| f(x0;y0) f(x;y) |
| Рисунок 1 |
 называется точкой минимума функции
называется точкой минимума функции 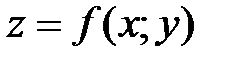 , если существует такая d-окрестность точки
, если существует такая d-окрестность точки  , что для каждой точки
, что для каждой точки  , отличной от точки
, отличной от точки 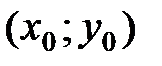 , из этой окрестности выполняется неравенство
, из этой окрестности выполняется неравенство 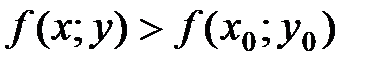 .
.
На рисунке 1:
N1 – точка минимума, а N2– точка максимума функции 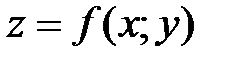 .
.
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции, или экстремумами функции.
На практике максимум и минимум функции находят с помощью необходимого и достаточного условий существования экстремума.
Дата добавления: 2021-02-10; просмотров: 54; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
