ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ
Задание 6
Производная функции
Введение
Математика - это наука, изучающая пространственные формы и количественные отношения действительного мира.
Математика играет важную роль в естественнонаучных, инженерно-технических и гуманитарных исследованиях. В то же время математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также элементом общей культуры. Поэтому основной задачей курса математики в образовательных заведениях среднего профессионального образования является обеспечение обучающихся математическими знаниями и умениями, необходимыми для изучения специальных дисциплин.
Тема «Производная. Применение производной функции» имеет огромное прикладное значение, в частности, при разработки курсовых, расчётно-графических работ и дипломных проектов, для профессиональной деятельности и продолжения образования.
ПРОИЗВОДНАЯ
Определение производной.
Пусть задана функция 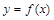 , определенная и непрерывная на некотором промежутке.
, определенная и непрерывная на некотором промежутке.
Предел отношения приращения функции в точке х0 к приращению аргумента, когда последний стремится к 0 называется производной функции:
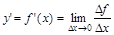 ,
,
 ,
, 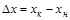
хк - конечное значение аргумента
хн - начальное значение аргумента
Механический и физический смысл производной
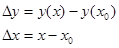
Пусть данная функция описывает движение материальной точки.
|
|
|
 Тогда
Тогда 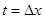 временной интервал
временной интервал
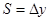 путь, пройденный точкой за данный промежуток времени
путь, пройденный точкой за данный промежуток времени  .
.
Определение. Скорость прямолинейногодвижения материальной точки в момент времени t есть производная пути S по времени t. В этом состоит механический смысл производной.
Т.е 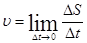 .
.
Обобщая можно сказать, что если функция 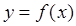 описывает какой - либо физический процесс, то производная
описывает какой - либо физический процесс, то производная 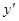 есть скорость протекания этого процесса. В этом состоит физический смысл производной.
есть скорость протекания этого процесса. В этом состоит физический смысл производной.
Физический смысл производной состоит в задаче нахождения мгновенной скорости движения:
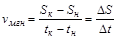 , пусть
, пусть 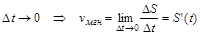 .
.
****************************************************************
1. Используя определение производной найдите 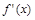 , если:
, если:
1)  ; 5)
; 5) 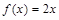 ;
;
2) 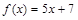 ; 6)
; 6) 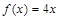 ;
;
3) 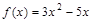 ; 7)
; 7) 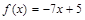 ;
;
4) 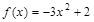 ; 8)
; 8) 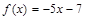 .
.
2. Точка движется по закону 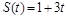 . Найти среднюю скорость движения за промежуток времени
. Найти среднюю скорость движения за промежуток времени
1) от 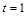 до
до 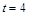 ; 2) от
; 2) от 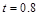 до
до 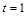 .
.
3. Найти мгновенную скорость движения точки, если
1) 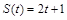 ; 2)
; 2) 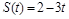 .
.
4. Закон движения задан формулой 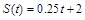 . Найти:
. Найти:
1) среднюю скорость движения от 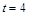 до
до 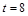 ;
;
2) скорость движения в момент 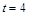 и
и 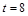 .
.
5. Определить скорость тела, движущегося по закону 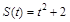 в момент времени
в момент времени 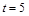 и
и 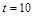 .
.
|
|
|
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ И ТАБЛИЦА ПРОИЗВОДНЫХ.
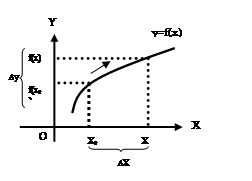
Геометрический смысл производной состоит в том, что тангенс угла наклона касательной к оси Ох называется производной функции в точке касания и равен угловому коэффициенту 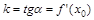 .
.
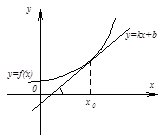
|
Уравнение касательной 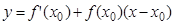
|
Таблица производных и правила дифференцирования:
1 правило. Производная суммы функций:  .
.
2 правило. Производная произведения функций: 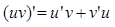 .
.
3 правило. Производная частного функций: 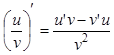 .
.
4 правило. Вынесение числового множителя за знак производной:  .
.
| Функция | Производная |
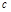
| 0 |

| 1 |
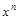
| 
|
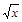
| 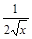
|
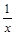
| 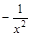
|

| k |
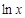
| 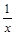
|
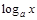
| 
|
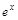
| 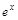
|
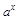
| 
|
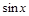
| 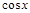
|
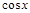
| 
|

| 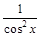
|
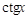
| 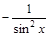
|
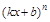
| 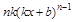
|
****************************************************************
1. Вычислить производные следующих функций:
1) 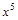 ; 20)
; 20) 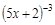 ; 39)
; 39) 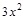 ;
;
2) 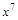 ; 21)
; 21) 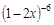 ; 40)
; 40) 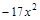 ;
;
3)  ; 22)
; 22) 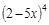 ; 41)
; 41) 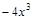 ;
;
4)  ; 23)
; 23)  ; 42)
; 42) 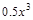 ;
;
5) 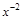 ; 24)
; 24) 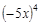 ; 43)
; 43) 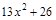 ;
;
6) 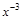 ; 25)
; 25) 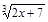 ; 44)
; 44)  ;
;
7)  ; 26)
; 26) 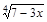 ; 45)
; 45) 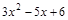 ;
;
8)  ; 27)
; 27) 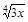 ; 46)
; 46)  ;
;
9) 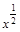 ; 28)
; 28) 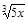 ; 47)
; 47)  ;
;
10) 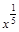 ; 29)
; 29) 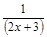 ; 48)
; 48) 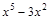 ;
;
|
|
|
11) 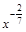 ; 30)
; 30)  ; 49)
; 49) 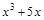 ;
;
12) 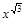 ; 31)
; 31) 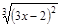 ; 50)
; 50)  ;
;
13) 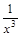 ; 32)
; 32) 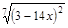 ; 51)
; 51) 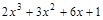 ;
;
14) 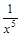 ; 33)
; 33) 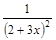 ; 52)
; 52) 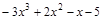 ;
;
15) 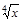 ; 34)
; 34)  ; 53)
; 53) 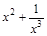 ;
;
16)  ; 35)
; 35) 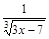 ; 54)
; 54) 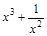 ;
;
17)  ; 36)
; 36) 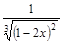 ; 55)
; 55) 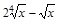 ;
;
18) 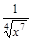 ; 37)
; 37) 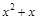 ; 56)
; 56) 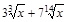 .
.
19) 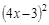 ; 38)
; 38) 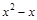 ;
;
2. Найдите 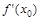 , если
, если
1) 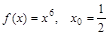 ; 2)
; 2) 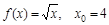 ;
;
3)  ; 9)
; 9) 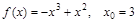 ;
;
4) 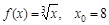 ; 10)
; 10)  ;
;
5) 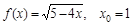 ; 11)
; 11) 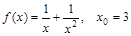 ;
;
6)  ; 12)
; 12) 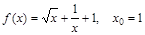 ;
;
7) 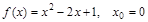 ; 13)
; 13) 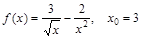 ;
;
8) 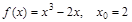 ; 14)
; 14) 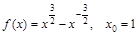 .
.
3. Найдите значения х, при которых значение производной равно 0, если:
1)  ; 5)
; 5) 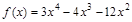 ;
;
2) 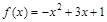 ; 6)
; 6) 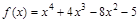 ;
;
3) 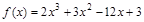 ; 7)
; 7) 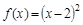 .
.
4) 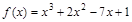 ;
;
4. Выяснить при каких значениях х производная принимает положительные и отрицательные значения, если:
1) 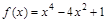 ; 5)
; 5)  ;
;
2)  ; 6)
; 6)  ;
;
3)  ; 7)
; 7) 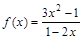 ;
;
4)  ; 8)
; 8)  .
.
5. Найти производные следующих функций:
1)  ; 7)
; 7) 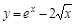 ;
;
2) 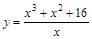 ; 8)
; 8) 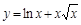 ;
;
3) 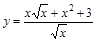 ; 9)
; 9) 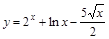 ;
;
4)  ; 10)
; 10) 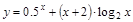 ;
;
5) 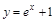 ; 11)
; 11)  ;
;
6)  ; 12)
; 12) 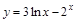 ;
;
13) 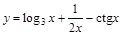 ; 18)
; 18) 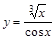 ;
;
14) 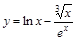 ; 19)
; 19)  ;
;
15) 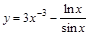 ; 20)
; 20)  ;
;
16) 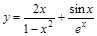 ; 21)
; 21) 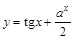 .
.
17)  ;
;
6. Найдите угловой коэффициент касательной к графику функции 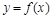 в точке с абсциссой
в точке с абсциссой  :
:
|
|
|
1) 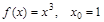 ; 3)
; 3) 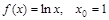 ;
;
2)  ; 4)
; 4) 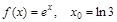 .
.
7. Написать уравнение касательной к графику функции 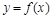 в точке с абсциссой
в точке с абсциссой  :
:
1) 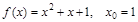 ; 5)
; 5)  ;
;
2) 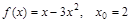 ; 6)
; 6) 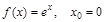 ;
;
3) 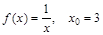 ; 7)
; 7) 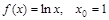 ;
;
4)  ; 8)
; 8) 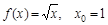 .
.
8. Найти угол между касательной к графику функции 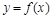 в точке с абсциссой
в точке с абсциссой  и осью Ох:
и осью Ох:
1) 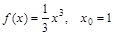 ; 4)
; 4) 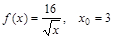 ;
;
2) 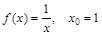 ; 5)
; 5) 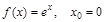 ;
;
3)  ; 6)
; 6) 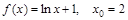 .
.
9. Написать уравнение касательной к графику функции 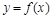 в точке с абсциссой
в точке с абсциссой 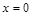 :
:
1) 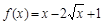 ; 3)
; 3) 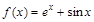 ;
;
2)  ; 4)
; 4) 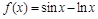 .
.
Проверь себя!
1. Найти  , если
, если 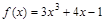 .
.
2. Найти производную функции:
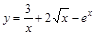 ;
;  ;
;
 ;
; 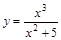 .
.
3. Найти угловой коэффициент касательной к графику функции  в точке с абсциссой
в точке с абсциссой 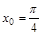 .
.
4. Найти угол между касательной к графику функции  в точке с абсциссой
в точке с абсциссой 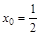 и осью Ох.
и осью Ох.
Сложная функция.
Сложная функция – это функция от функции:  .
.
Производную сложной функции считают с помощью правила цепочки, которое состоит в следующем: производная сложной функции равна произведению производных входящих в нее функций:
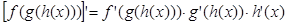 .
.
****************************************************************
1. Найти производные следующих функций:
1) 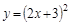 ; 8)
; 8)  ;
;
2) 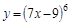 ; 9)
; 9)  ;
;
3) 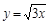 ; 10)
; 10) 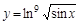 ;
;
4)  ; 11)
; 11) 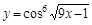 ;
;
5) 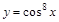 ; 12)
; 12) 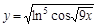 ;
;
6) 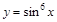 ; 13)
; 13) 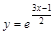 ;
;
7)  ; 14)
; 14) 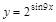 .
.
2. Найти значения х, при которых значение производной функции 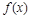 равно 0; положительно; отрицательно:
равно 0; положительно; отрицательно:
1) 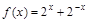 ; 4)
; 4) 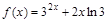 ;
;
2) 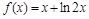 ; 5)
; 5) 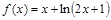 ;
;
3) 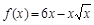 ; 6)
; 6)  .
.
3. Написать уравнение касательной к графику функции в точке с абсциссой  , если:
, если:
1)  ; 3)
; 3) 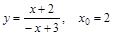 ;
;
2) 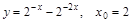 ; 4)
; 4) 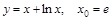 .
.
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ
Нахождение стационарных точек и промежутков монотонности.
Достаточный признак убывания (возрастания) функции, теорема Лагранжа, понятия «промежутки монотонности функции»
Экстремумы функции и значения в них
Определения точек максимума и минимума, необходимый признак экстремума (теорему Ферма) и достаточный признак максимума и минимума, знать определения стационарных и критических точек функции
Исследование и построение графиков функций.
Схема исследования функции, метод построения графика чётной (нечётной) функции
Нахождение наибольших и наименьших значений функций.
Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке и на интервале
Дата добавления: 2021-02-10; просмотров: 57; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
