Краткий анализ основ геометрий 26 страница

Неявное существование в русском ряду чисел-отрезков, способных образовывать прямоугольные треугольники, не может быть случайностью. Похоже, что они выполняют какую-то неизвестную нам функцию, определяемую степенями и последовательностью чисел.

Но можно представить и другую картину. Имеются два ортогональных бесконечных катета, пересекаемых на пропорциональном иррациональном расстоянии параллельными линиями, отрезки которых превращаются в гипотенузы. А это уже не цепочка, а плоскость. И сразу же возникает предположение, что прямоугольные треугольники есть элементы прямоугольников, а их катеты - стороны прямоугольников. Продолжение катетов - оси координат х и у на плоскости, а гипотенузы - диагонали образовавшихся прямоугольников. И прорисовывающаяся естественным образом координатная сетка начинает походить на истоки некоей новой геометрии. Посмотрим, что еще скрывается в этом ряду.

Вернемся к теореме Пифагора об образующей плоскости и построим ее объемный аналог в трехмерном евклидовом пространстве. Проиндексируем любую последовательность из четырех чисел русского ряда, исходя из того, что каждые три числа последовательности образуют прямоугольник с двумя сторонами и диагональю: х, у, l, n, где l и n - диагонали прямоугольников x, y, l и y_o, l, n. Они образуют следующие пропорции:

x² + y² = l² ,

y_o² +l² = n².

Здесь у по количественной величине равно у_о, но ортогонально ему и х, а потому не складывается с у. Но, будучи ортогональной, плоскости ху,  у_о приобретает качество третьей координаты - z, и потому, приравняв z = у_о, получаем плоскостной аналог теоремы Пифагора для «трехмерного» пространства:

 x² + y² + z² = n².                                        (3.9)

Перед нами достаточно странное уравнение (3.9). Числа одного математического ряда своей взаимосвязью демонстрируют изменяемую по длине пространственную (объемную?) структуру (струну?), у которой поперечное сечение тоже изменяемая, но равная по высоте и ширине, скрытая за индексацией величина.

В отличие от общепринятой системы координат, индексация которой может содержать произвольный набор чисел, уравнение (3.9) составляется только из четырех иррациональных взаимосвязанных последовательных чисел русского ряда и по своему характеру является квантованной системой, т.е. качественно новым математическим образованием. Возникает вопрос: Случайно ли получается квантованная координатная система? Или она может послужить основанием для построения квантованной геометрии? Для ответа на этот вопрос продолжим преобразования уравнения (3.9). Перенесем все ее индексы в правую часть и получим запись одинаковую по форме, как для динамической, так и для статической геометрии:

0 = n² - x² - y² - z².                                            (3.10)

Рассматривая уравнение статической геометрии (3.10) Гильберт и Клейн предположили, что если приравнять n² = 1², то может существовать геометрия, в которой (3.10) имеет следующий вид:

0 ¹ 1² - x² - y² - z².                                 (3.10¢)

Поскольку правая часть уравнения не равна 0, то вместо 0 можно поставить s², и уравнение принимает вид:

s² = 1² - x² - y² - z²                                         (3.11)

Геометрия с таким основанием была названа псевдоевклидовой геометрией. Ее и использовал Минковский для введения «четвертого» измерения - времени t посредством приравнивания 1² = c²t²:

s² = c² t² - x² - y² - z².                                  (3.12)

И это уравнение (3.12), отображающее не четырехмерный объем, а «рассечение» трехмерного пространства пятью плоскостями утвердилось в науке под названием «четырехмерный мир Минковского». Однако ни уравнение (3.11) ни (3.12) не являются аналогами уравнений динамической геометрии (3.9) и (3.10), поскольку в них за координатной индексацией могут скрываться любые комбинации не связанных между собой чисел как рациональных, так и иррациональных (Например, квадрат произведения времени на скорость никак не связан с квадратами координатных осей.) А уравнения (3.9) и (3.10) образуются только иррациональными числами любых трех последовательных чисел русского ряда. Ни s ни n в данное уравнение, по-видимому, ввести невозможно, поскольку другие члены ряда не образуют соответствующих пропорций. Для осуществления подстановки n в (3.10) таким образом, чтобы получилось равенство вида n² = 1² - s², необходимо «выйти» за пределы русского ряда во вне. Необходимо отыскать матрицу, содержащую поле взаимосвязанных иррациональных чисел, включающее в свою структуру русский ряд. И такая матрица была найдена еще до рассмотрения данного ряда. Это русская матрица [2, 31].О русской матрице речь пойдет в последней главе, здесь же продолжим рассмотрение других особенностей деления отрезка в крайнем и среднем отношении.

3.3. Поэлементное деление отрезка

в крайнем и среднем отношении

 

Отметим еще раз: задача деления отрезка в крайнем и среднем отношении, рассмотренная в предыдущем разделе, может решаться двумя качественно различными способами: геометрическим и алгебраическим. Причем переход от одного способа к другому может явно не фиксироваться и в результате какое-то качество либо теряется (при переходе от геометрической формы к алгебраической) либо добавляется (переход от алгебраической к геометрической форме), что не отражается на количественных величинах, но изменяет понятийный смысл полученных результатов. Поэтому в процессе решения необходимо отслеживать каждую операцию, во избежание ошибок, обусловленных процессом перехода от одного метода к другому. Это изменение можно наглядно проследить на широко известном примере деления отрезка в крайнем и среднем отношении. Рассмотрим процедуру деления отрезка поэлементно.

Дан отрезок АС (повторим рис. 42), следовательно, он имеет определенную длину, допустим, в см. и скрытое за длиной качество определенной отдельности – отрезок, и это его качество не может исчезнуть в процессе проведения геометрического решения, но после разделения может оказаться другим.

      А              В                         С

            а                с

Делим его на две части-доли АВ и ВС. После деления имеем только две доли отрезка АС (другие качества). Одна АВ = а см., другая ВС = с см. Теперь отрезок АС не существует. Он сохраняется только на бумаге и в нашей памяти. В натуре остались только две его доли-отдельности а и с, и появилось другое, отличное от отрезка, качество – доли (рис. 43):

а ®

с ®

Рис. 43                      

И именно с ними производятся все математические операции для получения золотой пропорции. Формализуем отношение отрезков в виде уравнения:

с/а = (а + с )/с,                                              (3.13)

Для решения (3.13) отношение модулей с / а приравнивается к b:

b = с/а, b = (с см/а см)                                          (3.14) 

Записав отношение (3.14) мы в неявной форме переходим от геометрического метода решения задачи к алгебраическому, поскольку размерность в (3.14) сокращается, и в результате решения находится безразмерностный коэффициент b. Подставляя (3.14) в (3.13) совершаем законный математический подлог, поскольку а и с имеют размерность, а b ею не обладает. И получаем чисто алгебраическое уравнение, не имеющее никакого отношения к геометрии и к пропорции (3.13):

b² – b – 1 = 0                                            (3.15) 

Решение уравнения (3.15) дает безразмерностную величину b, численно равную золотому числу Ф, но не причастную к делению отрезка в крайнем и среднем отношении. Оно может оказаться следствием отношения между любыми случайными числами, или входить в некую математическую последовательность, или в степенной ряд, определяемый уравнением подобный уравнению (3.15). Число b не делит отрезок на две части, а отмечает количественное отношение модулей образовавшихся долей. Оно – алгебраическое следствие получения в результате деления некоторых пропорциональных размерностных величин, совпадающее с золотым числом по модулю. Оно безразмерностно и потому не относится к (3.13). Только получение размерностных величин долей в (3.13), образующих в результате решения ту же величину пропорции, может свидетельствовать о его делении в золотом сечении.

Кажущаяся простота и элегантность «превращения» геометрического уравнения в алгебраическое скрывают подводный камень в виде размерностной или формальной двух – трех качественности геометрических параметров (свойств) и двухкачественности (отдельность) безразмерностных элементарных алгебраических символов и знаков. Преобразование геометрического уравнения в алгебраическое сопровождается потерей качественности геометрических параметров и «отчуждением» всего уравнения от геометрии. Обратное «возвращение» уравнения из алгебры в геометрию возможно только с приданием алгебраическим знакам и символам качеств, присущих параметрам данного геометрического уравнения и в таком количестве и признаке, которое содержало первородное уравнение. Только в этом случае операция преобразования геометрического уравнения в алгебраическое и обратно может оставаться логически корректной.

Поскольку b не имеет отношения к делению отрезка и не имеет размерности, его невозможно подставить в (3.13), и с помощью b из (3.15) мы не можем отыскать количественную величину долей-отрезков. Однако, получив величину b, мы успокаиваемся, так и не выяснив, а каковы же длины долей а и с. А ведь геометрический смысл деления отрезка и заключался в попытке сначала выяснить длину долей, а уже потом определять их отношение. И если б мы заранее не знали, что Ф золотое число и не искали бы именно его безразмерностную величину посредством деления отрезка, то не обратили бы на результат никакого внимания. Значит решение уравнения (3.15) не дает нам геометрического ответа на поставленный вопрос.

Для решения задачи и получения размерностного золотого числа надо найти геометрическую формализацию уравнения (3.13). Это можно сделать, перемножив числители на знаменатели, и убрав последние, решить полученное уравнение:

a² + ас = c².                                                  (3.16) 

Заменив в уравнении (3.16) ас на b²:

b² = ас,                                                          (3.17) 

и подставив имеющий геометрический смысл b², (b² – см×см) в (3.16) получаем:

a² + b² = c²,                                                   (3.18) 

Итак, из (3.13) «найдено» уравнение Пифагора для прямоугольного треугольника. Хотя в геометрии оно трактуется как сумма площадей квадратов, построенных на катетах прямоугольного треугольника, его можно понимать и как сумму соотношения качеств долей а, b, и с в виде:

а²(см×см) + b²(см×см) = c²(см×см),                            (3.19) 

не нарушая, таким образом, геометричности уравнения и не сокращая размерностей. Появление в (3.18) новой геометрической величины b, как бы не имеющей отношения к АС, свидетельствует о том, что к одной из долей бывшего отрезка виртуально “примыкает” еще одна доля, о которой мы ничего не ведали, но о которой “помнят” образовавшиеся в результате деления доли (память числа, память формы [26]).

В результате доли исчезнувшего отрезка, разделенного надвое, образовали виртуальный прямоугольный треугольник (рис. 44). И в 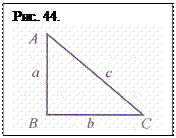него, в качестве одной из сторон, входит безразмерностная численная величина b, полученная из решения (3.15), равная по модулю золотому числу, приобретая в (3.19) размерность как сторона прямоугольного треугольника. Таким образом деление отрезка в крайнем и среднем отношении на две части - доли геометрическим методом приводит к появлению третьего отрезка – доли, равного по модулю золотому числу Ф, и образование ими прямоугольного треугольника. Совместное решение уравнений (3.13) и (3.18) (приведенное выше) дает численные величины долей-сторон треугольника а = 1,272…см, b = 1,618… см, с = 2,058… см, модули которых следующим образом соотносятся между собой: а³ = b² = с¹. И, следовательно, являются золотыми числами, а образованный ими треугольник – золотым треугольником. Только в этом случае величина b как размерностная сторона треугольника и равная по модулю золотому числу b = Ф, т.е. имеющая алгебраический и геометрический смысл в уравнениях (3.15) и (3.18), становится решением задачи о делении отрезка в крайнем и среднем отношении.

Задачу о делении отрезка в крайнем и среднем отношении иногда формализуют в «обобщенной форме»:

BC/AB = (AC/BC)^P,                                        (3.20) 

необоснованно, вводя в правую часть (3.20) в качестве степени целое неотрицательное число р, (р = 0, 1, 2, 3, … .) [30]. Пропорция (3.13) в виде (3.20) не может включать отрезка АС поскольку он, после разделения, отсутствует. Его же доли не могут геометрически складываться, они размерностные отдельности, и потому заменять (а + с) на АС логически некорректно, поскольку АC – одно качество, а доли – другие качества, несопоставимые и несовместимые с AC. Они всегда остаются отдельностями. Заменив в (3.20) из (3.13) суммы долей (а + с) на АС мы, с одной стороны, проводим математически некорректную операцию. С другой качественно меняем смысл уравнения, смешивая доли и отрезок. Это видно по такой записи уравнения (3.20):

ВС / АВ = (АС / ВС)^Р = (доля/доля)= (отрезок/доля)^Р (3.21)

И хотя каждый член уравнения (3.21) имеет одинаковую размерность, например в см, качественно они различны и по этой причине не могут корректно вводиться в одно уравнение. Геометрически в левой части уравнения (3.21) отдельности имеют одинаковое качество – длину, а правой части - различные качества – отрезок и доля отрезка, которые качественно не адекватны между собой и не могут, поэтому, быть членами одного уравнения. К тому же возводя, например, правую часть (3.20) в степень р, допустим, в квадрат, куб и т.д., мы получаем в левой части отношение долей, а в правой – отношение площадей кубов, и далее что-то геометрически бессмысленное, но никоим образом не отношение долей отрезка. Однако алгебраически в этом случае все корректно.

Само введение числа р устремленного от 1 ® ¥ неявно превращает геометрическое уравнение (3.13) в алгебраическое (3.20), поскольку неявно предполагает сокращение размерности в нем еще до начала решения. Но в постановке задачи не говорится о формализации и решении алгебраического уравнения, а только о геометрическом делении в крайнем и среднем отношении, что заранее обусловливает наличие размерности в уравнении деления. Поэтому привлечение целого неотрицательного числа р есть необоснованное изменение условия задачи, вызванное не геометрическими, а алгебраическими соображениями, поскольку в геометрии степенное изменение размерностной величины (отрезка) означает изменение его качественного содержания: квадрат отрезка – площадь, куб отрезка – объем, а далее в геометрии Евклида нет фигур со степенью > 3. Поэтому все дальнейшие рассуждения и решения (3.20) не имеют отношения к золотому сечению. Как полагают, преобразованное уравнения (3.20) с р = 1, 2, 3, …, n позволяет получать бесчисленное множество вариантов деления отрезка в «золотой пропорции». Вот как разделяется отрезок при возрастании р от 0 до 3:

 

а) р = 0,  A               C                 B, t _o = 2,

 

b)   p = 1,   A                                                   B,t ₁=1,618,                             C

с) p = 2,    А           C                             B,t ₂=1,465

 

d) p = 3,   A    C                                      B,t ₃=1,380

Рис. 45.                

И получаемые результаты обобщаются по всем t как некие «золотые числа», получаемые посредством деления степенных (?) пропорций отрезков в крайнем и среднем отношении.

Покажем, что получаемые при решении (3.20) числа не имеют отношения к золотым пропорциям и не могут обусловливать получение “обобщенных золотых пропорций” [8,30].

Уравнение (3,20) тоже решается методом замены, но другого из ее членов, безразмерностным символом х: х = АС : ВС, при этом ВС : АВ = х^р, а отрезок АВ есть сумма двух долей АС + СВ. Далее геометрическая операция заменяется алгебраической: и получается “аналог” уравнения (3.15) но уже со степенями при неизвестных:

х^р+1 - х^р - 1 = 0.                                   (3.22) 

Алгебраическое уравнение (3.22), при обозначении через t _р положительных корней решения задает бесконечное число пропорций как бы деления отрезка АВ в отношении (3.20):

t _о = 2;t ₁ = 1,618…;t ₂ = 1,465…;t ₃ = 1,380…;t ₄ = 1,324, и т.д.  (3.23)

---

Дата добавления: 2021-02-10; просмотров: 351; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!