Симплекс-метод решения задачи линейного программирования
Коломенский институт (филиал)
федерального государственного бюджетного образовательного учреждения
высшего образования
«МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра автоматизации производства и информационных технологий
П.С. Романов
Методические указания по выполнению лабораторной работы
По дисциплине
«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ
В МАШИНОСТРОЕНИИ»
Решение технологических и производственных задач методами линейного программирования
Коломна – 2019
Содержание
| 1. | Введение ....................................................................................................................... | 2 |
| 2. | Постановка оптимизационных задач планирования производства, сводящихся к задаче линейного программирования………………………………………………….. | 2 |
| 2.1. | Линейное программирование как область математического моделирования........... | 2 |
| 2.2. | Симплекс-метод решения задачи линейного программирования............................... | 4 |
| 2.3. | Примеры постановки оптимизационных задач планирования производства………. | 5 |
| 2.4. | Методика применения Microsoft EXCEL для решения ЗЛП…………………………. | 8 |
| 2.5. | Методика применения программы «Решение и моделирование задач линейного программирования»……………………………………………………………………. | 16 |
| 3. | Задание для лабораторной работы............................................................................ | 19 |
| 4. | Структура отчета......................................................................................................... | 20 |
| 5. | Исходные данные........................................................................................................ | 21 |
| 6. | Литература................................................................................................................... | 22 |
Введение
|
|
|
Лабораторная работа выполняется на основе теоретических положений теории математического программирования на ПЭВМ с использованием табличного процессора Microsoft EXCEL, Microsoft WORD в среде Windows 9*/NT/2000/ХР и специальной программы «Задача линейного программирования», разработанная в [4]. Цель работы:
изучение ряда положений теории математического программирования;
применение методов линейного программирования для моделирования технологических и производственных задач;
получение умений и навыков:
в использовании методов математического моделирования для решения оптимизационных технологических и производственных задач, сводящихся к задаче линейного программирования, на ЭВМ;
в анализе полученных результатов.
2. Постановка оптимизационных задач планирования производства, сводящихся к
Задаче линейного программирования
Линейное программирование как область математического моделирования
|
|
|
Огромное число оптимизационных задач планирования сводятся к так называемой задаче линейного программирования (ЗЛП). Линейное программирование посвящено теории и методам решения экстремальных задач, характеризующихся линейной зависимостью между переменными [1…3]. Оно связано с нахождением наилучших вариантов при решении различных производственных задач. В этих задачах имеется большая свобода изменения различных параметров и ряд ограничивающих условий. Требуется найти такие значения параметров, которые (с определенной точки зрения) были бы наилучшими. К таким задачам относятся задачи нахождения наиболее рационального способа использования сырья и материалов, определения выгодных режимов выполнения технологических процессов (ТП), повышения эффективности работы межцехового и внутрицехового транспорта и др.
В самом общем виде задачу линейного программирования можно записать следующим образом: требуется найти оптимальные значения n переменных х1, х2, . . ., х n доставляющие экстремум (максимум (или минимум)) линейной целевой функции:
, (1)
при ограничениях
|
|
|
|
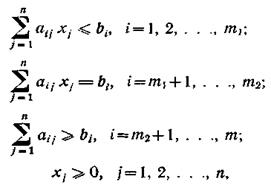
где cj (j=1,2,...,n), aij{i=1,2,...,m; j=1,2,...,n), bi (i=1,2,...,m) — заданные числа.
Отличительная особенность ЗЛП состоит в линейности всех функций, задающих целевое условие (целевой функции) (1), ограничений (2)-(5). Причем (5) – это условие неотрицательности всех переменных, что вытекает из реального технологического (экономического) смысла переменных. Ограничения вида (5) называют тривиальными.
Наиболее часто встречаются следующие две разновидности ЗЛП.
1. Каноническая ЗЛП. Для такой задачи система ограничений, помимо тривиальных ограничений (5), включает в себя только уравнения. Примером может служить транспортная задача.
2. Стандартная ЗЛП. В этом случае система ограничений состоит только из неравенств, в число которых входят и условие (5). Примером могут служить задачи планирования производства, например, объемное планирование работы механического участка для достижения максимальной загрузки технологического оборудования. Указанные разновидности сводятся одна к другой.
Различие этих разновидностей заключается только в том, что в одной задаче была дана система линейных неравенств, а в другой — система линейных уравнений. Неравенства легко преобразовать в уравнения (переход от канонической к стандартной ЗЛП и обратно). Следовательно, можно сделать так, что математически формулировки этих задач будут совершенно одинаковыми. Общая формулировка этих задач будет такой: дана система m независимых алгебраических уравнений с n>m неизвестными переменными (x1,х2, . . .,хn):
|
|
|
(6)
и линейная форма 
относительно этих неизвестных.
Требуется среди всех неотрицательных решений заданной системы (6) выбрать такое, при котором (1) принимает наибольшее (наименьшее) значение. Эта задача носит название основной задачи линейного программирования (ОЗЛП).
Допустимым решением ОЗЛП называют любую совокупность переменных x1 
0, x2 0,…,xn 0 удовлетворяющую уравнениям (6). Оптимальным решением называют то из допустимых решений, при котором (1) принимает максимальное (минимальное) значение. Если уравнения (6) противоречат друг другу, то ОЗЛП не имеет решения.
Характерной особенностью ЗЛП является то, что число уравнений меньше числа неизвестных, т.е. m<n.
Итак, суть ЗЛП состоит в том, чтобы из множества допустимых решений системы (6) выбрать только одно, которое обращает в минимум (или максимум) целевую функцию (1). При этом допустимым решением называют любое решение системы (6) с неотрицательными значениями переменных (xj≥0).
Чаще всего в задаче линейного программирования все или некоторые из уравнений имеют вид неравенства:
Однако такие неравенства можно легко превратить в уравнения, вводя дополнительные переменные хn+i так, чтобы в зависимости от знака неравенства имело место одно из двух выражений:
(7)
Решение системы уравнений (7), в которой число переменных n больше числа уравнений m, можно найти, если (n – m) каких-либо переменных положить равными нулю. Тогда полученную при этом систему m уравнений с n неизвестными можно решить обычными методами алгебры. Найденное при этом решение называют базисным. Базисом называют любой набор переменных m, таких, что определитель, составленный из коэффициентов при этих переменных, не равен нулю. Эти m переменных называют базисными переменными. Остальные (n – m) переменных называют свободными переменными. Если принять все свободные переменные равными нулю и решить полученную систему m уравнений с n неизвестными, то получим базисное решение.
Однако среди базисных решений будут такие, которые дадут отрицательные значения некоторых базисных переменных, что противоречит условию задачи (5), поэтому такие решения недопустимы.
В настоящее время разработаны рациональные способы перебора базисных решений, которые позволяют рассматривать не все допустимые базисные решения, а их минимальное число. Наиболее распространенными методами такого перебора являются так называемый симплекс-метод и табличный метод решения задачи линейного программирования. В лабораторной работе для решения задач используется симплекс-метод.
Симплекс-метод решения задачи линейного программирования
Суть симплекс-метода состоит в следующем:
1. Находят какое-либо допустимое базисное решение. Его можно найти, приняв какие-либо (n – m) переменных за свободные, приравняв их к нулю и решив получившуюся систему уравнений. Если при этом некоторые из базисных переменных окажутся отрицательными, то нужно выбрать другие свободные переменные, т.е. перейти к новому базису.
2. Проверяют, не достигнут ли уже максимум целевой функции при найденном допустимом базисном решении.
3. Если оптимальное решение не найдено, то ищут новое допустимое базисное решение, но не любое, а такое, которое увеличивает значение целевой функции. Проверку того, достигнут ли при найденном допустимом решении максимум целевой функции, можно сделать путем поиска нового базисного решения. Для перехода к новому базисному решению одну из свободных переменных следует сделать базисной, при этом она станет отличной от нуля, т.е. возрастет. Следовательно, если какая-либо из свободных переменных входит в выражение для целевой функции со знаком плюс и при ее увеличении целевая функция увеличивается, то максимум целевой функции не достигнут, и данную переменную следует превратить в базисную, сделав ее отличной от нуля. Однако при возрастании свободной переменной некоторые из базисных переменных будут уменьшаться. Поскольку отрицательные значения переменных недопустимы, то в качестве новой свободной переменной следует принять ту из базисных переменных, которая раньше других обращается в ноль.
Методика и примеры решения задачи линейного программирования симплекс-методом представлены в работах [1…4].
Рассмотрим постановки нескольких типовых оптимизационных задач.
2.3. Примеры постановки оптимизационных задач планирования производства
Задача 1. Объемное планирование работы механического участка для достижения максимальной загрузки технологического оборудования [5]
Имеется m-станков (или m-групп станков), на которых могут быть изготовлены n-типов деталей. Трудоемкость обработки j-ой детали на i-ом станке составляет tij, час (см. табл. 1), известны также фонды времени работы каждого станка (группы станков) – Bi.
Таблица 1
Исходные данные к задаче
| Станки | Трудоемкость при обработке деталей каждого типа | Фонд времени работы оборудования, час | |||
| 1 | 2 | … | n | ||
| 1 | t11 | t12 | … | t1n | B1 |
| 2 | t21 | t22 | … | t2n | B2 |
| … | … | … | … | … | … |
| m | tm1 | tm2 | … | tmn | Bm |
Требуется определить количество деталей каждого наименования (x1, x2, …, xn), при обработке которых достигается максимальная загрузка оборудования участка. Математически задача сводится к максимизации следующей ЦФ:
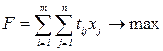, (8)
при ограничениях:
(9)
(10)
Задача 2. Планирование работы механического участка для достижения максимальной прибыли [5]
Для изготовления n видов изделий завод использует m видов сырья, запас каждого из которых ограничен Ri. Для изготовления изделий задействованы s видов оборудования, для которых ограничен фонд рабочего времени Bk. Также известна прибыль от реализации каждого изделия Mj. Исходные данные сведены в табл. 2. Требуется определить план выпуска продукции, при котором будет достигнута максимальная прибыль.
Если обозначить через xj – число изделий каждого из n видов выпускаемых изделий то, математически задача сведется к максимизации ЦФ:
, (11)
при ограничениях:
(12)
(13)
(14)
Таблица 2
Исходные данные к задаче
| Виды сырья | Потребность в сырье для изделий, кг | Ресурсы, кг | |||
| 1 | 2 | … | n | ||
| 1 | p11 | p12 | … | p1n | R1 |
| 2 | p21 | p22 | … | p2n | R2 |
| … | … | … | … | … | … |
| m | pm1 | pm2 | … | pmn | Rm |
| Оборудование | Время изготовления изделий, час | Фонд времени работы оборудования, час | |||
| 1 | 2 | … | n | ||
| 1 | t11 | t12 | … | t1n | B1 |
| 2 | t21 | t22 | … | t2n | B2 |
| … | … | … | … | … | … |
| s | ts1 | ts2 | … | tsn | Bs |
| Прибыль на одно изделие, усл. руб. | М1 | М2 | … | М n | |
Иногда, в таких задачах вводят дополнительные жесткие условия. Например, требуется, чтобы полностью был выработан фонд времени работы Bk одного вида оборудования. В этом случае, одно из ограничений (13) записывается в строгой форме:
. (15)
Задача 3. Задача о минимальной загрузке оборудования [5].
Имеется m станков, на которых могут быть обработаны n типов деталей. Производительность i-го станка при изготовлении j-ой детали составляет cij. Величины плановых заданий Aj на изготовление j-ой детали и ресурс времени работы Bi известны. Все исходные данные можно представить в виде табл.3. Требуется, учитывая ресурсы времени работы каждого станка, распределить задания между станками таким образом, чтобы общее время работы всех станков было минимальным.
Таблица 3
Исходные данные к задаче
| Станки | Производительность обработки детали каждого типа | Фонд времени работы оборудования, час | |||
| 1 | 2 | … | n | ||
| 1 | c11 | c12 | … | c1n | B1 |
| 2 | c21 | c22 | … | c2n | B2 |
| … | … | … | … | … | … |
| m | cm1 | cm2 | … | cmn | Bm |
| Требуемое количество деталей | A1 | A2 | … | An | |
Если обозначить tij – время изготовления j-ой детали на i-ом станке, то математически можно записать задачу минимизации ЦФ:
, (16)
при ограничениях:
; (17)
; (18)
. (19)
Задача 4. Задача об оптимальном раскрое листового материала [5].
На заготовительный участок поступило некоторое количество листового материала, из которых необходимо получить (вырезать) заготовки n типов, причем число заготовок j-типа должно оказаться не меньшим Nj. Кроить листовой материал можно m способами, при каждом из которых получаются zi1 заготовок 1-го типа, zi2 – заготовок 2-типа и т.д. Исходные данные сведены в табл. 4.
Таблица 4
Исходные данные к задаче
| Способы раскроя | Число заготовок j-го типа, получаемых при раскрое i-м методом | |||||
| 1 | 2 | … | j | … | n | |
| 1 | z11 | z12 | ... | z1j | … | z1n |
| 2 | z21 | z22 | … | z2j | … | z2n |
| … | … | … | … | … | … | … |
| i | zi1 | zi2 | … | zij | … | zin |
| … | … | … | … | … | … | … |
| m | zm1 | zm2 | … | zmj | … | zmn |
| Требуемое количество заготовок | N1 | N2 | … | Nj | … | Nn |
Если обозначить xi – число листов раскраиваемых i-м способом, то математически можно записать задачу минимизации ЦФ:
, (20)
при ограничениях:
(21)
(22)
Задача 5. Задача нахождения наиболее рационального способа использования сырья и материалов [3].
Предприятие может выпустить три вида продукции: П1, П2, П3. Для выпуска продукции требуются ресурсы трех видов: трудовые, станочное оборудование и полуфабрикаты. Определить, в каком количестве и какого вида продукции надо выпустить, чтобы прибыль от ее реализации была максимальной. Объемы и нормы расхода ресурсов приведены в условных обозначениях в табл. 5.
Таблица 5
Исходные данные к задаче
| Наименование ресурса | Вид продукции | Объем ресурса | ||
| П1 | П2 | П3 | ||
| Расход ресурса на единицу продукции | ||||
| Трудовые ресурсы, человеко-час | a1 | а2 | а3 | а |
| Станочное оборудование, станко-смена | b1 | b2 | b3 | b |
| Полуфабрикаты, кг | с1 | с2 | с3 | с |
| Прибыль с единицы продукции, руб. | p1 | p2 | p3 | max |
| Выпуск, шт. | xl | х2 | х3 | |
2.4. Методика применения Microsoft EXCEL для решения ЗЛП [6]
Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
1) Ввести условие задачи:
1. создать экранную форму для ввода условия задачи: переменных, целевой функции (ЦФ), ограничений, граничных условий;
2. ввести исходные данные в экранную форму: коэффициенты ЦФ, коэффициенты при переменных в ограничениях, правые части ограничений;
3. ввести зависимости из математической модели в экранную форму: формулу для расчета ЦФ, формулы для расчета значений левых частей ограничений;
4. задать ЦФ (в окне "Поиск решения"): целевую ячейку, направление оптимизации ЦФ;
5. ввести ограничения и граничные условия (в окне "Поиск решения"): ячейки со значениями переменных, граничные условия для допустимых значений переменных, соотношения между правыми и левыми частями ограничений.
2) Решить задачу:
1. установить параметры решения задачи (в окне "Поиск решения");
2. запустить задачу на решение (в окне "Поиск решения");
3. выбрать формат вывода решения (в окне "Результаты поиска решения").
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
(23)
Ввод исходных данных
1. Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (23) вместе с введенными в нее исходными данными представлена на рис.1.
Рис.1. Экранная форма задачи (23) (курсор в ячейке F6)
В экранной форме на рис.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи (23) соответствуют ячейки B3 (x1), C3 (x2), D3 (x3), E3 (x4), коэффициентам ЦФ соответствуют ячейки B6 (c1=130,5), C6 (c2=20), D6 (c3=56), E6 (c4=87,8), правым частям ограничений соответствуют ячейки H10 (b1=756), H11 (b2=450), H12 (b3=89) и т.д.
2. Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (23) значение ЦФ определяется выражением 
(24)
Используя обозначения соответствующих ячеек в Excel (см. рис.1), формулу для расчета ЦФ (24) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6), то есть B6·B3+C6·C3+D6·D3+E6·E3 (25)
Чтобы задать формулу (25) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу "Enter" =СУММПРОИЗВ(B$3:E$3;B6:E6) (26)
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись B6:E6 указывает на ячейки B6, C6, D6 и E6). После этого в целевой ячейке появится 0 (нулевое значение) (рис.2).
Рис.2. Экранная форма задачи (23) после ввода всех необходимых формул
(курсор в ячейке F6)
Примечание 1. Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки “ fx ” на стандартной панели инструментов. Так, например, формулу (26) можно задать следующим образом: курсор в поле F6; нажав кнопку “ fx ”, вызовите окно "Мастер функций – шаг 1 из 2"; выберите в окне "Категория" категорию "Математические"; в окне "Функция" выберите функцию СУММПРОИЗВ; в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$3:E$3, а в строку "Массив 2" – выражение B6:E6 (рис.3);
после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Рис.3. Ввод формулы для расчета ЦФ в окно "Мастер функций"
3. Ввод зависимостей для левых частей ограничений
Левые части ограничений задачи (23) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 – 1-е ограничение; B11, C11, D11, E11 – 2-е ограничение и B12, C12, D12, E12 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.6.
Как видно из табл.6, формулы, задающие левые части ограничений задачи (23), отличаются друг от друга и от формулы (26) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (с помощью правой кнопки «мыши» и выпадающего окна и команды «Копировать» или клавишами "Ctrl-Insert");
Таблица 6
Формулы, описывающие ограничения модели (23)
| Левая часть ограничения | Формула Excel |
 или
| =СУММПРОИЗВ(B$3:E$3;B10:E10) |
 или
| =СУММПРОИЗВ(B$3:E$3;B11:E11) |
 или
| =СУММПРОИЗВ(B$3:E$3;B12:E12) |
помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (с помощью правой кнопки «мыши» и выпадающего окна и команды «Вставить» или клавишами "Shift-Insert") (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис.2).
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис.4 и 5).
Рис. 4. Проверка правильности введения формулы в целевую ячейку F6
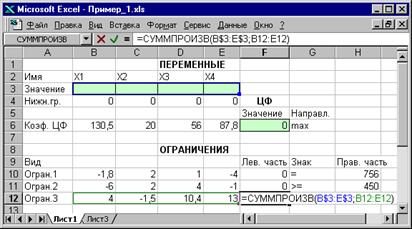
Рис. 5. Проверка правильности введения формулы в ячейку F12
для левой части ограничения 3
4. Задание ЦФ
Дальнейшие действия производятся в окне "Поиск решения", которое вызывается из меню "Сервис" (рис.6): поставьте курсор в поле "Установить целевую ячейку";
введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме ¾ это будет равносильно вводу адреса с клавиатуры;
введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке "максимальному значению".
Рис. 6. Окно "Поиск решения" задачи (23)
5. Ввод ограничений и граничных условий
Задание ячеек переменных
В окно "Поиск решения" в поле "Изменяя ячейки" впишите адреса $B$3:$E$3. Необходимые адреса можно вносить в поле "Изменяя ячейки" и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис.1).
Нажмите кнопку "Добавить", после чего появится окно "Добавление ограничения" (рис.7). В поле "Ссылка на ячейку" введите адреса ячеек переменных $B$3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме. В поле знака откройте список предлагаемых знаков и выберите 
. В поле "Ограничение" введите адреса ячеек нижней границы значений переменных, то есть $B$4:$E$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
Рис. 7. Добавление условия неотрицательности переменных задачи (23)
Задание знаков ограничений 
, , =
Нажмите кнопку "Добавить" в окне "Добавление ограничения". В поле "Ссылка на ячейку" введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме. В соответствии с условием задачи (23) выбрать в поле знака необходимый знак, например =. В поле "Ограничение" введите адрес ячейки правой части рассматриваемого ограничения, например $H$10. Аналогично введите ограничения: $F$11>=$H$11, $F$12<=$H$12. Подтвердите ввод всех перечисленных выше условий нажатием кнопки OK.
Окно "Поиск решения" после ввода всех необходимых данных задачи (23) представлено на рис. 6. Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки "Изменить" или "Удалить" (см. рис. 6).
Решение задачи
1. Установка параметров решения задачи
Задача запускается на решение в окне "Поиск решения". Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку "Параметры" и заполнить некоторые поля окна "Параметры поиска решения" (рис.8).
Рис.8. Параметры поиска решения, подходящие для большинства задач ЛП
Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32767 секунд (более 9 часов).
Параметр "Предельное число итераций" служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32767.
Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр "Сходимость" применяется только при решении нелинейных задач.
Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки "OK".
2. Запуск задачи на решение
Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить".
После запуска на решение задачи ЛП на экране появляется окно "Результаты поиска решения" с одним из сообщений, представленных на рис.9, 10 и 11.
Иногда сообщения, представленные на рис.10 и 11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует. Если при заполнении полей окна "Поиск решения" были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено.
Рис.9. Сообщение об успешном решении задачи
Рис.10. Сообщение при несовместной системе ограничений задачи
Рис.11. Сообщение при неограниченности ЦФ в требуемом направлении
Иногда слишком малое значение параметра "Относительная погрешность" не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне "Результаты поиска решения" представлены названия трех типов отчетов: "Результаты", "Устойчивость", "Пределы". Они необходимы при анализе полученного решения на чувствительность.
Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку "OK". После этого в экранной форме появляется оптимальное решение задачи (рис.12).
Анализ оптимального решения
Анализ оптимального решения начинается после успешного решения задачи, когда на экране появляется диалоговое окно «Результат поиска решения». Решение найдено см. рис.9. С помощью этого диалогового окна можно вызвать отчеты трех типов: "Результаты", "Устойчивость", "Пределы". Отчеты каждого типа могут быть вызваны по следующему алгоритму.
Алгоритм 1. Вызов отчетов анализа. На экране: диалоговое окно «Результат поиска решения» Решение найдено (рис. 9).
1. Курсор на тип вызываемого отчета. Начнем с Отчета по результатам, т.е. "Результаты".
2. ОК. На экране появится вызванный отчет на новом листе, на ярлычке которого указано название отчета.
3. Курсор на ярлычок с названием отчета.
4. Щелчок левой кнопкой мыши один раз. На экране: вызванный отчет.
Рис.12. Экранная форма задачи (23) после получения решения
Отчет по результатам
Отчет состоит из трех таблиц:
Таблица 1 приводит сведения о ЦФ. В столбце Исходно приведены значения целевой функции до начала вычислений.
Таблица 2 приводит значения искомых переменных, полученные в результате решения задачи.
Таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Для Ограничений в графе Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения; в графе Значение приведены величины использованного ресурса: в графе Разница показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние указывается связанное; при неполном использовании ресурса в этой графе указывается не связан.
Для Граничных условий приводятся аналогичные величины с той лишь разницей, что вместо величины неиспользованного ресурса показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Отчет по устойчивости
Отчет по устойчивости состоит из двух таблиц.
В таблице 1 приводятся следующие значения для переменных:
результат решения задачи;
редуцированная стоимость, т.е. дополнительные двойственные переменные, которые, показывают, насколько изменяется целевая функция при принудительном включении единицы переменной (например, продукции типа 1) в оптимальное решение;
коэффициенты целевой функции;
предельные значения приращения коэффициентов целевой функции, при которых сохраняется набор переменных, входящих в оптимальное решение.
В таблице 2 приводятся аналогичные значения для ограничений:
величина использованных ресурсов;
теневая цена, т.е. двойственные оценки, которые показывают как изменится ЦФ при изменении ресурсов на единицу;
значения приращения ресурсов, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.
Отчет по пределам
В нем показано, в каких пределах может изменяться переменные (например, выпуск продукции), вошедшей в оптимальное решение, при сохранении структуры оптимального решения: приводятся значения переменных в оптимальном решении; приводятся нижние пределы изменении значений переменных. Например, в отчете могут быть указаны значения целевой функции при выпуске данного типа продукции на нижнем пределе.
Далее приводятся верхние пределы изменения переменных и значения ЦФ при выпуске продукции, вошедшей в оптимальное решение на верхних пределах.
2.5. Методика применения программы «Решение и моделирование задач линейного программирования» [4]
Программа написана на алгоритмическом языке Visual Basic for Application (VBA) и оформлена в виде модуля табличного процессора Excel и позволяет решать ЗЛП для детерминированных исходных данных, а также проводить имитационное моделирование для линейных моделей при стохастических исходных данных для оценивания параметров распределения вероятностей переменных оптимального плана и значения целевой функции.
Решение детерминированной задачи. Для решения ЗЛП с помощью программы необходимо привести систему ограничений к стандартной форме с выделенной единичной матрицей коэффициентов системы ограничений. Все переменные модели разделятся на исходные, дополнительные и искусственные. Например, рассмотрим исходную линейную модель следующего вида:
min z = 4x1 + x2
3x1 + x2 = 3;
4x1 + 3x2 і 6;
x1 + 2x2 Ј 4;
xi і 0.
Приводим модель к стандартной форме, вводя дополнительные переменные:
min z = 4x1 + x2
3x1 + x2 = 3;
4x1 + 3x2 - x3 = 6;
x1 + 2x2 + x4 = 4;
xi і 0.
Матрица коэффициентов системы ограничений имеет вид:
.
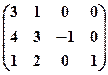Для выделения единичной матрицы коэффициентов (и допустимого базисного решения) в матрицу вводятся дополнительные искусственные единичные вектор-столбцы таким образом, чтобы единичная матрица занимала последние m столбцов. Целесообразно провести введение дополнительных вектор-столбцов так, чтобы единичная матрица имела диагональный вид:
.
В данной матрице 4-й и 5-й столбцы являются искусственными. Система ограничений, соответствующая этой матрице, имеет вид:
3x1 + x2 + x4 = 3
4x1 + 3x2 - x3 + x5 = 6
x1 + 2x2 + x6 = 4
xi і 0
Искусственные переменные вводятся в целевую функцию со штрафом М:
min z = 4 x 1 + x 2 + Mx 4 + Mx 5, где М – коэффициент, заведомо больший любого числа, с которым он будет сравниваться.
Таким образом, модель содержит 6 переменных, из них x1 и х2 - исходные, х3 и х6 - дополнительные, х4 и х5 - искусственные. Искусственные переменные вводятся в целевую функцию со штрафом М (в задаче максимизации искусственные переменные входят в целевую функцию со штрафом -М). Исходные данные модели имеют вид:
= (4; 1; 0; М; М; 0) - вектор коэффициентов целевой функции;
А = - матрица коэффициентов системы ограничений;
- вектор правых частей системы ограничений.
Вектор целевой функции раскладывается на два слагаемых:
,
где 
содержит коэффициенты при исходных переменных, а 
- при искусственных. Для рассматриваемой модели: = (4; 1; 0; 0; 0; 0), 
= (0; 0; 0; 1; 1; 0).
Примечание. Если решается задача максимизации, то ненулевые компоненты вектора равны -1.
Для запуска программы надо загрузить в табличный процессор EXCEL файл zlp1.xls и активировать лист Расчет, на котором находятся 4 управляющие кнопки и, возможно, результаты предыдущего расчета. Для начала работы с программой необходимо заполнить исходную таблицу на листе Расчет. В исходную таблицу вводятся следующие значения:
1) число переменных задачи n, то есть размерность вектора 
;
2) число ограничений m, то есть количество строк в матрице А;
3) признак оптимизации, равный 1, если решается задача максимизации и 0, если решается задача минимизации;
4) число этапов моделирования (при решении ЗЛП с детерминированными исходными данными число этапов принимается равным 1).
В рассматриваемом случае исходная таблица имеет вид:
Таблица 6.
| 1 | Число переменных | 6 |
| 2 | Число ограничений | 3 |
| 3 | Признак оптимизации | 0 |
| 4 | Число этапов моделирования | 1 |
После заполнения исходной таблицы нужно нажать кнопку "Формирование таблиц". На лист Расчет будут выведены следующие таблицы для ввода детерминированных исходных данных ЗЛП:
1) "Коэффициенты целевой функции" - массив для ввода коэффициентов сj целевой функции при исходных переменных задачи (вектор );
2) "Фиктивные слагаемые коэффициентов целевой функции" - массив для ввода признаков искусственных переменных (вектор );
3) "Номера базисных переменных" - массив с номерами переменных xj , которые используются в качестве переменных начального базиса. Если в задаче были введены искусственные переменные, то целесообразно их использование для формирования начального базиса.
4) "Матрица коэффициентов" - таблица для ввода матрицы удельных расходов ресурсов А и вектора запасов ресурсов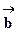 
.
После ввода исходных данных ЗЛП в таблицы листа Расчет запуск модуля, реализующего вычисления симплекс-метода, производится нажатием кнопки "Решение ЗЛП", при этом исходные данные модели должны соответствовать ЗЛП в стандартной форме.
Наиболее эффективно использование модуля программы, использующего симплекс-метод, для моделей с выделенным начальным допустимым базисным решением. В качестве переменных начального базиса обычно выбирают искусственные переменные, а если они в исследуемой модели не используются, то в качестве переменных начального базиса выбирают дополнительные переменные. Для анализа полученного результата с помощью соотношений двойственности целесообразно (но необязательно) переменным начального базиса отводить последние m мест в векторе переменных . Тогда матрица А удельных расходов ресурсов будет в последних m столбцах содержать единичную матрицу. Номера базисных переменных вводятся в соответствующую таблицу на листе Расчет.
Для правильной отработки программы при нажатии клавиши "Решение ЗЛП" необходимо, чтобы выполнялись следующие ограничения: 2 Ј n Ј 50 , 2 Ј m Ј 50, признак оптимизации равен 1 (соответствует задаче максимизации) или 0 (соответствует задаче минимизации).
Следует помнить, что после заполнения таблицы исходных данных ЗЛП нельзя менять значения n (число переменных) и m (число ограничений) в исходной таблице на листе Расчет перед нажатием кнопки "Решение ЗЛП".
После отработки модуля программы, реализующего алгоритм симплекс-метода, на лист Расчет выводится результирующая симплекс-таблица с одним из следующих сообщений:
1) "Условие оптимальности выполняется";
2) "Неограниченная ОДР".
В первом случае результирующая симплекс-таблица соответствует оптимальному решению ЗЛП с искусственными переменными, которое совпадает с оптимальным решением исходной задачи, если все искусственные переменные равны 0. Искусственные переменные равны 0, если они не входят в состав базисных переменных или их значения равны 0 в столбце "правые части" результирующей таблицы. Если искусственные переменные отсутствуют в оптимальном базисе, то данные таблицы могут быть использованы для дальнейшего анализа. Если искусственные переменные присутствуют в оптимальном базисе, то исходная задача не имеет допустимых решений. Во втором случае результирующая симплекс-таблица соответствует итерации симплекс-метода, на которой была обнаружена невозможность получения оптимального решения из-за неограниченности ОДР.
Для рассматриваемого примера после нажатия кнопки "Формирование таблиц" на лист Расчет выводятся таблицы, в которые заносятся исходные данные модели в следующем виде.
Таблица 7
Коэффициенты целевой функции
| N | 1 | 2 | 3 | 4 | 5 | 6 |
| c | 4 | 1 | 0 | 0 | 0 | 0 |
Таблица 8
Дата добавления: 2021-02-10; просмотров: 339; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!