Действия над событиями. Соотношения между событиями

⇐ ПредыдущаяСтр 2 из 2

Суммой, или объединением, двух событий называется событие, состоящее в появлении хотя бы одного из них. Сумма событи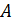й и 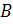обозначается как .

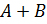Аналогично определяется и обозначается сумма 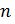событий – т.е. событие, состоящее в появлении хотя бы одного из них. Сумму 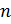событий 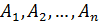обозначают так: А₁+А₂+…+А_n= .

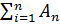Произведением или пересечением двух событий называется событие, состоящее в одновременном их появлении. Произведение событий 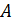и 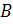обозначается через 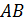. Аналогично определяется произведение n событий. Произведение n событий 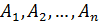обозначают: .

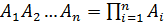Сложение и умножение вероятностей

Теорема сложения вероятностей формулируется следующим образом:

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т.е. .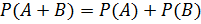

Обобщим теорему на случай трех событий. Обозначая событие 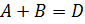и присоединяя к сумме еще одно событие С, легко доказать, что

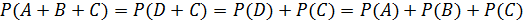Методом полной индукции можно обобщить теорему сложения на произвольное число несовместных событий. Таким образом, теорему сложения вероятностей удобно записать в виде: .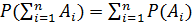

Следствие 1. Если события А₁, А₂, ... А_n образуют полную группу несовместных событий, то сумма их вероятностей равна 1, т.е. .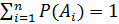

Следствие 2. Сумма вероятностей противоположных событий равна 1:

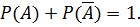
Следствие 3. В случае, когда события 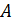и 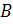совместны, то вероятность суммы этих событий выражается формулой: .

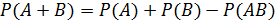Аналогичным образом вероятность суммы трех совместных событий вычисляем по формуле .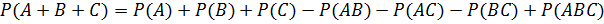

Методом полной индукции можно доказать общую формулу для вероятности суммы любого числа совместных событий:

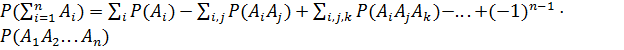Теорема умножения вероятностей

Перед тем, как излагать теорему умножения вероятностей, введем еще одно важное понятие: понятие о независимых и зависимых событиях.

Событие 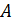называется независимым от события В, если вероятность события 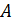не зависит от того, произошло событие 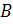или нет. Событие 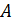называется зависимым от события В, если вероятность события 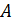меняется в зависимости от того, произошло событие 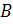или нет.

Рассмотрим примеры:

1) Опыт состоит в бросании 2x монет. Событие 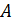– выпал герб на 1-ой монете; 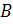– выпал герб на второй монете. В данном случае вероятность события 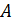не зависит от того, произошло событие 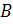или нет. Событие 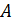независимо от события .

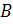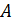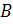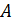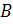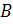2) В урне 2 белых шара и один черный. Два человека вынимают из урны по одному шару. Событие - белый шар у первого человека; - белый шар у второго человека. Вероятность до того, как известно что-либо о , равна . Если известно, что - произошло, то вероятность 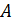становится равной , из чего следует, что событие 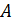зависит от события .

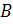Вероятность события 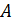, вычисленная при условии, что имело место другое событие 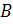, называется условной вероятностью события А, и обозначается .

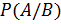Для условий последнего примера 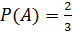; 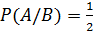. Условия независимости события 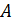от события 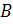можно записать как 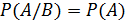, условия зависимости - .

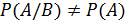Теорема умножения вероятностей формулируется следующим образом:

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место

(*)

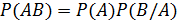Следствие 1. Если событие 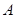не зависит от события 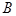, то и событие 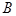не зависит от события .

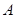Дадим другое определение независимости событий. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого. Понятие независимости событий может быть распространено на случай произвольного числа событий. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.

Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий. Это следствие непосредственно вытекает из определения независимых событий.

Теорема умножения вероятностей может быть обобщена на случай произвольного числа событий. В общем виде она формулируется следующим образом: вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место

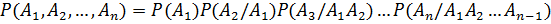
Доказательство проводится методом полной индукции. В случае независимых событий теорема упрощается и принимает вид: 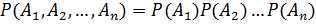, т. е. вероятность произведения независимых событий равна произведению вероятностей этих событий или .

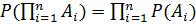Пример 1. В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Какова вероятность того, что оба шара белые?

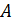- появление двух белых шаров, 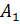- белый шар при первом вынимании, 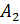- белый шар при втором вынимании; 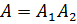. По теореме .

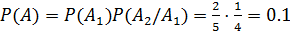Пример 2. Те же условия, но после первого вынимания шар возвращается в урну, затем шары перемешиваются. Тогда .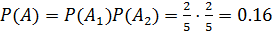

Формула полной вероятности

Следствием обеих теорем - теоремы сложения и умножения - является так называемая формула полной вероятности. Пусть требуется определить вероятность некоторого события 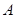, которое может произойти вместе с одним из событий 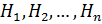, образующих полную группу несовместных событий. Будем называть эти события гипотезами. Докажем, что в этом случае 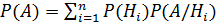, т. е. вероятность события 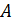вычисляется как сумма произведений вероятности любой гипотезы на вероятность события при этой гипотезе. Эта формула носит название формулы полной вероятности.

Пример. На фабрике, изготовляющей болты, первая машина производит 30%, вторая- 25%, третья- 45% всех изделий. Брак в их продукции составляет соответственно 2%, 1% и 3%. Найти вероятность того, что случайно выбранный болт оказался дефектным.

Решение. Обозначим через 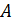событие, состоящее в том, что случайно выбранный болт – дефектный, а через 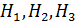– события, состоящие в том, что этот болт произведен соответственно 1-ой, 2-ой и 3-ей машинами. Из условия задачи следует, что 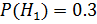, , 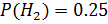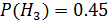; 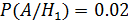, , 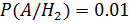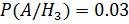. По формуле полной вероятности получаем, что 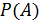=0.3·0.02+0.25·0.01+0.45·0.3=0.022.

Теорема гипотез. (Формула Байеса)

Следствием теоремы умножения и формулы полной вероятности является так называемая гипотез, или формула Байеса. Поставим следующую задачу. Имеется полная группа несовместных гипотез 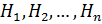. Вероятности этих гипотез до опыта известны и равны соответственно 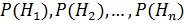. Произведен опыт, в результате которого наблюдено появление некоторого события 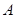. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события? Здесь, по существу, речь идет о том, чтобы найти условную вероятность 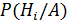для каждой гипотезы. По теореме умножения имеем 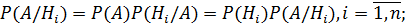или, отбрасывая левую часть, 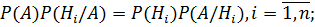откуда 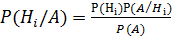, при 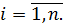Выражая Р(А) с помощью формулы полной вероятности, имеем

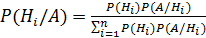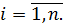
Пример. Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго - 0,4. После стрельбы по мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку.

Решение. До опыта возможны следующие гипотезы: 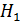- ни первый, ни второй не попадут; 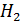- оба попадут; 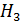- первый попадет, второй - нет; 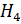- первый не попадет, второй попадет. Вероятности этих гипотез следующие: 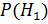=0,2×0,6=0,12; 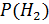=0,32; 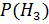=0,8×0,6=0,48; 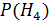=0,2×0,4=0,08. Условные вероятности наблюденного события 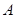при этих гипотезах: 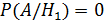; ; 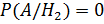; 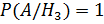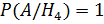. Тогда .

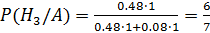Задачи

1. Сколькими способами можно выбрать 5 радиоламп из15?

2. Из 20 человек рабочих составляют бригаду в 5 человек. Сколько по составу бригад может быть образовано?

3. Из 20 хорошо обученных пилотов составляется экипаж. Экипаж состоит из штурмана, радиста и стрелка. Сколькими способами может быть укомплектован экипаж?

4. Сколько различных диагоналей можно провести в восьмиугольнике?

5. Сколькими способами группа из 5 человек может быть размещена в ряд?

6. Сколькими способами можно распределить 1, 2, 3 премию на конкурсе, в котором принимали участие 20 человек?

7. Сколько словарей нужно издать, чтобы можно было выполнять переводы с каждого из 5 языков на любой из этих языков?

8. В турнире принимают участие 8 шахматистов. Два шахматиста встречаются 1 раз. Сколько партий было сыграно в турнире?

9. Бросают две игральные кости. Сколько вариантов исхода этого опыта может быть?

10. Рассыльному поручено разнести телеграммы по 5 адресам. Сколько различных маршрутов он может выбрать?

11. При встрече 9 человек обменялись рукопожатиями. Сколько сделано рукопожатий?

12. Девять человек обменялись фотографиями. Сколько было заказано фотографий?

13. Бросаются одновременно две игральные кости. Какова вероятность того, что сумма выпавших очков равна 6?

14. Участники жеребьевки тянут жетоны с номерами от 1 до 100. Какова вероятность того, что номер первого наудачу извлеченного жетона не содержит цифру 5?

15. Владелец карточки 5 из 36 зачеркивает 5 номеров. Какова вероятность того, что им будут угаданы все 5 номеров в очередном тираже?

16. В магазин поступило 30 новых цветных телевизоров, среди которых 5 имеют скрытые дефекты. На удачу отбирается 1 телевизор для проверки. Какова вероятность, что он не имеет скрытых дефектов?

17. 3. В ящике 15 деталей, среди которых 10 окрашенных. Сборщик на удачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными? С какой вероятностью среди извлеченных деталей окажутся 2 окрашенные и 1 неокрашенная детали?

18. В ящике находится 15 красных, 9 голубых и 6 зеленых шаров. На удачу достали 6 шаров. Какова вероятность того, что среди них 1– зеленый, 2– голубых, 3– красных?

19. На удачу выбрано натуральное число не превосходящее 10. Какова вероятность того, что это число является простым?

20. Множество Е состоит из 10 первых букв русского алфавита. Опыт состоит в выборе без возвращения и записи слова в порядке поступления букв. а) сколько четырехбуквенных слов может быть получено в данном опыте? б) какова вероятность того, что составленное слово будет оканчиваться буквой а.

21. Определить вероятность того, что выбранное на удачу целое число будет оканчиваться на цифру 1.

22. В урне 11 белых и 6 черных шаров. Выбираются все шары. С какой вероятностью последний будет черный?

23. На пяти одинаковых карточках написаны буквы и, к, м, н, с. Карточки перемешиваются и раскладываются в ряд. С какой вероятностью получится слово Минск?

24. После бури на участке между 40 и 70 километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 50-ым и 55-ым километрами линии?

25. Три стрелка стреляют в цель независимо друг от друга. Первый стрелок попадает в цель с вероятностью 0,6, второй – с вероятностью 0,7, а третий – с вероятностью 0,75. Какова вероятность хотя бы одного попадания в цель, если каждый стрелок сделает по одному выстрелу.

26. Вероятность того, что будет дождь – 0,35, снег – 0,7. Какова вероятность плохой погоды, если вероятность дождя со снегом равна 0,15.

27. Достаточным условием сдачи коллоквиума является ответ на один из двух вопросов, заданных преподавателем. Студент не знает 8 ответов из тех 40, которые могут быть заданы. Какова вероятность сдачи коллоквиума этим студентом?

28. В коробке 3 красных и 7 синих шариков. Наудачу извлекается один шарик, а затем второй. Найти вероятность того, что первый шарик красный, а второй синий.

29. Два студента независимо друг от друга ищут в библиотеках города одну книгу. Вероятность того, что книгу найдет первый студент – 0,7, второй – 0,9. Какова вероятность того, что книгу найдет только один студент.

30. Три стрелка произвели по одному выстрелу по цели. Вероятность попадания для первого стрелка – 0,7, для второго – 0,8, для третьего – 0,9. Найти вероятность: а) трех попаданий; б) только двух попаданий; в) хотя бы одного попадания.

31. В группе десять студентов решают задачу. Из них два студента учатся на «5», пять – на «4», три – на «3». Вероятность того, что задача будет решена отличником – 0,9, хорошистом – 0,8, троечником – 0,5. Какова вероятность решения задачи одним из студентов?

32. При разрыве снаряда образуется 10% крупных осколков, 60% – средних, 30% – мелких. Вероятность пробивания брони крупным осколком – 0,7, средним – 0,2, мелким – 0,05. Известно, что в броню попал осколок. С какой вероятностью броня пробита?

33. Из десяти винтовок четыре снабжены оптическим прицелом. Вероятность попадания в мишень из винтовки с оптическим прицелом равна 0,95, из винтовки без оптического прицела – 0,8. Стрелок поразил мишень из наудачу выбранной винтовки. Найти вероятность того, что стрелок стрелял из винтовки без прицела.

34. В канцелярии работает 4 секретарши, которые отправляют 40, 10, 30, и 20 процентов исходящих бумаг соответственно. Вероятность неверной адресации бумаг секретаршами равны соответственно 0.01, 0.04, 0.06, 0.01. Найти вероятность того, что неверно адресованный документ отправлен третьей секретаршей.

Дата добавления: 2021-02-10; просмотров: 108; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!