Теорема сложения для любых двух событий
Теорема. Для любых двух событий А и В вероятность наступления суммы равна:
Р(А+В)=Р(А)+Р(В)-Р(АВ).
Доказательство
Пусть n – общее число исходов, m1 – число исходов, благоприятных событию А, m2 – число исходов, благоприятных событию В, k - число исходов, благоприятных событию А и событию В одновременно.
А+В благоприятствует m1+m2-k, Р(А+В)=( m1+m2-k)/n= (m1/n)+(m2/n)-(k/n).
Определение
Два события A и B называются независимыми, если вероятность появления одного из них не зависит от вероятности появления другого.
Пример. В корзине два белых и два черных шара. Событие A – « вынимают один белый шар». P(A)=1/2.
а) Шар кладут обратно и вынимают 1 шар.
B – «вынимают черный шар». P(B)=1/2
б) вынимают еще один шар (без возвращения)
P(B)=2/3
В случае а) вероятность события B не зависит от вероятности появления события A. В случае б) вероятность наступления события B зависит от события A, то есть события A и B зависимы.
Теорема
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий P(AB)=P(A)P(B)
Следствие.
Если A1,…,An – независимые события, то P(A1. ….An)=P(A1). ….P(An).
Условная вероятность
Если никаких ограничений при вычислении вероятностей на событие не накладывается, то такая вероятность называется безусловной. Если же налагаются и другие условия, то вероятность событий называется условной.
Определение.
Условной вероятностью называется вероятность события B, вычисленное предложение, что событие A уже наступило. PA(B) или P(A/B).
|
|
|
Теорема
Вероятность произведения двух зависимых событий равна произведению вероятности первого события на условную вероятность второго события.
Р(А.В)=Р(А).РА(В) (1)
Доказательство следует из определения условной вероятности.
Замечание. Если формулу (1) применить к событию В.А, то
Р(В.А)==Р(В).Р(А). Так как Р(А.В)=Р(В.А), то Р(А).РА(В)=Р(В).РВ(А).
Если события А и В – независимы, то условия вероятности события В равно его безусловной вероятности. Р(В)=РА(В) и Р(А)=РВ(А).
Теорема
Вероятность произведения n – независимых событий можно вычислить по формуле:
Р( А1.А2.….Аn)=Р(А1).РА1(А2).РА1А2(А3).….РА1…Аn(Аn)
Теорема
Вероятность наступления хотя бы одного из n-событий равна:
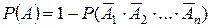
А – наступление хотя бы одного из n событий.
а) для зависимых событий: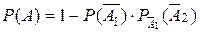 
.
б) для независимых событий: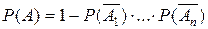 
.
в) если вероятность всех событий равна одному и тому же числу, то 
, где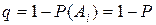 
.
Формулы полной вероятности и Байеса
Пусть Н1, Н2, …, Нn – некоторые попарно несовместные события и пусть А может произойти вместе с одним из этих событий. Тогда А(Н1+Н2+…+Нn)= АН1+АН2+ …+АНn, т.е. мы представили событие А в виде суммы попарно несовместных событий. Применяя теоремы сложения и умножения, получим
|
|
|
Р(А)=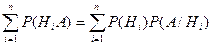 
(1)
Формула (1) называется формулой полной вероятности. В реальном опыте Нi образуют полную группу несовместных событий и называются гипотезами.
Пример 1. В первой урне 10 шаров, из них 4 белых; во второй урне 8 шаров, из них 5 белых. Из первой урны наудачу извлекли один шар и переложили его во вторую. Затем из второй урны наудачу извлекли один шар. Какова вероятность, что извлеченный из второй урны шар белый?
Решение. Пусть событие А означает, что из второй урны извлечен белый шар. Введем гипотезы: Н1-переложили белый шар, Н2-переложили небелый шар. События Н1 и Н2 несовместны, образуют полную группу событий, а событие А может осуществиться только с одной из них, т.е. АÌН1+Н2. Воспользуемся формулой (1). Поскольку все исходы опыта извлечения шара из урны, равновозможные (на это указывает слово «наудачу»), то воспользуемся классическим определением вероятности. Всего случаев n=10, благоприятных гипотезе Н1 четыре, а гипотезе Н2 – шесть. Поэтому Р(Н1)= 
, Р(Н2)= =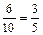 
.
Если произошло событие Н1, то во второй урне из 9 шаров будет 6 белых, следовательно Р(А/Н1)=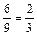 
. Если произошло событие Н2, то во второй урне из 9 шаров останется 5 белых, следовательно, Р(А/Н2)= 
. Подставляя все найденные значения в (1), получим Р(А)=Р(Н1)Р(А/Н1)+ Р(Н2)Р(А/Н2)=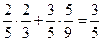 
.
|
|
|
Воспользуемся определением условной вероятности
Р(Нk/А)=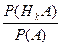 
(2)
Используя теорему умножения и формулу полной вероятности, из (2) получим
Р(Нk/А)=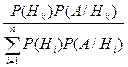 
(3)
Равенство (3) носит название формулы Байеса. Она определяет вероятность гипотезы после того, как произошло событие А.
Пример 2. В первой урне 10 шаров, из них 4 белых; во второй урне 8 шаров из них 5 белых. Из первой урны наудачу извлекли один шар и переложили его во вторую. Затем из второй урны наудачу извлекли один шар. Он оказался белым. Что вероятнее, из первой урны во вторую был переложен белый или небелый шар?
Решение. Введем те же гипотезы Н1, Н2 и то же событие А, что и в задаче примера 1. Чтобы решить задачу, нам нужно найти условные вероятности P(H1/A) и P(H2/A) и сравнить их. Воспользуемся формулой Байеса (3) и результатами примера 1. Получим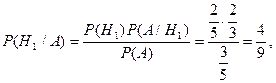 
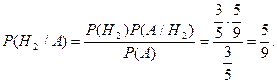
Т.к. P(H2/A)>P(H1/A), то вероятнее, что из первой урны во вторую был переложен небелый шар.
Дата добавления: 2021-01-21; просмотров: 69; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!