Классический подход к сложению и умножению вероятностей
Лекция №4
Вопросы:
Операции над событиями.
Классический подход к сложению и умножению вероятностей.
Формула полной вероятности. Формула Байеса.
Операции над событиями
Поскольку случайные события отождествляются с множеством, а над множеством можно производить операции сложения, умножения и др., то и над случайными событиями, очевидно, можно производить аналогичные операции.
Если всякое элементарное событие ω из А входит также и в В, то пишут АÌВ. Говорят, А есть подмножество множества В, событие А влечет за собой событие В, событие А – частный случай события В. Если АÌВ и ВÌА, то события А и В называют равными. Пишут А=В.
Суммой (объединением) событий А и В называют событие С, состоящее из всех элементарных событий, принадлежащих по крайней мере одному из событий А или В. Пишут С=А+В или С=АÈВ. В реальном опыте сумма А+В означает, что произошло либо событие А, либо событие В, либо оба вместе.
Понятие суммы можно распространить на n событий:
Произведением (пересечением) событий А и В называют событие С, состоящее из элементарных событий, принадлежащих и событию А, и событию В. Пишут С=АВ или С=АÇВ. В реальном опыте произведение АВ означает, что произошло и событие А, и событие В.
Понятие произведения можно распространить на n событий:
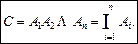
Разностью двух событий А и В называют событие С, состоящее из элементарных событий, принадлежащих событию А, но не принадлежащих событию В. Пишут С=А-В, или С=А\В. В реальном опыте разность А-В означает, что происходит событие А, а событие В не происходит.
|
|
|
Событие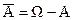 
называют противоположным событию А или дополнением к А. Если АВ=Æ, то события А и В называют несовместными, в противном случае – совместными.
Пример 5. Опыт состоит из трех выстрелов по мишени. Пусть события А1, А2, А3 означают попадание в мишень при 1-ом, 2-ом, 3-ем выстрелах соответственно. Тогда
1) С1= А1+А2+А3 означает хотя бы одно попадание;
2) С2= А1А2А3 – попаданий ровно 3;
3) С3= А1-А2 – попадание при первом выстреле и не попадание при втором, что можно записать иначе С3= А1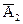 
;
4) 
– ни одного попадания, что можно записать иначе – 
;
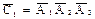5) 
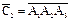– попаданий не 3, что можно записать иначе –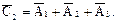 
 |
Отождествим случайное событие с множеством точек плоскости внутри замкнутой кривой. Тогда введенные операции над событиями легко проиллюстрировать геометрически с помощью так называемых диаграмм Венна.
На рис. 1- 4 заштрихованные части означают:
1) АВ; 2) А+В=А+В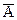 
; 3) А-В=А 
; 4)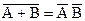 
.
Введенные операции над событиями удовлетворяют следующим свойствам:
1) А+В=В+А, АВ=ВА;
2) (А+В)+С=А+(В+С), (АВ)С=А(ВС);
3) (А+В)С=АС+ВС;
|
|
|
4) А+А=А, АА=А;
5) А+W=W, АW=А, А+Æ=А, АÆ=Æ;
6) А+ 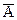= W, А 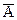= Æ;
7) А+В=А, АВ=В, если ВÌА;
8) если С=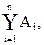 
то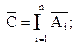 
9) если С=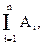 
то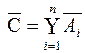 
.
Последние два свойства называют законами де-Моргана (отрицание суммы равно произведению отрицаний, отрицание произведения равно сумме отрицаний).
Классический подход к сложению и умножению вероятностей
Рассмотрим классический подход к теоремам сложения и умножения вероятностей событий.
Сложение вероятностей
Теорема (сложение вероятностей несовместных событий). Вероятность наступления суммы несовместных событий равна сумме вероятностей этих событий, т.е. Р(А+В)=Р(А)+Р(В).
Доказательство
Пусть n – общее число исходов, m1 – число исходов, благоприятных событию А, m2 - число исходов, благоприятных событию В. Тогда m1+m2 - число исходов, благоприятных наступлению события А или события В. Тогда по классическому определению вероятности имеем:
Р(А+В)= (m1+m2)/n= (m1/n)+(m2/n)=Р(А)+Р(В).
Следствие №1. Вероятность суммы n несовместных событий равна сумме вероятностей этих событий, т.е. Р(А1+…+Аn)=Р(А1)+…+Р(Аn)
Следствие №2. Если А1,…,Аn образуют полную группу. Но вероятность наступления хотя бы одного из них равна 1.
Следствие №3. Вероятность суммы события А и противоположного ему события равна 1, т.е. Р(А+ 
)=1.
|
|
|
Дата добавления: 2021-01-21; просмотров: 121; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!