Статическое определение вероятности
Классическое определение не всегда приемлемо, т.к. для его применения необходимо выполнение следующих условий:
Ø число элементарных исходов должно быть конечным
Ø все исходы должны быть равновозможными
На практике часто встречаются испытания, число исходов которых бесконечно, а так же часто невозможно представить результат испытаний в виде совокупности элементарных событий и трудно бывает указать основания, которые позволяют считать элементарные события равновозможными. Т.о. классическое определение является ограниченным, поэтому вводится определение статической вероятности.
Пусть произведено n испытаний в которых событие А произошло m раз.
Определение.
Число m называется абсолютной частотой события А, а число Р*(А)=m/n называется относительной частотой (или просто частотой) события А.
Пример: при транспортировке 10000 арбузов испортилось 26. Здесь
26 – абсолютная частота, Р*(А)=26/10000 – относительная частота, где А – испорченные арбузы.
Определение (статическое определение вероятности события).
Вероятность события А называется число, около которого группируются значения относительных частот при больших n, т.е. 
Р*(А)=Р(А).
Для статического определения вероятности характерно то. Что испытания производятся в действительности, а для классического определения это условие не обязательно.
Опыт по подбрасыванию монеты
| Опыт | Число опытов | m | m/n |
| Опыт Керриха | 10000 | 5087 | 0,5087 |
| Опыт Бюффона | 4040 | 2048 | 0,5069 |
| 1 опыт Пирсона | 12000 | 6019 | 0,5015 |
| 2 опыт Пирсона | 24000 | 12012 | 0,5005 |
Геометрическое определение вероятности
|
|
|
Геометрическое определение вероятности вводится для преодоления ограниченности классического определения, в частности для подсчета вероятности при бесконечном числе исходов.
Определение.
Геометрической вероятностью события А называется отношение меры области, благоприятствующей событию А, к мере всей области; т.е. Р(А)=meg(GA)/meg(G).
Пример: Найти вероятность того, что точка, случайно бросаемая в квадрат АВСD со стороной АВ=4 попадет в квадрат KLMN со стороной KL=3. Р(А)=SABCD/SKLMN=9/16.
Аксиоматическое определение вероятности
Пространство элементарных событий – это некоторое множество Ω, элементы которого ω называются элементарными событиями. При классическом определении вероятности Ω – множество всех равновозможных и попарно несовместных исходов опыта. В общем случае пространство элементарных событий не определяется, оно является понятием основным. Его можно только разъяснить на примерах.
Пример 1. Бросание игральной кости. При реальном бросании кости она может куда-нибудь закатиться, расколоться, стать на ребро или на вершину, если грунт мягкий, и т.д. В математической модели этого опыта мы отвлекаемся от многих несущественных моментов и считаем, что исходов опыта всего шесть: ω1, ω2,…, ω6. Множество этих взаимоисключающих исходов Ω={ωi}6i=1 – есть пространство элементарных событий.
|
|
|
Пример 2. Бросание двух игральных костей. Под элементарными событиями будем понимать размещения с повторениями из шести элементов по два: ω1ω1, ω1ω2, ω1ω3… Их число n = Ã62 = 36. Множество Ω={ωiωk}6i,k=1 – пространство элементарных событий.
Пример 3. Отказ прибора – событие случайное. Прибор может отказать в момент включения, а может проработать неопределенно долго. Поэтому под пространством элементарных событий будем понимать луч Ω={ω≥0}, а элементарным событием будем считать момент отказа, т.е. точку ω на этом луче. Элементарным событием можно считать и любой отрезок, левый конец которого совпадает с началом луча, ω={x:0£x£ω}. Очевидно, что число исходов этого опыта несчетное.
Пример 4. Стрельба по мишени. Введем в плоскости мишени декартову прямоугольную систему координат. Тогда каждому исходу опыта – попаданию в точку мишени, мы поставим в соответствие саму эту точку или упорядоченную пару чисел (x,y). Эта точка и будет элементарным событием. Вся мишень – пространство элементарных событий. Если мишень круглая радиуса r, а начало координат в центре, то Ω={(x,y): x2+y2 ≤ r2}. Очевидно, что число исходов опыта множество несчетное.
|
|
|
Уточним теперь понятие случайного события. Под случайным событием будем понимать всякое подмножество множества Ω. Само множество Ω назовем достоверным событием, а пустое множество Æ – невозможным событием. Подмножество А = {ω2, ω4, ω6} множества Ω пр.1. есть случайное событие, означающее выпадение четного числа очков. Подмножество В={ωiωi}i=16 множества Ω, пр.2. означает выпадение одинакового числа очков на обоих кубиках. Всякий интервал луча пр.3. и всякая область круга пр.4 отождествляются со случайным событием. Элементарные события, входящие в состав случайных событий, являются для них благоприятными
Пусть W - пространство элементарных событий, а 
– некоторая система подмножеств множества W, т.е. некоторое множество случайных событий.
Определение 1. Непустое множество называется алгеброй событий, если выполняются следующие аксиомы:
|
|
|
1) WÎ ;
2) если АÎ и ВÎ , то А+ВÎ , АВÎ и А-ВÎ .
Алгебра событий называется s - алгеброй, если вторая аксиома определения 1 распространена на бесконечную последовательность событий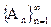 
, т.е. если АnÎ "nÎN, то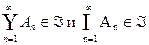 
.
Поскольку W-W=Æ, то пустое множество согласно определению 1 принадлежит . Если АÎ , то согласно определению 1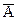 
= W-А также принадлежит . Таким образом, алгебра событий есть класс множеств замкнутый относительно операций сложения, умножения и дополнения.
Простейшим примером алгебры событий является множество, состоящее из двух элементов Æ и W. Легко проверить, что Á={Æ, W}- алгебра событий.
Если W конечное множество, то можно доказать, что множество всех его подмножеств является алгеброй событий.
Определение 2. Вероятностью называется числовая функция, определенная на некоторой s - алгебре . Каждому событию АÎÁ она ставит в соответствие число P(А). При этом должны выполняться следующие аксиомы:
1) Р(А) ³0 "АÎ ;
2) Р(W)=1;
3) Р(А+В)=Р(А)+Р(В), если АÎ , ВÎ , АВ=Æ;
4) Р(А)=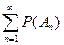 
, если А= 
и события Аn попарно несовместны.
Замечание. Если вероятность определена на алгебре , то аксиома 4 опускается. Совокупность (W, ,Р) называют вероятностным пространством.
В примере1 W={wi)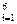 
. Множество всех подмножеств W будет алгеброй событий . Любое случайное событие АÎ можно записать так А={wi1, wi2, …, wik}. Событие А содержит k (0 £k £6) элементарных событий. При этом при k=0 A=Æ, при k=1 A= wi, при k=6 A=W. Событие В={w2, w4, w6}, например, означает выпадение четного числа очков. Здесь wi1=w2, wi2=w4, wi3=w6. Положим Р(А)=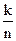 
где n=6. Можно убедиться (сделать это самостоятельно), что функция Р(А)= 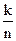удовлетворяет аксиомам 1-3 опр.2 и, следовательно, является вероятностью. При k=1 из Р(А)= получим Р(wi)=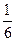 
, i=1, 2, …,6. Это означает, что все исходы опыта равновозможные. Поскольку каждое элементарное событие, входящее в А, является для него благоприятным, то формула Р(А)= 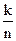совпадает с классическим определением вероятности .Используя Р(А)= 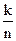, найдем Р(В)= 
= 
.
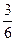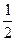Замечание. Система аксиом 1-3 определяет вероятность не однозначно. Действительно, выберем шесть чисел pi³0 так, чтобы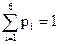 
, и событию А={wi1, wi2, …, wik} поставим в соответствие значение функции
Р(А)=рi1+ рi2+…+ рik
Можно убедиться, что функция Р(А)=рi1+ рi2+…+ рikудовлетворяет аксиомам 1-3 и опр. т.е. является вероятностью. Если р1=р2=…=р6= 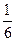, то функция Р(А)=рi1+ рi2+…+ рik совпадает с функцией Р(А)= 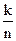. Если, например, р1=р2=…=р5=0, р6=1, то согласно Р(А)=рi1+ рi2+…+ рik Р(В)=р2+р4+р6=1. Видимое противоречие (ранее мы нашли Р(В)= 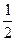) на самом деле таковым не является. Согласно Р(А)=рi1+ рi2+…+ рik Р(w1)=Р(w2)=…=Р(w5)=0, Р(w6)=1. Это означает, что исходы опыта теперь неравновероятны, что возможно, если кубик неправильный, несимметричный. Если, например, его склеить из плотной бумаги и на грань с одним очком наклеить свинцовую пластину, то при любом бросании противоположная грань с шестью очками будет верхней.
В пр. 3 W={x: x³0} – правая полуось системы координат. Элементарные события w={x: 0£x£w} являются отрезками этой полуоси. Если к ним добавить все разности этих отрезков (вычитать будем из большего меньший), то получим алгебру . Функцию Р(А) зададим интегралом Р(А)=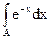 
Интегрирование в Р(А)= 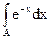производится по объединению всех отрезков, каковым является событие А. Можно убедиться что Р(А)= 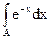является вероятностью. Пусть А={x: 1£x£2}, что можно толковать как отказ прибора между первым и вторым годом эксплуатации. Тогда Р(А)=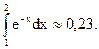 
В пр. 4 W={(x, y): x2+y2£r2}- круг радиуса r. Всякая область круга – случайное событие А. Элементарные события будем считать равновозможными. Однако, воспользоваться классическим определением вероятности нельзя, т.к. общее число событий и число благоприятных событий бесконечное. В этом случае используют так называемую геометрическую вероятность. Положим Р(А)= 
Здесь SA – площадь части круга, соответствующей событию А, а Sкр – площадь всей мишени. Можно доказать, что Р(А)= является вероятностью. В общем случае равновозможных исходов опыта геометрическая вероятность определяется формулой Р(А)=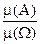 
Где m(А) – мера множества А. Если множество А конечное, то мера совпадает с числом его элементов, если А – отрезок, то мера совпадает с длиной отрезка, если А – часть плоскости – с площадью и т.д.
Рассмотрим теперь следствия из определения 2.
Следствие 1. Р(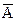 
)=1-Р(А)
Доказательство. Действительно, А+ 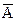=W, события А и 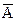несовместны, согласно аксиоме 3 Р(А)+ Р( 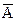)=1. Следствие доказано.
Следствие 2. (теорема сложения вероятностей).
Р(А+В)=Р(А)+Р(В)-Р(АВ)
Доказательство. Представим события А+В и В в виде суммы несовместных событий. А+В=А+В 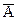(см. диаграмму Венна), В=В(А+ 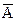)=ВА+В 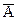. Воспользуемся аксиомой 3. Р(А+В)=Р(А)+Р(В 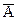), Р(В)=Р(ВА)+Р(В 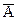). Подставляя выражение Р(В 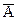) из второй формулы в первую, получим формулу. Следствие доказано. Теорема обобщается на сумму n событий.
… 
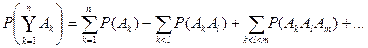Следствие 3. Если А=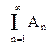 
и А1É А2 ÉА3 É…, то Р(А)= 
Дата добавления: 2021-01-21; просмотров: 95; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!