Общие сведения об инерциальных навигационных системах (ИНС)
ЛЕКЦИЯ 8 ИНЕРЦИАЛЬНЫЕ ИЗМЕРЕНИЯ
Основное уравнение инерциальной навигации
В инерциальной системе координат второй закон Ньютона записывается в форме
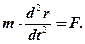
где r – геоцентрический радиус-вектор материальной точки массы m.
Необходимо учитывать, что на тело кроме механической силы действуют гравитационные силы. В задаче навигации в околоземном пространстве будем пренебрегать влиянием Солнца и планет Солнечной системы, также как нутационным и прецессионным движением Земли. Будем считать, что на тело кроме механической силы действует только гравитационная сила Земли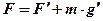 
. После подстановки в исходное уравнение и деления на m получим уравнение
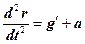, (8.1)
где g ¢- ускорение силы тяготения Земли,
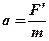- так называемое кажущееся ускорение. Это ускорение, которое имела бы материальная точка под воздействием негравитационных сил, если бы она могла двигаться в пространстве, свободном от действия сил тяготения.
Как показано в [1], именно кажущееся ускорение измеряет акселерометр. Векторную величину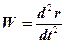 
называют абсолютным ускорением.
Возьмём геоцентрическую систему координат Ха Yа Zа, принимаемую за инерциальную, и систему координат XYZ, жестко связанную с Землёй. Системы расположим так, чтобы оси Zа и Z совпадали с полярной осью Земли. Введём систему координат x h z с произвольной ориентацией осей и вращающейся в инерциальном пространстве с угловой скоростью w.
Положение некоторой точки М в пространстве определяется геоцентрическим радиус-вектором r. Координаты конца радиус-вектора в различных системах координат описываются разными функциями времени. Производную, взятую в инерциальной системе Ха Yа Zа, называют полной и представляют как абсолютную скорость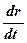 
=V.Производную во всех других подвижных системах координат называют локальной. Связь между полной 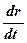и локальной 
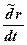производными определяется известным соотношением
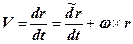. (8.2)
Локальная производная берётся в системе координат x h z, а w - абсолютная угловая скорость трёхгранника x h z. Абсолютное ускорение W определяется как вторая полная производная радиус-вектора r. Если учесть, что первая полная производная радиус-вектора rесть V, то
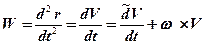. (8.3)
Векторное произведение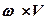 
на оси x, h, z получается развертыванием определителя
,
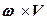
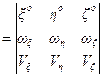где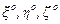 
- орты соответствующих осей.
Поэтому в проекциях на оси x, h, z будем иметь
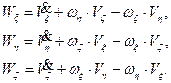(8.4)
Как известно, акселерометр измеряет кажущееся ускорение. С учётом уравнения (8.1) и (8.3) вектор кажущегося ускорения через абсолютную скорость представляется в виде
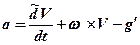. (8.5)
Это выражение представляет собой основное уравнение инерциальной навигации в абсолютных скоростях.
В координатной форме
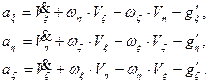(8.6)
Чтобы выразить абсолютное ускорение W через локальные производные радиус-вектора r, применим формулу полного дифференцирования к равенству (8.2)
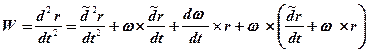
Производную, взятую в подвижной системе координат, представляют как относительную скорость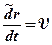 
. Поэтому
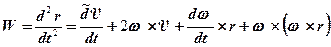. (8.7)
Первое слагаемое определяет относительное ускорение, второе – кориолисово ускорение, а два последних – переносное ускорение от вращательного движения координатной системы x h z в инерциальном пространстве.
В инерциальной навигации часто бывает удобно измерять кажущееся ускорение в системе координат x h z, вращающейся с абсолютной угловой скоростью w, а выражать абсолютное ускорение через проекции скорости относительно Земли в осях x, h, z. Для решения этой проблемы упрощение уравнения (8.7) будем вести в два этапа.
Применим формулу (8.7) для системы координат XYZ относительно опорной системы Ха Yа Zа. В этом случае угловая скорость равна скорости Земли w = W и Wx = Wy = 0; Wz = W = const. Отсюда
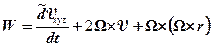. (8.8)
Далее рассмотрим две системы координат XYZ и x h z совместно. В этой паре опорной будем считать систему XYZ, а систему x h z будем считать вращающейся относительно XYZ с угловой скоростью wотн. Тогда получим
.
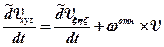Слева локальная производная в системе координат XYZ, а справа в системе координат x h z. Подставим это выражение в уравнение (8.8), получим
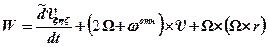. (8.9)
В дальнейшем локальную производную в системе координат x h z, которая вращается относительно Земли со скоростью wотн,для простоты будем представлять в виде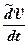 
или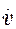 
. Из уравнений (8.9) и (8.1) вектор кажущегося ускорения представляется в виде:
.
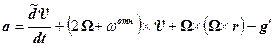По определению вектор ускорения силы тяжести g равен сумме гравитационного ускорения и центробежной силы от вращения Земли (раздел 3)
.
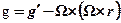Поэтому уравнение для кажущегося ускорения можно записать в виде
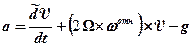. (8.10)
В координатной форме
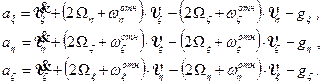(8.11)
Общие сведения об инерциальных навигационных системах (ИНС)
В 1923 году австрийский ученый Шулер сформулировал теорию о том, что если настроить математический маятник, длина которого от точки подвеса до колеблющейся материальной точки равна радиусу Земли, то ускорение по касательной к поверхности Земли не заставит нить маятника отклоняться от радиуса, проведённого от точки к центру Земли. Период собственных колебаний такого маятника составляет 84.4 минуты. Расчёты показали, что физический маятник с таким периодом в приемлемых габаритах должен иметь столь малое плечо, что практически не может быть реализован. Однако оказалось возможным создание гироскопических устройств, моделирующих поведение маятника с таким периодом.
Сущность ИНС состоит в следующем. Ускорения, действующие на систему, измеряются чувствительными элементами – акселерометрами. Обычно акселерометры устанавливаются на гиростабилизируемую платформу, которая до перевода в рабочий режим выставляется в горизонтальную плоскость. Измеренные ускорения интегрируются и получаются линейные скорости. Моделирование маятника Шулера достигается тем, что на датчики моментов гироскопов гиростабилизированной платформы подаётся сигнал, пропорциональный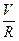 
, где R – радиус кривизны земной поверхности. В результате гироплатформа развернётся на угол, равный 
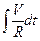и сохранит своё горизонтальное положение относительно Земли. Проблема заключается в том, чтобы выделить из показаний акселерометра производную скорости и при подаче сигнала на датчики моментов гироскопов учесть несферичность Земли.
Инерциальные системы с таким построением называются системами полуаналитического типа.
Для полноты картины следует упомянуть о ИНС, в которых гиростабилизированная платформа после перевода в рабочий режим неподвижна в инерциальном пространстве. А вертикаль к поверхности Земли определяется расчетным путём. Такие ИНС относят к системам аналитического типа.
ИНС могут быть созданы и без использования гиростабилизированной платформы. Это так называемые бесплатформенные инерциальные навигационные системы (БИНС). В таких системах чувствительные элементы жестко закреплены по строительным осям изделия. Горизонт в таких системах определяется расчётным путём.
Дата добавления: 2021-01-21; просмотров: 532; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!